[R-Machine Learning] 8. 서포트 벡터 머신 (SVM)

1. 서포트 벡터 머신(SVM)

1) 마진(Margin) & 서포트 벡터(Support Vector)

• 서포트 벡터 머신에 대해 설명하기 위해서는 우선 마진과 서포트 벡터에 대해서 알아야 한다.

• 마진(Margin)

  • 클래스를 구분하는 초평면과 가장 가까운 훈련샘플 사이의 거리를 의미한다. 즉, 속성 값에 따라 다차원 공간의 예제를 여러가지 점 간의 경계를 정의하는 평면으로 볼 수 있다.
    

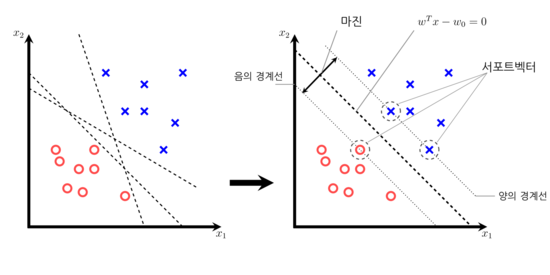
• 서포트 벡터 머신은 위에서 언급한 마진을 최대화하는 방향으로 최적화를 진행한다. 그 이유는 마진이 클 수록 일반화 오차가 낮아지기 때문이다.
  따라서 마진이 클 수록 좋은 성능을 내는데 이 때 마진의 경계에 걸치는 샘플들을 서포트 벡터라고 한다.
  

2) 서포트 벡터 머신의 이해

• 위의 내용을 통해 서포트 벡터 머신을 “마진을 최대화하는 분류 경계면을 찾는 기법” 이라고 할 수 있다. 따라서 초평면이라는 한쪽 면으로 동일한 데이터가 놓이게 평평한 경계를 만드는 것이 목적이라고 할 수 있다.
• 전형적으로 적용하는 이진 분류에 사용하는 것이 좋다.

(1) 최대 마진 찾기

• 마진을 최대화 하는 방법에 대해서 알아보자. 예를 들어 아래 그림과 같이 데이터가 분포한다고 가정하고 이를 2분류로 나눌 수 있는 직선이 그림의 3개 직선이라고 가정해보자.

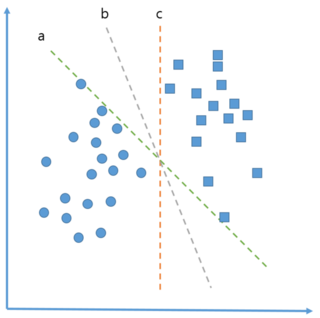
• 위의 3개 직선 중 어떤 직선을 선택하더라도 모든 데이터 점들이 2분류 되지만, 임의의 데이터에 대해서도 최대한 일반화하게 구별할 수 있는 직선이어야한다.
  또한 위의 그림에서 보여지는 것처럼 경계선 주변에 있는 점들이 약간 변동됨으로써 우연히 직선에 걸치거나 넘게되는 점들이 생길 수 있다.
• 예를 들어 a 직선을 선택한다고 가정하고 최대 간격이 아래 그림에서의 빨간색 직선만큼이라면 빨간색 직선위에 걸치게 되는 점들이 서포트 벡터가 되며, 각 범주는 하나 이상 서포트 벡터를 가지고 있어야한다.

(2) 선형적으로 구별 가능한 데이터인 경우

• 범주를 선형적으로 구별할 수 있다고 가정할 때, 최대 마진 초평면은 2개 그룹에 속한 데이터들 중 최외곽에 위치한 데이터들 중에서 가장 가까운 거리를 계산해 이를 직각 이등분하는 직선이라고 할 수 있다.

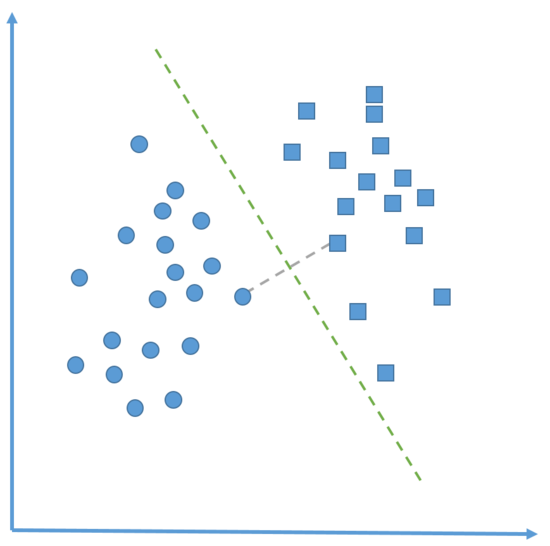
• 위의 내용을 수식으로 풀어보자면, 다음과 같이 진행된다. 우선 n차 공간에서의 초평면은 아래와 같이 정의할 수 있다.
  $ \vec{w} \cdot \vec{x} + b = 0 $
  
  

• w는 n개 가중치 벡터를 의미하며, b는 편향을, x는 입력 벡터를 의미한다. 위의 공식을 사용해 아래와 같이 두 초평면을 명시하는 가중치 w를 찾는 것이 목적이다.
  $ \vec{w} \cdot \vec{x} + b \geq 1 $
  $ \vec{w} \cdot \vec{x} + b \leq -1 $
  

• 첫 번째 초평면보다 위쪽으로 놓여야되고, 두번째 초평면보다 아래쪽으로 분포하도록 2개 그룹으로 나눠져야 한다.
• 표현식에 의해 모든 데이터는 선형적으로 구별되어야한다.

• 벡터 기하학에서는 두 평면 사이의 거리를 계산할 때 아래와 같이 정의한다.
  $ d = \frac {2} {\Vert \vec{w} \Vert} $
  

• 위의 식에서 $\Vert \vec{w} \Vert$ 는 유클리드 정규를 의미하며, 최대마진을 구하기 위해 w를 최소화할 필요가 있다. 제약사항에 대해서는 아래와 같이 표기한다.
  $ min \frac {1} {2} {\Vert \vec{w} \Vert}^2 $
  
  $ s.t. y_i ( \vec{w} \cdot \vec{x_i} - b ) \geq 1, \forall \vec{x_i} $
  
  

• 위의 공식에서 s.t. 은 올바르게 분류된 y 데이터 점의 각 조건을 최소화 한다는 의미이다. y 는 분류값(+1 또는 -1로 변환)을 나타내고, $\forall$ 는 “모든”이라는 의미이다.

(3) 비선형적으로 구별 가능한 데이터의 경우

• 앞서 살펴본 것처럼 SVM은 선형적인 경우에 구별하는 것이 쉽다고 알 수 있다.

• 하지만 아래의 예시처럼 선형적으로 나누게 되면 모든 데이터를 100% 완벽하게 분류하는 경우는 드물며, 오히려 소수의 데이터에 대해서는 오분류를 할 수 있다.
  이럴 경우 SVM에 잘못된 범주에 속하는 일부 점의 거리인 소프트 마진을 만드는 “여유변수” 라는 것을 추가해주면 해결할 수 있다.

• 예를 들어 아래 그림과 같이 데이터가 분포하고 선형 경계를 생성했다고 가정해보자.

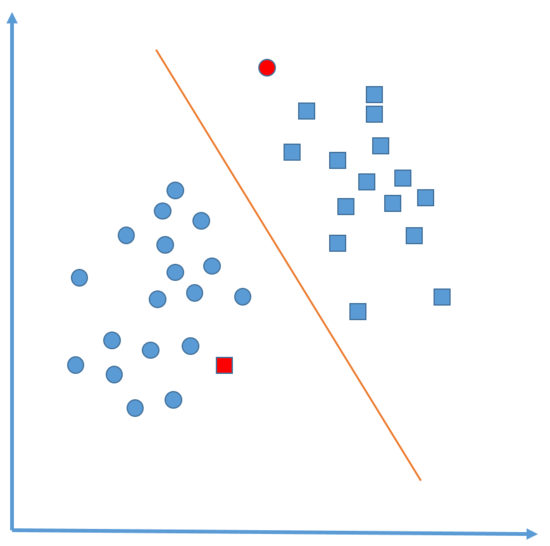
• 위의 그림에서 빨간색으로 칠한 부분은 해당 선형 경계가 잘못 분류한 부분이며, 위와 같은 경우 비용값을 사용해 최적화 문제를 변환한다.

• 비용 값(Cost Value) 란 잘못 속해 있는 모든 점에 적용하고, 최대 마진을 찾는 것이 아닌, 알고리즘의 총 비용 값을 최소화하려는 값을 의미한다.
  따라서 최적화에 대한 표현식은 아래와 같이 변형된다.
  $ min \frac {1} {2} {\Vert \vec{w} \Vert}^2 + C \sum_{i=1}^{n} \xi_i $
  
  $ s.t. y_i( \vec{w} \cdot \vec{x_i} - b ) \geq 1 - \xi_i , \forall \vec{x_i} , \xi \geq 0 $
  

• 위의 수식에서 중요한 부분은 비용 매개변수인 C가 추가되었다는 점이다.
• 값의 변경에 따라 다른 초평면으로 잘못 속해 있는 예제들이 패널티를 조절하며, 비용 매개변수의 값이 클 수록 최적화는 어려워지고 100% 구별을 하려고 한다.
• 반면, 비용 매개변수의 값이 작아지면 전체적인 마진을 넓게 한다.

3) 비선형 공간에서의 커널 사용

• 앞서 살펴본 것처럼 SVM은 선형적인 경우에 구별하는 것이 쉽다고 알 수 있다. 하지만 일반적인 문제들은 대부분 비선형적으로 경계를 나눠야 구분이 가능하다.
  즉, 변수간의 관계가 비선형적이라고 할 수 있는데, SVM에서는 일부 예제의 잘못된 분류를 용인하는 비용매개변수를 추가하는 것 뿐만 아니라 커널 방법으로 알려진 과정을 사용해 문제를 고차원 공간으로 적용할 수 있다.

• 커널(Kernel)
  • 커널이란 주어진 데이터를 고차원 특징 공간으로 매핑시켜준다. 고차원 공간에 매핑되면, 원래 차원에서는 보이지 않던 선형으로 분류할 수 있는 방법을 찾을 수 있다.
    때문에 2차원 공간에서 분류 불가능한 것이 3차원 공간으로 매핑된다면 명확하게 분류할 수 있는 가능성이 높아진다.

• 비선형 커널 SVM은 구별을 만들어주기 위해 데이터에 부가적인 차원을 추가하게 된다. 본질적으로 커널 기법은 측정된 속성 간의 수학적인 관계를 나타내는 새로운 속성을 추가하는 과정과 관련된다.

• 비선형 커널 SVM 기법의 장단점은 다음과 같다.
  

장점	단점
범주나 수치 예측 문제에 대해 사용할 수 있다.	최적의 모델을 찾기 위해 커널과 모델에서 매개변수의 여러가지 조합 테스트가 필요하다.
노이즈 데이터에 영향을 크게 받지 않고 잘 과적합되지 않는다.	특히 잘 지원되는 일부 SVM 알고리즘 때문에신경망보다 사용하기 쉽다.
특히 입력 데이터 셋이 예제 개수와 속성의 수가 많다면 훈련이 느릴 수 있다.	해석하기 불가능하지 않으나, 어렵고 복잡한 블랙박스를 만든다.

• R에서 사용할 수 있는 커널은 다음과 같다.

① 선형 커널

• 데이터를 전혀 변환하지 않으며, 단순히 속성의 내적으로 나타낸다.
  $ K( \vec{x_i}, \vec{y_j} ) = \vec{x_i} \cdot \vec{y_j} $

② 차수 다항 커널

• 데이터의 비선형 변환에 추가한다.
  $ K( \vec{x_i}, \vec{y_j} ) = {(\vec{x_i} \cdot \vec{y_j} + 1)}^d $

③ 시그모이드 커널

• SVM 모델은 시그모이드 활성 함수를 사용한 신경망과 조금 유사하다. 식에서 사용된 카파와 델타는 커널 매개변수를 사용한다.
  $ K( \vec{x_i}, \vec{y_j} ) = tanh(k \vec{x_i} \cdot \vec{y_j} - \delta) #

④ 가우시안 RBF 커널

• RBF 커널은 다양한 데이터의 형태에 잘 적용되기 때문에 많은 학습 태스크의 합리적이다.
  $ K( \vec{x_i}, \vec{y_j} ) = e \frac {2 {\sigma}^2 } {- { \Vert \vec{x_i} - \vec{x_j} \Vert }^2 } $

• 어떤 커널을 사용할 지 결정하는 합리적인 규칙은 없다. 적합화는 학습할 개념뿐만 아니라 훈련 데이터의 총량, 속성 간의 관계와 매우 관련이 높다.
• 따라서 시도와 오차는 검증된 데이터 셋에서 훈련과 평가가 필요하다. 대부분의 경우 성능은 차이가 크지 않기 때문에 커널의 선택은 임의적이다.

2. SVM 실습 : OCR 수행하기

• 이미지 처리는 머신러닝으로 해결하는 여러 태스크 중 가장 어려운 태스크에 해당한다.
• 높은 개념에 화소의 연결 패턴 관계는 매우 복잡하고 정의하기 어렵다. 더욱이 이미지 데이터는 노이즈에 영향을 많이 받는다.

• 때문에 SVM을 사용할 경우, 노이즈에 민감하지 않도록 복잡한 패턴을 학습할 수 있으며, 높은 정확도로 시각 패턴을 인식할 수도 있다.

• 이번 실습은 상형문자들에 대해 인식하고 분류해내는 실습을 진행할 것이다.
• 사용할 데이터는 UCI Machine Learning Data Repository 에 기부한 데이터 셋을 사용한다.

1) 데이터 수집

• OCR 소프트웨어가 문서를 처리할 때는 문서를 격자의 각 칸과 같은 매트릭스로 나눈다.
• 각 칸에서 소프트웨어는 인식가능한 모든 문자들을 매칭하는 작업을 진행한다.
• 사용하려는 문서는 A 부터 Z 까지 26개의 영어 알파벳 대문자 20,000개의 예제를 포함한다.

2) 데이터 준비와 탐구

• 문자를 컴퓨터로 스캔할 때 펙셀을 16개의 통계속성으로 변형하며, 이번 예제에서 사용할 데이터 셋이기도하다.
• 사용할 속성은 다음과 같다.
• 문자의 수직 픽셀 비율
• 문자의 수평 픽셀 비율
• 문자의 검정 픽셀 비율

• 픽셀의 수평, 수직의 위치의 평균

• SVM의 특징 중 하나로, 모든 속성은 수치여야하고, 각 속성은 작은 간격 범위로 되어있어야 한다.

 [R Code]
 
 data <- read.csv("Data/letterdata.csv", header=T)
 str(data)

[실행 결과]

str(data)
'data.frame': 20000 obs. of 17 variables:
$ letter: Factor w/ 26 levels "A","B","C","D",..: 20 9 4 14 7 19 2 1 10 13 ...
$ xbox : int 2 5 4 7 2 4 4 1 2 11 ...
$ ybox : int 8 12 11 11 1 11 2 1 2 15 ...
$ width : int 3 3 6 6 3 5 5 3 4 13 ...
$ height: int 5 7 8 6 1 8 4 2 4 9 ...
$ onpix : int 1 2 6 3 1 3 4 1 2 7 ...
$ xbar : int 8 10 10 5 8 8 8 8 10 13 ...
$ ybar : int 13 5 6 9 6 8 7 2 6 2 ...
$ x2bar : int 0 5 2 4 6 6 6 2 2 6 ...
$ y2bar : int 6 4 6 6 6 9 6 2 6 2 ...
$ xybar : int 6 13 10 4 6 5 7 8 12 12 ...
$ x2ybar: int 10 3 3 4 5 6 6 2 4 1 ...
$ xy2bar: int 8 9 7 10 9 6 6 8 8 9 ...
$ xedge : int 0 2 3 6 1 0 2 1 1 8 ...
$ xedgey: int 8 8 7 10 7 8 8 6 6 1 ...
$ yedge : int 0 4 3 2 5 9 7 2 1 1 ...
$ yedgex: int 8 10 9 8 10 7 10 7 7 8 ...

• 데이터의 구조를 확인해본 결과 모든 값이 상수로 구성되어 있기 때문에 팩터를 수치로 변환할 필요는 없다. 하지만, 일부 값이 꽤 넓은 범위로 되어있으며, 정규화나 표준화를 해줘야 한다.
• 위의 데이터 중 80%는 학습용 데이터로, 20%는 테스트용 데이터로 분할한다.

[R Code]

train <- data[1:16000,]
test <- data[16001:20000,]

3) 모델링

• R 에서 SVM 모델을 사용할 때, e1071 패키지를 많이 이용하지만, 이번 예제에서는 kernlab 패키지를 사용한다.

• 기존에 만들어진 패키지들은 대부분 C, C++ 로 짜여진데 반해, 해당 패키지는 R로 개발되었다. 때문에 쉽게 변경이 가능하고, 여러 자동화된 기법을 사용해 훈련하고 평가할 수 있다.

• kernlab에서 SVM 모델을 만들려면 ksvm() 함수를 사용하면되며, 사용방법은 다음과 같다.

[R Code]

m <- ksvm(target ~ predictors, data = mydata, kernel = 'rbfdot', C=1)
# target : 결과 변수
# predictors : 예측 변수
# data : 사용 데이터
# kernel : 사용할 커널, rbfdot(radial basis), polydot(polynomial), tanhdot(hyperbolic tangentsigmoid), vanilladot(linear) 중 하나를 입력
# C : 제약 위반에 대한 비용을 명시하며, soft margin에 대한 벌칙 크기보다 큰 값일 경우 여백을 작게 만든다.

[R code]

model_ksvm <- ksvm(letter ~ ., data=train, kernel="vanilladot")

• 모델에 대한 정보를 출력해보면 다음과 같이 나온다.

[R code]

model_ksvm

[실행결과]

Support Vector Machine object of class "ksvm"

SV type: C-svc (classification)
parameter : cost C = 1

Linear (vanilla) kernel function.

Number of Support Vectors : 7037

Objective Function Value : -14.1746 -20.0072 -23.5628 -6.2009 -7.5524 -32.7694 -49.9786 -18.1824 -62.1111 ...
Training error : 0.130062

4) 성능 평가

• 출력된 결과를 통해서 알 수 있듯이, 모델이 얼마나 잘 수행 됬는지에 대한 정보는 Training error 외에는 확인할 방법이 없다.
  따라서 일반화가 잘 됐는지 확인하기 위해 테스트용 데이터를 이용해 예측을 해보자

[R code]

y_pred_ksvm <- predict(model_ksvm, test)
head(y_pred_ksvm)

[실행결과]

[1] U N V X N H
Levels: A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

• 추가적으로 분류기가 예측한 문자와 실제 문자가 얼마나 일치하는 지 갯수로 확인해보자.

[R Code]

table(y_pred_ksvm, test$letter)

[실행결과]

• 위의 결과에서 대각선에 위치한 숫자들은 제대로 예측한 경우의 수이고, 그 외의 위치에 있는 숫자들은 잘못 예측한 경우의 수라고 할 수 있다.
• 하지만 여전히 얼마나 잘 맞았는지 확인이 어렵기 때문에 분류 성공 여부를 비율로 나타내보자.

[R Code]

performance_ksvm <- y_pred_ksvm==test$letter
table(performance_ksvm)
prop.table(table(performance_ksvm))

[실행 결과]
performance_ksvm
FALSE TRUE
643 3357

performance_ksvm
FALSE TRUE
0.16075 0.83925

• 선형 커널 함수로 커널을 설정할 경우 약 80%의 정확도를 갖는 것으로 확인된다.

5) 모델 성능 향상

• 이번에는 선형 커널 함수가 아닌, 좀 더 복잡한 커널 함수를 사용했을 때 성능이 향상되는지를 확인해보자.
• 좀 더 복잡한 커널 함수를 사용할 경우, 데이터를 높은 차원 공간으로 연결할 수 있고, 더 적합한 모델을 얻을 수 있다.
• 이번 예제에서는 가우시안 RBF 커널 함수를 사용하며, 과정은 이전에 선형 커널 함수로 진행한 과정과 동일하다.

[R code]

model_ksvm <- ksvm(letter ~ ., data=train, kernel="rbfdot")
y_pred_ksvm <- predict(model_ksvm, test)

performance_ksvm <- y_pred_ksvm==test$letter
table(performance_ksvm)
prop.table(table(performance_ksvm))

[실행 결과]

performance_ksvm
FALSE TRUE
277 3723

performance_ksvm
FALSE TRUE
0.06925 0.93075

• 실행 결과를 비교해보면, 가우시안 RBF 커널 함수를 사용했을 때가 93%로 성능 향상이 된 것을 확인할 수 있다.
• 만약 추가적으로 성능을 높이고 싶다면, 결정 경계선인 C의 값을 변경해주면 된다.