[R-Machine Learning] 7. 인공신경망

1. 인공신경망

• 생물적으로 뇌가 감각 입력의 자극에 어떻게 반응하는지에 대한 이해로부터 얻어진 모델로, 입력 신호와 출력 신호 간의 관계를 모델화한다.
• 인간 뇌 행동의 개념적인 모델로서, 의도적으로 디자인됐기 때문에 뉴런이 어떤 역할을 하는지에 대한 이해가 필요하다.
• 일반적으로 뉴런은 아래 그림과 같이 생겼으며 입력신호는 상대적인 중요도나 빈도에 따라 가중치가 부여된다.

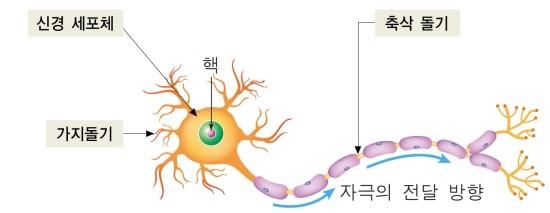
• 위와 같은 생화학적 과정을 통해 세포의 가지 돌기로 받아들인후 몸체에서 입력된 신호를 축척해 경계 값에 도달하면 출력신호를 전기 화학적으로 축색돌기에 전달한다.
• 마지막으로 축색돌기 의 말단에서 화학적 신호로 처리된 전기 신호는 다시 스냅스로 알려진 작은 간극을 통해 다른 뉴런에게 전달한다.
  
  
• 인공신경망 역시 위의 과정을 모델화 한 것이기 때문에 과정은 유사하다.
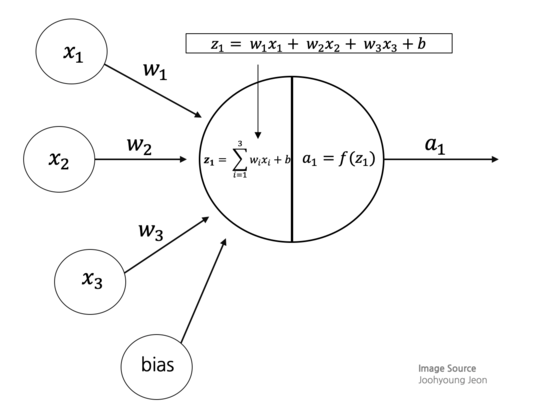
• 아래 그림에 묘사된 것처럼 방향성 네트워크 다이어그램으로 구성되었으며 가지 돌기에서 받은 입력 신호와 결과신호 간의 관계를 정의한다.
• 각 가지 돌기의 신호는 중요도에 따라 가중치를 부여받는다. 입력 신호는 세포 몸체에서 합해지고, 신호를 f로 표기된 활성 함수에 따라 신호가 전달된다.
• 활성 함수로 신호가 전달되면 적용된 함수에 의해 출력 신호가 반환된다.

1) 활성 함수

• 인공뉴런이 정보를 처리하거나 망 전체로 전달하는 일종의 동작이라고 볼 수 있다.
• 생물에 빗대어 표현하자면, 입력받은 모든 신호를 더해 종합적으로 어떠한 행동 혹은 판단을 하는 과정이라고 볼 수 있다.
• 단순히 명시된 입력 경계값에 도달하면 출력신호를 만든다고하여 경계 활성 함수라고도 한다.
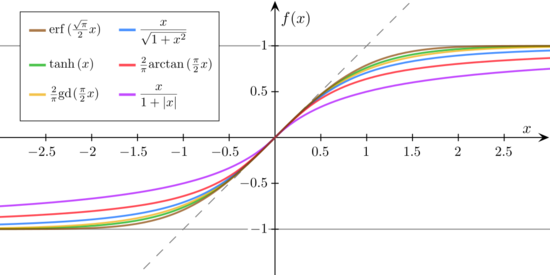
• 주로 사용되는 함수는 시그모이드 함수 계열이 많이 사용된다.
• 시그모이드 함수의 경우 미분 가능하고 입력 전체 범위에 걸쳐 도함수를 계산할 수 있다.
• 주요 함수들은 아래의 그림과 같다.

2) 신경망 구성

• 신경망의 구조는 종류에 따라 제각각이지만, 공통적인 특징 3가지가 있다.
  • 층의 개수
  • 정보가 뒷단으로 전달될 수 있는지
  • 각 층 내에 있는 노드의 개수
• 신경망이 학습해야 할 테스크의 복잡성에 따라 토폴로지가 좌우된다.
• 또한 네트워크가 복잡한 경우에는 미묘한 패턴을 잘 식별할 줄 알고, 복잡한 결정경계를 식별할 줄 아는 능력이 필요하며 이는 노드의 배열에 의존적인 경우가 크다.

(1) 층의 개수

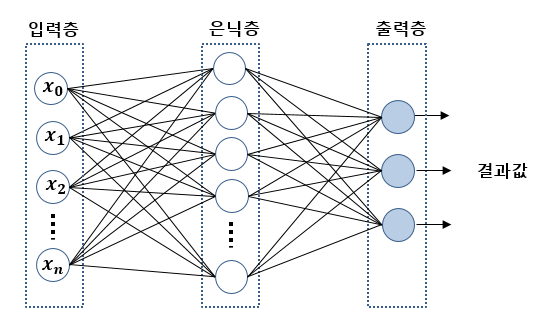
• 일반적인 신경망은 크게 3개의 층으로 구성된다.
  • 입력층 : 가공되지 않은 신호를 받아, 데이터 셋에서 하나의 속성을 처리하는 일을 담당한다.
  • 은닉층 : 출력 되기 전에 입력 노드에서 전달받은 신호를 처리하는 층으로 일반적인 경우 하나 이상의 은닉층을 추가한다.
  • 출력층 : 은닉층에서 받은 신호를 활성함수의 입력으로 하여 최종적인 결과를 산출한다.

(2) 정보의 진행 방향

• 위의 그림을 통해서도 알 수 있겠지만 입력층 ~ 출력층으로 신호가 전달된다는 것을 알 수 있다. 이와 같이 한쪽으로 진행되는 구조를 전방향(Feed Forward) 라고 한다.
• 전방향으로 신호가 전달되면 정보의 흐름에 대한 제한에도 상관 없을 만큼 유연성을 가지게 된다.
• 각 층의 개수와 노드 수를 변경해 다중 결과를 동시에 모델화하거나 다중 은닉층을 적용할 수도 있다.

(3) 각 층의 노드 수

• 층의 개수, 정보의 진행방향과 더불어서, 각 층의 노드 개수에 따라 신경망의 복잡성이 증가한다.
• 입력 노드의 개수는 입력 데이터의 속성 수로 결정되며 출력 노드의 수는 결과의 분류 개수나 모델의 결과 수에 의해 결정된다. 마지막으로 은닉 노드의 경우 모델 훈련에 앞서 미리 정의하고 학습을 수행하게 된다.
• 특히 은닉층의 경우에는 특별한 룰이 없어, 적당한 개수는 입력 노드의 수, 훈련 데이터 수, 노이즈가 있는 데이터의 양, 파라미터 값, 학습 태스크의 복잡성을 모두 고려해서 결정해야된다.
• 또한 뉴런의 개수가 많으면 일반적으로 훈련 뎅이터를 반영하는 모델을 만들 수 있겠지만, 과대적합의 가능성 역시 높아지며, 훈련 속도 자체가 느린 편이다.

3) 역전파(Back Propagation)

• 다른 머신러닝 알고리즘들 보다 상대적으로 느린 편이지만, 학습에 있어 다른 모델들 보다 높은 정확도를 갖도록 하는 주요 기술이라고 할 수 있다.

• 이에 대해 장점과 단점은 아래의 내용과 같다.

장점	단점
분류, 수치 예측문제에서 사용될 수 있다.	망이 복잡해지는 경우, 훈련속도가 느리다.
가장 정확한 모델링 접근법 중 하나다.	훈련 데이터에 과대/과소적합되기 쉽다.
데이터 내에 주요 관계에 대한 몇가지 가정을 만든다.	해석하기 불가능하지 않으나, 다소 복잡한 블랙박스가 된다.

• 가장 일반적인 역전파 알고리즘은 크게 2개 과정에서 많은 순환을 반복한다.

  • 전방향 (Forward Phase)
    입력 층 ~ 출력 층으로 순서대로 활성화되고, 각 뉴런의 가중치와 활성 함수가 적용되어 출력신호를 생성한다.

  • 역방향 (Backward Phase)
    전방향에서 생성된 결과 신호를 훈련 데이터의 실제 목표 값과 비교하여, 출력 신호와 실제 값 사이의 차이를 이용해 뉴런 간의 연결 가중치를 변경하고, 미래의 오차를 줄이기 위해 역방향으로 전파되는 오차를 생성한다.

• 위의 2개 과정을 통해 모델은 학습률로 알려진 최대한 오차를 줄이는 방향으로 학습이 되며, 결과적으로 망 전체의 오차를 줄이며, 경사 하강법과 함께 적용되어 훈련을 빠르게 진행하도록 한다.

2. 실습 : 콘크리드 내구력 모델화

• 실습의 목적은 최종 생산물의 내구력을 정확하게 평가하기 어려운 만큼 입력 재료의 구성 목록을 이용해 실제 현장을 좀 더 안전하게 만들 수 있는 콘크리트의 내구력을 구성하는 요소를 예측하는 것이다.

1) 데이터 로드 및 탐색

• 데이터는 총 1,030 개의 예제를 포함하고 있으며, 구성 요소로는 총 8개의 속성으로 되어 있다.

[R Code]
data <- read.csv("Data/concrete.csv")
str(data)

'data.frame': 1030 obs. of 9 variables:
$ cement : num 141 169 250 266 155 ...
$ slag : num 212 42.2 0 114 183.4 ...
$ ash : num 0 124.3 95.7 0 0 ...
$ water : num 204 158 187 228 193 ...
$ superplastic: num 0 10.8 5.5 0 9.1 0 0 6.4 0 9 ...
$ coarseagg : num 972 1081 957 932 1047 ...
$ fineagg : num 748 796 861 670 697 ...
$ age : int 28 14 28 28 28 90 7 56 28 28 ...
$ strength : num 29.9 23.5 29.2 45.9 18.3 ...

• 구성 요소에 대한 설명은 다음과 같다.

  cement : 시멘트 총량
  slag : 슬라그 량
  ash : 화분 (재) 량
  water : 물 양
  superplasticizer : 고성능 감수제
  coarse aggregate : 굵은 골제
  fine aggregate : 잔 골제
  age : 숙성 시간
  strength : 콘크리트 강도

• 추가적으로 위의 데이터 구조를 통해서 본 결과 각 변수에 대한 값이 제각각으로 분포되어 있다는 것을 알 수 있다. 좀 더 확실하게 알기 위해 아래와 같이 summary 를 통해 분포를 확인해보자.

[R Code]

summary(data)

cement slag ash
Min. :102.0 Min. : 0.0 Min. : 0.00
1st Qu.:192.4 1st Qu.: 0.0 1st Qu.: 0.00
Median :272.9 Median : 22.0 Median : 0.00
Mean :281.2 Mean : 73.9 Mean : 54.19
3rd Qu.:350.0 3rd Qu.:142.9 3rd Qu.:118.30
Max. :540.0 Max. :359.4 Max. :200.10

water superplastic coarseagg
Min. :121.8 Min. : 0.000 Min. : 801.0
1st Qu.:164.9 1st Qu.: 0.000 1st Qu.: 932.0
Median :185.0 Median : 6.400 Median : 968.0
Mean :181.6 Mean : 6.205 Mean : 972.9
3rd Qu.:192.0 3rd Qu.:10.200 3rd Qu.:1029.4
Max. :247.0 Max. :32.200 Max. :1145.0

fineagg age strength
Min. :594.0 Min. : 1.00 Min. : 2.33
1st Qu.:731.0 1st Qu.: 7.00 1st Qu.:23.71
Median :779.5 Median : 28.00 Median :34.45
Mean :773.6 Mean : 45.66 Mean :35.82
3rd Qu.:824.0 3rd Qu.: 56.00 3rd Qu.:46.13
Max. :992.6 Max. :365.00 Max. :82.60

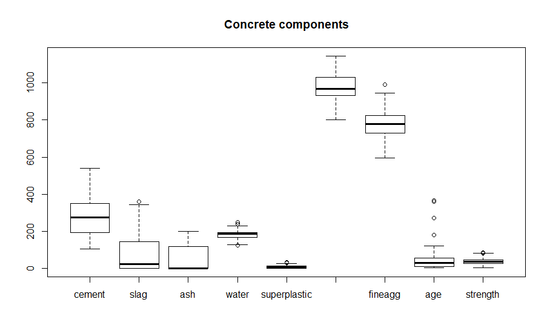
• 위의 2개 결과를 보면 알 수 있듯이, 변수의 값이 0 ~ 수천까지 형성돼 있다.
• 이를 위해 정규화와 표준화를 적용하여, 모든 값을 0 ~ 1 사이의 값으로 변경한다.

[R Code]

normalize <- function(x) {
    return( (x - min(x)) / (max(x) - min(x)))
}

concrete_norm <- as.data.frame(lapply(data, normalize))
boxplot(concrete_norm, main="Concrete components applied norm")

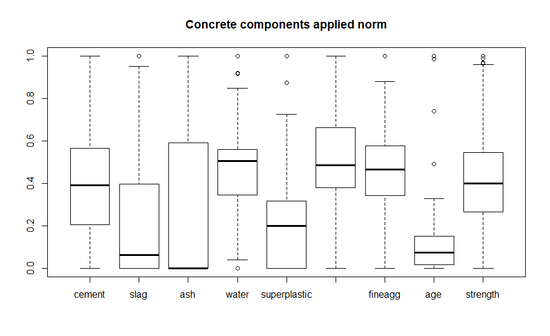
• 다음으로 할 일은 모델을 생성하기 전에 데이터를 학습용 데이터와 테스트용 데이터로 분류하는 일이다. 아이쳉 예의 논문에 따라 전체 데이터의 75%를 학습용으로, 나머지 25%은 테스트용으로 사용한다.

[R Code]

train <- concrete_norm[1:773, ]
test <- concrete_norm[774:1030, ]

2) 데이터 모델 훈련

• R 에서 신경망을 생성하려면, nnet 혹은 neuralnet 패키지 중 하나를 사용한다.
• 이번 예제에서는 neuralnet 패키지를 사용하여 모델을 생성한다.
• neuralnet 패키지의 neuralnet() 함수를 사용해 모델을 생성하며, 함수의 파라미터는 다음과 같다.

[R Code]
neuralnet(target ~ predictors, data = myData, hideen= 1, threshold=1, rep=1, startweight,
    algorithm = "rprop+" , err.fct = "sse", act.fct = "logistic", linear.output=FALSE,
... )

# target : 모델링에 사용되는 목적 변수
# predictors : 예측에 사용하는 데이터 프레임의 속성(입력 변수)
# data : target 과 predictors 가 포함되어 있는 데이터 (입력 혹은 훈련 데이터)
# hidden : 은닉층의 뉴런 수를 의미함, 기본값은 1
# threshold : 중단 기준으로 에러 함수의 편미분 값을 의미함, 기본값은 0.01
# rep : 훈련 반복횟수를 의미함, 기본값은 1
# startweights : 초기 가중치 값을 의미함, 기본값은 표준 정규분포의 무작위 수로 입력됨
# algorithm : 알고리즘 타입을 의미함, "backprop", "rprop+", "rprop-", "sag", "slr" 중 하나를 입력, 기본값은 "rprop+"를 사용함
# err.fct : 미분 오차함수를 의미함, "sse"(제곱합 에러), "ce"(교차 엔트로피) 중 하나를 사용함, 기본값은 "sse"
# act.fct : 미분 활성화 함수를 의미함, "logistic", "tanh" 중 하나를 입력함, 기본값은 "logistic"
# linear.output : 논리값으로 act.fct가 출력뉴런에 적용되지 않으면 TRUE를 입력함, 기본값은 FALSE

• 실습 데이터로 모델을 생성하려면 다음과 같다.

[R Code]

model <- neuralnet(strength ~ . , data = train)

• 위의 코드는 단순히 모델을 생성한 것뿐이다. 따라서 학습을 하기 위해서는 compute() 함수를 사용해야 하며, 방법은 다음과 같다.

[R Code]

compute(model, test[, -target])

# model : neuralnet() 함수를 이용해 생성한 모델
# test[, - target] : 테스트용 데이터로 [, - target] 의 의미는 테스트 셋에 target 변수가 속한 경우를 감안해 표현한 것으로, target 변수를 제외한 나머지 변수
#                    (정확히는 모델 생성시 사용된 변수) 를 사용하라는 의미이다.

• 실습을 예로 학습을 진행하면 다음과 같다.

[R Code]

result <- compute(model, test[1:8])

• 이 때 변수 result 는 학습에 대한 결과가 담긴 변수로 리스트 형식의 값을 가진다.
• 요소는 neurons 와 net.result 라는 값을 갖는다.
• neurons 는 테스트 셋을 적용했을 때 각 층에 존재하는 뉴런의 출력값을 의미한다.
• net.result 는 테스트 셋에 대한 예측 결과를 담고 있다.

[R Code]
length(result$neurons)
print(result$neurons[0])
print(result$neurons[1])

[실행 결과]

2

list()

[[1]]
cement slag ash water
774 1 0.68036530 0.00000000 0.0000000 0.52076677
775 1 0.25251142 0.00000000 0.5017491 0.30031949
776 1 0.39497717 0.00000000 0.0000000 0.48881789
777 1 1.00000000 0.00000000 0.0000000 0.40894569
778 1 0.62557078 0.00000000 0.0000000 0.74121406
779 1 0.48401826 0.00000000 0.5647176 0.38498403
780 1 0.44748858 0.00000000 0.5347326 0.33706070
781 1 0.34109589 0.00000000 0.5912044 0.56789137
782 1 0.44292237 0.00000000 0.5332334 0.79552716
783 1 0.34109589 0.00000000 0.5912044 0.56789137
784 1 0.11643836 0.28380634 0.0000000 0.56070288
785 1 0.48401826 0.40428492 0.5657171 0.45607029
...
880 1 0.43013699 0.00000000 0.4807596 0.36980831
881 1 0.73744292 0.29577073 0.0000000 0.25319489
882 1 0.39977169 0.00000000 0.4867566 0.30990415
883 1 0.25456621 0.00000000 0.8705647 0.26198083
884 1 0.10045662 0.48135782 0.0000000 0.48083067

superplastic coarseagg fineagg age
774 0.00000000 0.651162791 0.37882589 0.016483516
775 0.32298137 0.589534884 0.77722027 0.151098901
776 0.00000000 0.834302326 0.53687908 0.074175824
777 0.00000000 0.941860465 0.04766683 0.491758242
778 0.00000000 0.588662791 0.42247868 0.151098901
779 0.31055901 0.360465116 0.47415956 0.074175824
780 0.40372671 0.441860465 0.47666834 0.074175824
781 0.18012422 0.705232558 0.40215755 0.271978022
782 0.32608696 0.052906977 0.46261917 0.074175824
783 0.18012422 0.705232558 0.40215755 0.035714286
784 0.00000000 0.252906977 0.87581535 0.005494505
785 0.24844720 0.197965116 0.24134471 0.074175824
...
880 0.29192547 0.465697674 0.67987958 0.005494505
881 0.51242236 0.148546512 0.73532363 0.151098901
882 0.36645963 0.502616279 0.70647265 0.035714286
883 0.36335404 0.730523256 0.45534370 0.035714286
884 0.09316770 0.537790698 0.55945810 0.074175824
[ reached getOption("max.print") -- omitted 146 rows ]

• 마지막으로 생성한 신경망을 시각화해보자.

[R Code]

plot(model)

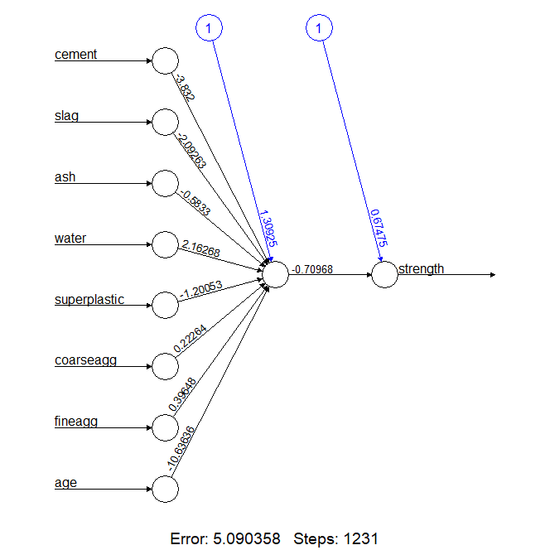
• 시각화를 살펴보면 총 8개의 입력 노드가 있고, 이를 합한 은닉노드 1개, 콘크리트 강도 결과를 예측하는 결과노드 1개로 구성된 것을 알 수 있다.
• 노드와 함께 출력되어있는 수치들은 각 노드에 대한 가중치이며 출력 부분에는 편향 합도 출력되어있다.
• 하단에 명시된 내용은 훈련 단계 수와 오차 제곱 합을 의미하며, 위 모델의 경우에는 총 1231 번의 훈련을 통해 약 5.09에 달하는 오차를 갖고 있다는 것을 알려준다.

3) 모델 성능 평가

• 위의 시각화 및 예측 결과를 통해 어떤 식으로 신경망이 구성되었는지 감을 잡을 수 있지만, 얼마나 적합화됐는지는 확인할 수 없다. 또한 위의 문제는 분류가 아닌 수치예측이므로 confusion matrix를 사용할 수 없다. 따라서 예측한 결과와 실제 값 간의 상관관계를 통해 측정해야한다. ```R [R Code]

cor(pred, test$strength)

```text
[실행결과]

0.8063556

4) 모델 성능 향상

• 앞서 생성해본 모델에 추가적으로 은닉 노드의 수를 5개로 늘려서 학습해보자. ```R [R Code]

model2 <- neuralnet(strength ~ . , data = train, hidden = 5) plot(model2) result2 <- compute(model2, test[,1:8]) pred2 <- result2$net.result cor(pred2, test$strength)

```text
[실행결과]

0.9284925

---

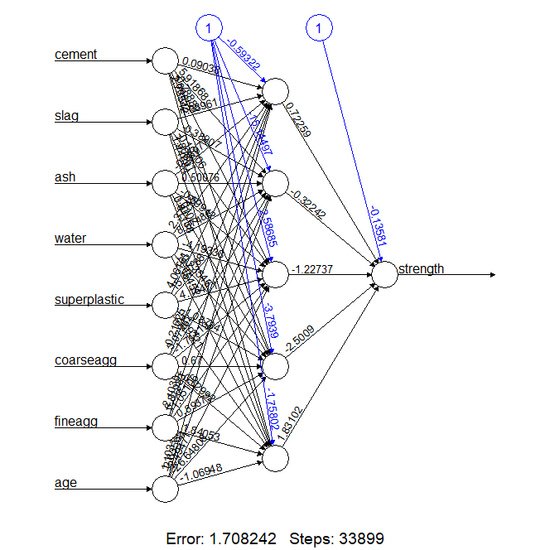
참고자료

https://joohyoung.net/chapter-1-introduction-to-dl/
http://r-bong.blogspot.com/2016/11/neuralnet.html