[R-Machine Learning] 6. 회귀

1. 회귀

• 하나의 종속 변수(반응 변수) 와 독립 변수(설명 변수) 사이의 관계를 명시하는 것
• 독립 값과 의존 값 사이의 관계를 선형으로 가정해 시작한다.
• 일반적으로 결과에 대한 충격을 추정하거나 미래를 추론하는 데이터 간의 복잡한 관계를 모델화하는 데 사용된다.
• 데이터에 대한 추정이 참인지 거짓인지를 나타내는 검증에서도 사용된다.

2. 단순 선형 회귀

• 아래와 같은 형태의 방정식으로 표기되는 직선을 사용해 의존 변수와 하나의 독립 예측 인자 변수 간의 관계를 정의한다.

$ y = ax + b $

1) challenger 호 폭발 사고 원인 분석

• 1986년 1월 28일, 추진 로켓과 연결하는 O형 링이 파손되어 돌발 폭발이 원인이 돼 미국의 스페이스 셔틀인 챌린저호의 승무원 7명이 사망하는 사건이 있었다.
• 이전에 낮은 온도 예측이 발사의 안전성에 영향을 주는지 토론을 하였고 셔틀 구성 부품이 낮은 온도에서 테스트 되지 않았으며 부품들이 영하에서 견딜 수 있는지 확실하지 않았다.
• 데이터 셋은 토론 이전에 성공했던 23회의 셔틀 발사 실험에 기록된 O형 링의 실패 수와 발사 온도에 대한 데이터이다.

2) OLS(Ordinary Least Squares) 회귀

• 최적의 를 결정하기 위한 추정 기법
• 예측한 y 값과 실제 y 값사이에 수직 거리인 오차를 제곱해 구한 총합을 최소가 되게 기울기와 절편을 선택한다.
• 목적 : 실제 y 값과 예측된 y 값 사이의 차이를 e라고 정의할 때, 아래의 방정식을 최소화하는 것

$ \sum {(y_i - \hat{y}_i)}^2 = \sum {e_i}^2 $

• 최소 제곱 오차를 만드는 b의 값은 다음과 같이 계산된다.

$ b = \frac { \sum { (x_i - x)(y_i - y) } }{ \sum { ( {x_i - x} ) }^2 } $

• 공분산
  분자에 대해서는 각 데이터에서 x 평균을 뺀 편차와 각 데이터에서 y 평균의 편차를 제곱근해 구한다.
  위에서 계산한 b 값을 공분산으로 표시하면 다음과 같다.

$ b = \frac {Cov(x, y)}{Var(x, y)} $

• 공분산에 대해서는 다음의 코드를 이용하여 계산이 가능하다.

[R code]

# 데이터 로드
data <- read.csv("dataset/challenger.csv")

# alpha, beta 값 계산
( b <- cov(data$temperature, data$distress_ct) / var(data$temperature) )
( a <- mean(data$distress_ct) - b*mean(data$temperature) )

4) 상관관계

• 직선을 따라 두 변수가 얼마나 가까운지를 나타내는 수치
• 관계는 -1 ~ 1 사이의 값을 갖는다.
• 절대값이 1에 가까울 수록 강한 상관관계를, 0에 가까울수록 약한 상관관계를 갖는다고 해석한다.

• 두 변수간에 상관관계를 측정하기는 독립 변수와 의존 변수 사이에 관계를 판단하는 빠른 방법이다.

• 종류로는 크게 피어슨 상관계수와 스피어만 상관계수가 있다.

• 해당 예제에서는 피어슨 상관계수를 이용하며 수식은 다음과 같다.

• 코드 상으로는 다음과 같이 계산한다.

[R code]

# 상관관계
(r <- cov(data$temperature, data$distress_ct) / (sd(data$temperature) * sd(data$distress_ct)) )

# cor() : 상관관계 함수
cor(data$temperature, data$distress_ct)

[실행결과]

[1] -0.725671

[1] -0.725671

• 위의 예시의 경우 약 -0.73 이므로 온도와 O형 링의 파손 개수 간에 강한 역선형 관계가 있음을 알 수 있다.

3. 다중 선형 회귀

• 단순 선형 회귀의 확장
• 추가적인 독립 변수에 대한 추가 항이 존재한다.

$ y = \alpha + {\beta}_1 x_1 + {\beta}_2 x_2 + … + {\beta}_i x_i + \epsilon $

• 수치 데이터를 모델화하기 위한 가장 일반적인 접근법이다.
• 거의 모든 데이터를 모델화 할 수 있다.
• 속성과 결과 간 관계의 견고성과 크기를 추정할 수 있다.
• 데이터에 대한 강한 가정을 만든다.

• 사전에 모델의 형태가 사용자로부터 명시되어야 한다.

• 위의 식을 선형대수 분야로 가지고 오면 다음과 같이 변경할 수 있다.

$ Y = X \beta + \epsilon $

• 이 때 β 의 최적화추정은 다음과 같이 계산된다.

[R code]

reg <- function(y, x) {
    x <- as.matrix(x)
    x <- cbind(Intercept=1, x)

    solve(t(x) %*% x) %*% t(x) %*% y
}

reg(y = data$distress_ct, x = data[3])

reg(y = data$distress_ct, x = data[3:5])

[실행결과]

[,1]
Intercept 4.30158730
temperature -0.05746032

[,1]
Intercept 3.814247216
temperature -0.055068768
pressure 0.003428843
launch_id -0.016734090

1) 실습 : 선형회귀를 사용한 의료비 예측

• 사용 데이터: 미국의 환자 의료비를 포함한 데이터셋

• 의로 보함에 가입한 1,338명의 수혜자에 대한 정보이다.

• 데이터 셋을 구성하는 컬럼으로는 다음과 같다.
  • age : 보험금 수령인의 나이
  • sex : 약관자의 성별 / 남성(male) 과 여성(female)로 구성
  • bmi : 과체중 혹은 저체중인 사람의 키와 상관관계를 보여주는 신체 용적 지수
  • children : 보험에서 보장하는 아이들 수
  • smoker : 규칙적인 흡연 여부 / Yes, No로 표시
  • region : 미국 내 약관자의 거주지

(1) 데이터 탐색

• 분석할 데이터의 로드 및 구성을 확인한다.

[R code]

setwd("D:/workspace/R")

insurance <- read.csv("dataset/insurance.csv", stringsAsFactors = T)
str(insurance)

# 종속변수(charges)의 분포확인
summary(insurance$charges)

[실행결과]

str(insurance)
'data.frame': 1338 obs. of 7 variables:
$ age : int 19 18 28 33 32 31 46 37 37 60 ...
$ sex : Factor w/ 2 levels "female","male": 1 2 2 2 2 1 1 1 2 1 ...
$ bmi : num 27.9 33.8 33 22.7 28.9 ...
$ children: int 0 1 3 0 0 0 1 3 2 0 ...
$ smoker : Factor w/ 2 levels "no","yes": 2 1 1 1 1 1 1 1 1 1 ...
$ region : Factor w/ 4 levels "northeast","northwest",..: 4 3 3 2 2 3 3 2 1 2 ...
$ charges : num 16885 1726 4449 21984 3867 ...

summary(insurance$charges)
Min. 1st Qu. Median Mean 3rd Qu. Max.
1122 4740 9382 13270 16640 63770

• summary() 결과를 통해서 알 수있듯이, 평균값이 중앙값보다 큰 분포를 보여주기 때문에 오른족 비대칭형태의 분포를 갖는다.
• 좀 더 확실하게 알기 위해 히스토그램을 그려보자.

[R code]

hist(insurance$charges)

[실행결과]

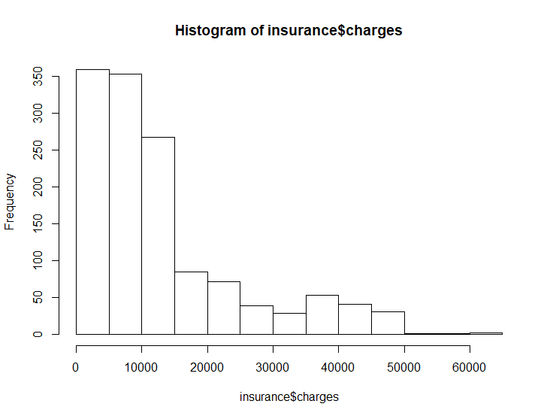
• 위의 시각화를 통해서 개별적으로 대다수는 0 ~ 15000달러 사이의 매년 의료비 지출이 나온다는 것을 알 수 있다.
• 선형 회귀에서는 종속 변수에 대해 정규 분포라고 가정하기 때문에 위의 분포는 이살적이지 않다.
• 추가적으로 회귀 모델은 수치형 데이터로 구성된 데이터를 사용한다.

(2) 속성 간 관계 살피기: 상관관계 매트릭스

• 회귀 모델을 적합화하기전에 독립변수와 종속변수간에 얼마나 관계가 있는지를 확인하는 과정이다.
• 수치형 데이터만 사용가능하기 때문에 age, bmi, children 변수와 charges 변수간의 관계를 확인한다.

[R code]

cor(insurance[,c("age", "bmi", "children", "charges")])

[실행결과]

       age       bmi     children   charges
age 1.0000000 0.1092719 0.04246900 0.29900819
bmi 0.1092719 1.0000000 0.01275890 0.19834097
children 0.0424690 0.0127589 1.00000000 0.06799823
charges 0.2990082 0.1983410 0.06799823 1.00000000

• 위의 결과처럼 각 행의 교차점에서 상관관계는 행과 열로 명시된 변수에 대해 나열된다.
• 대각선 상하의 값은 대칭적이며 같은 변수간의 관계 자체는 항상 완벽한 상관관계를 갖기 때문에 1로 표시한다.

• 실행 결과를 보면, 위의 3가지 독립 변수 중에서 age 변수가 charges 변수가 가장 높은 상관관계를 가진다.

• 위의 내용은 어디까지나 텍스트로 표시된 정보이고, 때문에 한눈에 들어오는 편은 아니다. 따라서 이해도를 높이기 위해 속성간의 관계를 산포도 매트릭스를 통해서 확인해보자

[R code]

pairs(insurance[,c("age", "bmi", "children", "charges")])

[실행결과]

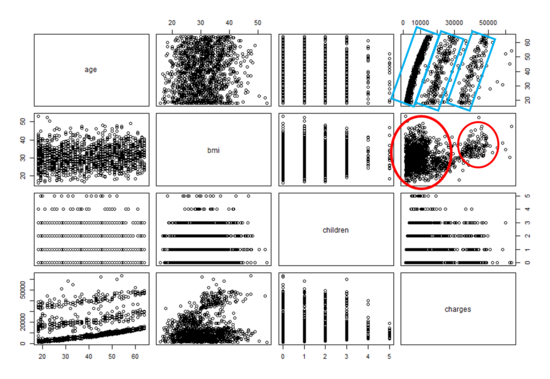
• 상관관계 매트릭스와 마찬가지로 각 행과 열의 교차점은 행과 열의 쌍으로 나타내는 변수의 산포도를 갖는다.

• 위의 결과를 보면, 우선 age와 charges 간의 관계는 일부 상대적인 직선으로 보인다. 반면 bmi 와 charges 간에는 두 개의 다른 그룹을 갖는다는 것을 확인할 수 있다.

• 이번에는 도식에 추가적인 정보를 표시하여 좀더 유용한 시각화로 만들어보자
• 사용할 함수는 psych 패키지의 pairs.panels() 이다.

[R code]

install.packages("psych")
library(psych)

pairs.panels(insurance[,c("age", "bmi", "children", "charges")])

[실행결과]

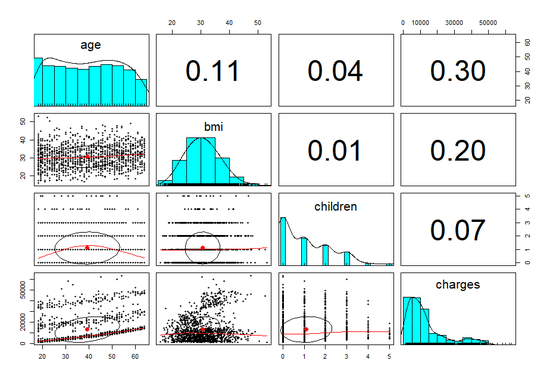
• 구성을 잠깐 보면, 우측 상단은 상관관계 매트릭스와 동일하게 각 변수들 간의 관계를 수치로 표현한 것이다.
• 대각선에는 각 변수 명과 변수에 대한 값의 분포를 보여주는 부분이다.

• 좌측 하단은 산포도에 대한 추가적인 정보들을 같이 표시해준다.

• 위의 결과를 보면, 이전 시각화는 다르게 각 산포도 위에 표시된 상관관계 타원이 보인다.
  • 상관관계 타원은 변수가 얼마나 강하게 관련되었는지 보여주는 시각적 자료
  • 타원의 중앙점은 x 축 변수와 y 축변수에 대한 평균값을 나타냄
  • 모양이 점점 늘어나 타원에 가까울 수록 상관관계가 더 강해짐
• 따라서 위의 자료를 보면 age와 charges 간에는 다른 변수들 간의 관계에 비해 완벽한 타원에 가까운 것을 볼 수 있다.
  반면 bmi 와 charges 간의 관계는 거의 원형에 가깝기 때문에 약한 상관관계를 갖는다고 볼 수 있다.

(3) 데이터 모델 훈련

• 선형 회귀를 적합화하기 위해 stats 패키지의 lm() 함수를 사용한다. 관련 내용은 다음과 같다.

[R Code] 

m <- lm(종속변수 ~ 독립변수, data = 사용데이터)

• 독립변수간의 상호작용은 * 연산자를 이용해 명시할 수 있다.
• 여러 변수를 사용할 경우 + 연산자를 이용해 명시한다.

[R Code]
 
p <- predict(m , 테스트 데이터)

• m 은 lm() 으로 생성된 모델이다.

• 테스트 데이터는 분류기를 만들기 위해 사용되는 훈련데이터와 같은 속성을 가진 테스트 데이터를 포함하는 데이터 프레임이어야 한다.

• 총 의료비와 6개의 독립 변수를 이용해 ins_model 이라는 선형 회귀 모델을 적합화한다.

[R code]

ins_model <- lm(charges ~ age + children + bmi + sex + smoker + region, data = insurance)
# 같은 표현 : ins_model <- lm(charges ~ . , data = insurance)

[실행결과]

Call:
lm(formula = charges ~ age + children + bmi + sex + smoker +
region, data = insurance)

Coefficients:
(Intercept) age children bmi sexmale smokeryes
-11938.5 256.9 475.5 339.2 -131.3 23848.5
regionnorthwest regionsoutheast regionsouthwest
-353.0 -1035.0 -960.1

• 위의 결과를 살펴보자. 우선 Coefficients 부분은 회귀 모델로 추정된 각 변수의 베타 계수를 의미한다. 독립 변수가 0인 경우에는 Intercept(y 절편) 의 계수를 확인한다.
• 모델에서는 6개의 속성을 명시했지만 절편과 더불어 총 8개의 계수를 갖는다. 이유는 lm() 함수가 모델에 포함한 각 팩터 타입에 대해 자동적으로 더미 코딩 기법을 사용했기 때문이다.
• 더미 코딩
  명목형 속성을 각 범주에 대해 이진 변수를 만들어 수치적으로 다루게 한다. 더미 코딩된 변수를 회귀 모델에 추가할 때 하나 범주는 항상 참조 범주로 다루기 위해 남겨준다.
• 때문에 위의 결과를 보면 region의 경우 regionnortheast, regionnorthwest,regionsoutheast, regionsouthwest 로 나뉘지만 regionnortheast 의 경우는 참조 범주로 남겨졌기 때문에 표시되지 않았다.
• 추가적으로 smokeryes, sexmale, regionnorthwest, regionsoutheast, regionsouthwest 의 변수는 음의 상관관계를 갖는다.
• 결론적으로 보험료는 나이가 많을 수록, 비만, 흡연과 같이 부가적인 건강문제와 연관되는 경향을 보인다고 해석된다.

(4) 모델 성능 평가

• ins_model 에서 추정한 매개변수는 독립 변수가 어떻게 종속 변수과 관련되는지를 알려준다. 하지만 데이터에 모델이 얼마나 적합화됬는지는 확인할 수 없다.
• 이를 확인하기 위해 summary() 함수를 사용해 좀 더 자세한 정보를 확인해보자.

[R code]

summary(ins_model)

[실행결과]

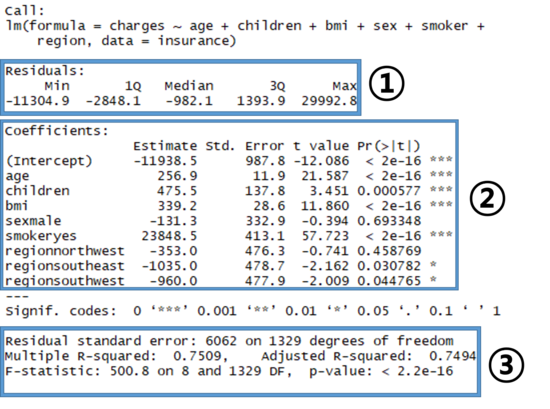
• 위의 결과에서도 명시했듯이, 크게 3부분을 확인하면 된다.

① Residual

• 예측에서 오차에 대한 요약통계를 제공한다.
• 잔차 라고 하며, 실제 값에서 예측한 값을 뺀 결과이다.
• 위의 결과에서는, 오차 범위가 최대 30000까지 차이가 날 수 있다는 것을 의미한다.
• 하지만 50%의 오차가 1Q와 2Q 사이에 존재하기 때문에 예측의 대다수는 실제값이 2,850 달러 이상이고 1,400 달러 이하로 볼 수 있다.

② Coefficients

• 각 변수에 대한 추정 계수를 포함한 여러 측정값들을 표시한 부분이다.

• 눈 여겨볼 부분은 제일 끝에 위치한 Pr(>

  t

  ) 로 각 변수에 대한 t-test 검정의 결과값인 p-value 값이다.

• 통계에서 다뤄질 내용이기에 간단히 이야기하면, 해당 변수가 유용한 변수인지를 확인할 수 있는 부분이라고 보면 되며, 유용한 변수의 기준은 t-test의 유의수준 내에 있는 값을 갖는가 이다.
  일반적으로 유의수준은 5%로 잡으며, 1%, 5%, 10% 로 사용한다.
• 따라서 유의수준을 5%로 할 경우 위의 변수들 중에서는 sexmale, regionnorthwest 변수를 제외하면 나머지 변수들은 전부 유의미한 변수로 볼 수 있다.

③ 모델 해석

• 전반적인 모델에 대해 평가 및 해석이 있는 부분이다.
• 이 중에서 눈 여겨 볼 값은 Multiple R-squared 와 Adjusted R-squared, p-value 부분이다.
  • 먼저 Multiple R-squared 값은 종속 변수의 값에 대해 모델이 얼마나 설명하는지를 측정한 값이다.
  • 상관계수와 유사하게 1에 가까우면 모델은 데이터를 완전하게 설명한다고 해석할 수 있다.
  • 위의 모델은 75%정도 설명할 수 있기에 나쁘지 않다고 보여진다.

• 두번째로 Adjusted R-squared 값은 앞서 본 Multiple R-squared 값에 오차를 적용했을 때의 결과로 위의 예제의 경우 거의 75%에 근사하는 값을 갖기에 나쁘지 않다고 보여진다.

• 마지막으로 p-value 부분은 해당 모델이 가설 검정에 대해 유의미한가를 표시한 부분이라고 볼 수 있다.
• 변수에서와 마찬가지로 유의수준을 5%라고 가정했을 때 위의 결과는 5% 보다 작은 값을 가지므로 유의미한 모델이라고 해석할 수 있다.

2) 모델 성능 향상

• 앞서 언급했듯이, 회귀 모델은 다른 기계학습 접근법과 달리 전형적으로 속성 선택과 모델 명세를 사용자에게 맡긴다.
• 결과적으로 결과에 관련된 속성에 대해 주관적인 지식이 있다면 모델 명세에 알려주기 위해서나 모델의 성능을 잠재적으로 향상하기 위해 이런 정보를 사용한다.

모델 명세: 비선형 관계 추가
* 선형 회귀에서 독립변수와 종속변수 간의 관계는 선형이라고 가정하지만 실제로는 모두 일정하지 않을 수 있기 때문에 사실이 아니다. 따라서 비선형적인 관계를 설명하기 위해 회귀 모델에 고차항을 넣는 방법을 고려할 수 있다.

변환: 수치 변수를 이진 지시자로 변환
* 속성의 결과는 누적되지 않고, 효과는 특정 경계에 도달하는 점을 대충 짐작할 수 있다.
* 속성을 만들기 위해 벡터 안에 각 요소가 특정 조건을 테스트해 조건에 따라 0과 1을 반환하는 ifelse() 함수를 사용한다.

모델 명세: 상호 작용 효과 추가
* 두 속성이 혼합된 효과가 있을 때 상호 작용이라고 한다.
* 두 변수가 상호 작용을 한다면 상호 작용에 대한 내용을 추가해 가정을 테스트 해볼 수 있다.
* 연산자는 *을 사용하고, 확장 형태의 연산은 :을 사용한다.

4. 회귀 트리와 모델 트리의 이해

• 이전에 살펴본 결정트리는 결정노드, 잎 노드에서 플로우 차드와 같은 모델을 만들고, 가지는 예제를 분류하는 데 사용되는 일련의 결정을 정의한다.
• 수치 예측용 트리는 2가지로 구분된다.

① 회귀트리

• 이름과 달리 선형회귀 기법을 사용하지 않고 예제의 평균값을 기반으로 예측한다.

② 모델트리

• 회귀 모델과 유사한 방법으로 자라지만, 다중 선형 회귀 모델은 잎 노드에 도달한 예제로부터 자란다
• 좀 더 정확한 모델을 만들 수 있는 이점이 있지만 회귀 트리보다 이해하기 어렵다.

1) 회귀 트리 장단점

• 장점
  수치 데이터를 모델화할 수 있는 능력을 가진 결정 트리의 장점과 결합한다.
  자동으로 석성을 선택해 대량의 속성에 사용할 수 있다.
  사용자가 발전적인 모델을 명시할 필요가 있다.
  선형회귀보다 훨씬 더 쉽게 일부 데이터에 적합화할 수 있다.
  모델을 해석할 통계적 지식이 필요없다.
  

• 단점
  선형 회귀처럼 일반적으로 사용되지 않는다.
  대량의 훈련 데이터가 필요하다.
  결과에 대한 개별 속성의 전체적인 기준점을 결정하기 어렵다.
  회귀 모델보다 이해하기 쉽다.
  

• 전형적으로 회귀 기법이 수치 예측 문제에 대해 가장 먼저 수행할 수 있지만 일부의 경우에는 수치 결정트리가 좀 더 좋은 결과를 보여주기도 한다.

• 생성과정
  ① 루트 노드로 시작해 데이터를 분할한다.
  ② 결과의 균일성을 가장 증가할 수 있는 속성에 따라 분할과 정복 전략을 사용해 데이터를 나눈다.
  
  • 분류 트리에서 균일성은 엔트로피로서 측정한다.
• 수치 데이터의 경우 균일성은 분산과 표준 편차 또는 평균에서 절대 편차와 같은 통계로 측정될 수 있다.
• 일반적으로 나눔의 기준은 표준 편차 축소(SDR, Standard Deviation Reduction)로 하며, 식은 다음과 같다.

$ SDR = sd(T) - \sum_{i=1}^n {\frac { \vert T \vert }{ \vert T_i \vert } \times sd(T_i) } $

• 아래의 예제를 통해 좀더 자세히 살펴보자.

[R code]

tee <- c(1, 1, 1, 2, 2, 3, 4, 5, 5, 6, 6, 7, 7, 7, 7)
at1 <- c(1, 1, 1, 2, 2, 3, 4, 5, 5)
at2 <- c(6, 6, 7, 7, 7, 7)
bt1 <- c(1, 1, 1, 2, 2, 3, 4)
bt2 <- c(5, 5, 6, 6, 7, 7, 7, 7)

(sdr_a <- sd(tee) - (length(at1) / length(tee) * sd(at1) + length(at2) / length(tee) * sd(at2)))
(sdr_b <- sd(tee) - (length(bt1) / length(tee) * sd(bt1) + length(bt2) / length(tee) * sd(bt2)))

[실행 결과]
[1] 1.202815
[1] 1.392751

• 위의 결과를 보면 표준 편차는 B에 대해 줄어들기 때문에 결정트리는 B를 먼저 사용한다. 따라서 A에 대한 나눔보다 약간 더 균일한 집합을 생성한다.

• 만약 트리가 단 한 번만 나눔을 수행한다고 할 경우 회귀트리는 잘 작동했다고 볼 수 있다. 예제가 T1 이라면 mean(bt1) = 2 로 예측하고, mean(bt2) = 6.25로 예측한다.

• 이에 반해 모델트리는 그룹 bt1의 7개 훈련 예제외 bt2의 8개를 사용해 속성 A대 결과의 선형회귀 모델을 만들 수 있다.

2) 와인 품질 측정하기

• 회귀 트리를 사용해 와인에 등급을 매기는 예제이다.

(1) 데이터 수집

• UCI Machine Learning Data Repository의 데이터 중 하나인 wine quality 데이터를 사용한다.
• 데이터에 대한 추가 정보로는 세계에서 가장 좋은 와인을 생산하는 포른투갈산 vinho Verde 화이트와 레드와인 예제를 포함한다.
• 고급 와인이 기여하는 요소는 레드 와인과 화이트 와인의 다양성이 떼라 다르기 때문에 이번에는 데이터만을 사용한다.
• 데이터는 11가지의 화학적 특성과 총 4,898가지 와인 표본에 대한 정보를 갖는다.
• 등급 결과는 3명의 감정위원이 블라인드 테스트를 통해 0~10사이의 등급으로 구분했다.

(2) 데이터 전처리

• 우선 결과의 분포를 살펴서 모델의 성능 평가를 높이도록 한다.
• 트리모델을 사용하기 때문에 속성의 정규화나 표준화가 필요없다.
• 품질의 분포를 살피기 위해 히스토그램을 그려 확인해보자.

[R code]

setwd("/usr/local/workspace/R")
wine <- read.csv("dataset/whitewines.csv")
str(wine)

hist(wine$quality)

train <- wine[1:3750,]
test <- wine[3751:4898,]

[실행 결과]

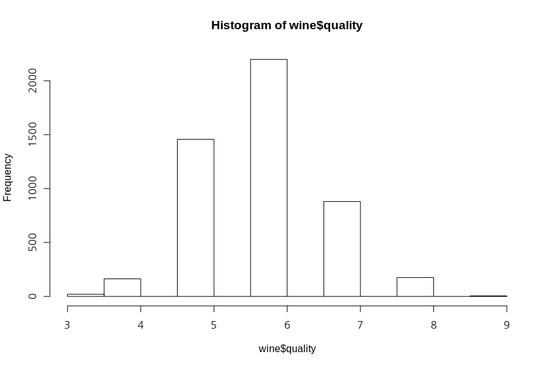
• 위의 시각화를 보게되면 와인 품질 값은 6이 중심이 되는 종모양 분포로 정규 분포를 따른다.
• 만약 이상점이나 다른 잠재적인 데이터 문제에 대해서는 summary(wine) 을 이용해 결과를 확인한다.

(3) 모델 훈련

• 이번에 사용할 모델은 rpart 모델을 이용한다.
• rpart 는 고전적인 CART의 R 구현으로 문서화가 잘 되어있고 가장 신뢰할 수준의 회귀 모델을
• 훈련에 대한 코드는 다음과 같다.

[R code]

install.packages("rpart")
library(rpart)

model <- rpart(quality ~ . , data = train)
model

[실행 결과]

n= 3750 node), split, n, deviance, yval * denotes terminal node 
1) root 3750 2945.53200 5.870933 
2) alcohol< 10.85 2372 1418.86100 5.604975 
4) volatile.acidity>=0.2275 1611 821.30730 5.432030 
8) volatile.acidity>=0.3025 688 278.97670 5.255814 * 
9) volatile.acidity< 0.3025 923 505.04230 5.563380 * 
5) volatile.acidity< 0.2275 761 447.36400 5.971091 * 
3) alcohol>=10.85 1378 1070.08200 6.328737 
6) free.sulfur.dioxide< 10.5 84 95.55952 5.369048 * 
7) free.sulfur.dioxide>=10.5 1294 892.13600 6.391036 
14) alcohol< 11.76667 629 430.11130 6.173291 
28) volatile.acidity>=0.465 11 10.72727 4.545455 * 
29) volatile.acidity< 0.465 618 389.71680 6.202265 * 
15) alcohol>=11.76667 665 403.99400 6.596992 *

• 트리의 각 노드는 결정점에 도달할 예제의 수를 목록화한다.
• 위의 예시로 보면 처음에 총 3,750개의 예제로 시작하고, 그 중 2,372개는 alcohol < 10.85이며, 나머지 1,378개는 alcohol >= 10.85이다. alcohol이 트리의 처음으로 사용됐기 때문에 와인 품질을 예측하는 가장 중요한 속성으로 볼 수 있다.
• 중간에 * 표시로 된 부분은 잎노드를 의미한다.
• 트리 적합화의 좀 더 상세한 요약은 각 노드의 평균 제곱오차와 속성 중요도의 전체적인 측정을 볼 수 있는 summary(model) 를 실행하면 되며 아래와 같은 결과가 도출된다.

[summary(model) 실행 결과]

Call:
  rpart(formula = quality ~ ., data = train) 
  n= 3750 
  CP          nsplit rel error xerror xstd1 
  0.15501053 0 1.0000000 1.0004299 0.024469992 0.05098911 1 0.8449895 0.8459983 0.023353993 0.02796998 2 0.7940004 0.8033877 0.022716774 0.01970128 3 0.7660304 0.7786197 0.021492155 0.01265926 4 0.7463291 0.7613514 0.020762746 0.01007193 5 0.7336698 0.7543939 0.020602407 0.01000000 6 0.7235979 0.7477704 0.02042174
Variable importance 
alcohol 
density 
volatile.acidity 
chlorides 
total.sulfur.dioxide 
free.sulfur.dioxide 34 21 15 11 7 6 residual.sugar sulphates citric.acid 3 1 1 
Node number 1: 3750 observations, complexity param=0.1550105 mean=5.870933, MSE=0.7854751 left son=2 (2372 obs) right son=3 (1378 obs) Primary splits: alcohol < 10.85 to the left, improve=0.15501050, (0 missing) density < 0.992035 to the right, improve=0.10915940, (0 missing) chlorides < 0.0395 to the right, improve=0.07682258, (0 missing) total.sulfur.dioxide < 158.5 to the right, improve=0.04089663, (0 missing) citric.acid < 0.235 to the left, improve=0.03636458, (0 missing) Surrogate splits: density < 0.991995 to the right, agree=0.869, adj=0.644, (0 split) chlorides < 0.0375 to the right, agree=0.757, adj=0.339, (0 split) total.sulfur.dioxide < 103.5 to the right, agree=0.690, adj=0.155, (0 split) residual.sugar < 5.375 to the right, agree=0.667, adj=0.094, (0 split) sulphates < 0.345 to the right, agree=0.647, adj=0.038, (0 split)Node number 2: 2372 observations, complexity param=0.05098911 mean=5.604975, MSE=0.5981709 left son=4 (1611 obs) right son=5 (761 obs) Primary splits: volatile.acidity < 0.2275 to the right, improve=0.10585250, (0 missing) free.sulfur.dioxide < 13.5 to the left, improve=0.03390500, (0 missing) citric.acid < 0.235 to the left, improve=0.03204075, (0 missing) alcohol < 10.11667 to the left, improve=0.03136524, (0 missing) chlorides < 0.0585 to the right, improve=0.01633599, (0 missing) Surrogate splits: pH < 3.485 to the left, agree=0.694, adj=0.047, (0 split) sulphates < 0.755 to the left, agree=0.685, adj=0.020, (0 split) total.sulfur.dioxide < 105.5 to the right, agree=0.683, adj=0.011, (0 split) residual.sugar < 0.75 to the right, agree=0.681, adj=0.007, (0 split) chlorides < 0.0285 to the right, agree=0.680, adj=0.003, (0 split)....
Node number 14: 629 observations, complexity param=0.01007193 mean=6.173291, MSE=0.6838017 left son=28 (11 obs) right son=29 (618 obs) Primary splits: volatile.acidity < 0.465 to the right, improve=0.06897561, (0 missing) total.sulfur.dioxide < 200 to the right, improve=0.04223066, (0 missing) residual.sugar < 0.975 to the left, improve=0.03061714, (0 missing) fixed.acidity < 7.35 to the right, improve=0.02978501, (0 missing) sulphates < 0.575 to the left, improve=0.02165970, (0 missing) Surrogate splits: citric.acid < 0.045 to the left, agree=0.986, adj=0.182, (0 split) total.sulfur.dioxide < 279.25 to the right, agree=0.986, adj=0.182, (0 split)Node number 15: 665 observations mean=6.596992, MSE=0.6075098 Node number 28: 11 observations mean=4.545455, MSE=0.9752066 Node number 29: 618 observations mean=6.202265, MSE=0.6306098

• 위의 결과로 모델에 대한 상세 설명 및 구조, 평가가 가능하지만 좀 더 직관적인 방법을 위해 아래의 시각화 방법을 이용한다.

[R code]

install.packages("rpart.plot")
library(rpart.plot)

rpart.plot(model)

[실행 결과]

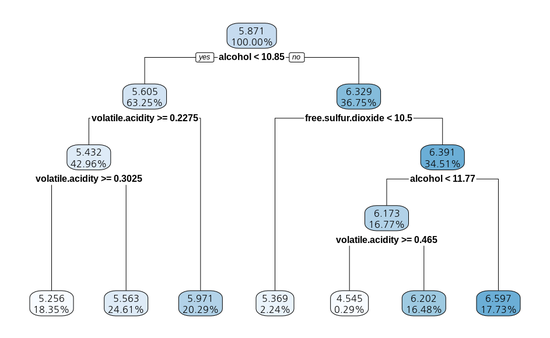
• 앞서 글로 작성된 모델의 구조를 한 눈에 확인할 수 있다는 점에서 유용한 시각화라고 할 수 있다.

(4) 모델 성능 평가

• 테스트 데이터를 적용해 예측하는 회귀 트리 모델을 사용하기 위해 predict() 함수를 사용한다.
• 기본적으로 결과 변수에 대해 추측된 수치 값을 반환해준다.

[R code]

y_pred <- predict(model, test)
summary(y_pred)
summary(wine$quality)

cor(y_pred, test$quality)

[실행 결과]

Min. 1st Qu. Median Mean 3rd Qu. Max. 
4.545 5.563 5.971 5.893 6.202 6.597

Min. 1st Qu. Median Mean 3rd Qu. Max. 
3.000 5.000 6.000 5.878 6.000 9.000

[1] 0.5369525

(5) 평균 절대 오차(MAE, Mean Absolute Error)를 이용한 성능 측정

• 평균적으로 예측 값과 실제 값이 얼마나 차이가 나는지 고려하는 방법이다.
• 계산 식은 아래와 같다.

$ MAE = \frac {1}{n} \sum_{i=1}^n { \vert e_i \vert } $

• 위의 식에서 n은 예측 갯수, e 는 예측 i 에 대한 오차를 나타낸다.
• 본질적으로 오차에 대한 절대값의 평균이며, 예측 값과 실제 값 사이에 차이가 있다.
• 앞서 본 예측에 대한 평균절대오차는 다음과 같다.

[R code]

MAE <- function(actual, predicted) {
  mean(abs(actual - predicted))
}

MAE(y_pred, test$quality)

mean(train$quality)

[실행 결과]

[1] 0.5872652
[1] 5.870933

• 결과를 통해서 알 수 있듯, 모델의 예측과 실제 품질 점수의 차이는 약 0.59임을 나타내며 품질의 범위는 0 ~ 10이기 때문에 모델이 잘 작동함을 알려준다.
• 회귀 트리는 imputed mean 결과보다 평균적으로 실제 품질등급에 가깝지만 값이 큰 편은 아니다. 동일 데이터로 코르테즈 신경망으로 분석한 결과는 0.58이고 서포트 벡터 머신의 경우 0.45 MAE로 보고 되었다.