[Python Machine Learning] 9. SOM

1. SOM(자가 조직 지도, Self-Orginizing Map) 대뇌피질 중 시각피질의 학습 과정을 모델화한 인공신경망으로 차원이 축소화된 데이터셋을 토폴로지 개념으로 효과적인 표현을 만들 수 있는 기법이다. 일반적인 신경망과 달리, 비지도학습 기법 중 하나로 주로 군집화에서 많이 사용된다. 또한 데이터의 규모가 작은 경우에는 kMeans 클러스터링과 유사하게 동작하지만, 데이터의 규모가 커질수록 복잡한 데이터셋의 토폴로지를 잘 나타내는 성향이 있다.
   

1) SOM 구조

노드의 그리드로 구성되며, 각 노드에는 입력 데이터셋과 동일한 차원의 가중치 벡터가 포함되어있다. 각 노드에는 입력 데이터셋과 동일한 차원의 가중치 벡터가 포함되어 있으며, 무작위로 초기화 될 수 있지만 대략적인 근사치를 기반으로 초기화할 경우 학습속도가 빠를 수 있다.

2) SOM 알고리즘 진행절차

모든 가중치 벡터의 데이터 공간 상에서 유클리디언 거리를 계산해 가장 좋은 노드인 BMU (Best Machine Unit)을 찾는다. 입력 벡터 쪽으로 일부 조정이 된다. 이웃 노드도 일부 조정을 하며, 이웃 노드의 이동 정도는 네이버후드 함수에 의해 결정된다. 네트워크가 수렴할 때까지 샘플링을 사용해 여러 차례 반복적으로 이뤄진다.

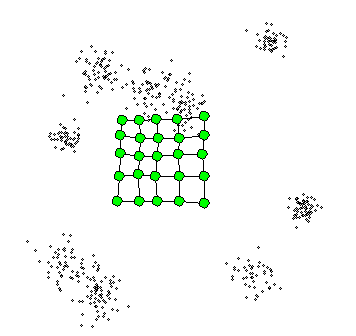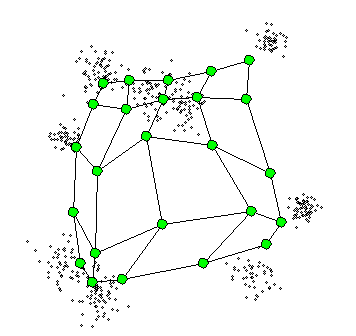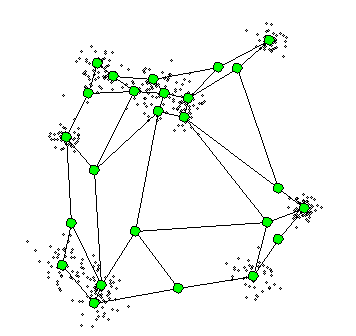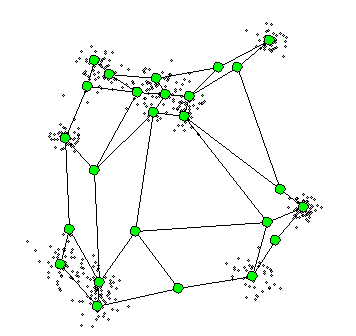
위의 연두색 부분이 격자 벡터이며 그림에서 볼 수 있듯이, 랜덤으로 초기화되고 격자벡터의 업데이트 폭은 항상 일정하지 않다. 아래의 코드는 손글씨 이미지 데이터를 SOM으로 구분한 것이다. SOM 패키지는 아래의 파일을 import 해서 사용하면 된다.

[Python Code]

import numpy as np

from sklearn.datasets import load_digits
from som import Som
from pylab import plot, axis, show, pcolor, colorbar, bone

digits = load_digits()
data = digits.data
labels = digits.target

# SOM 모델링
som = Som(16, 16, 64, sigma=1.0, learning_rate=0.5)
som.random_weights_init(data)

print("Initiating SOM")

som.train_random(data, 10000)
print("\nSOM Processing Complete")

bone()
pcolor(som.distance_map().T)
colorbar()

[실행결과]

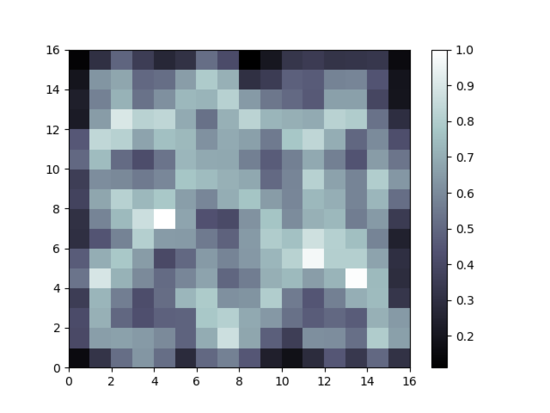
코드를 잠깐 분석해보면, 먼저 매필 관련 차원과 입력 데이터에 대한 차원을 입력인자로 설정한다. 이 때 sigma 의 경우 가우시안 네이버후드 함수의 분포정도를 의미한다. 값이 너무 작게되면 눈금의 중심근처로 집중될 수 있다는 점에 유의해서 설정한다. 반대로 값이 너무 크면 그리드가 일반적으로 중심을 향해 커다란 빈 공간을 생성하는 결과를 만들 수 있다. learning_rate 는 SOM의 초기 학습 속도를 스스로 컨트롤할 수 있는 값이라고 정의할 수 있다. 식은 다음과 같다.

$ LearningRate(t) = LearningRate / (1+ (t/0.5t)) $

위에서 t는 반복횟수 인덱스를 의미한다. 이번에는 가중치를 무작위로 부여해 SOM 알고리즘을 초기화한다. 이 후 각 클래스에 대해 레이블과 색상을 지정해 SOM 알고리즘을 통해 생성된 클래스를 화면상에 표출할 때 쉽게 구분할 수 있다.

[Python Code]

labels[labels == '0'] = 0
labels[labels == '1'] = 1
labels[labels == '2'] = 2
labels[labels == '3'] = 3
labels[labels == '4'] = 4
labels[labels == '5'] = 5
labels[labels == '6'] = 6
labels[labels == '7'] = 7
labels[labels == '8'] = 8
labels[labels == '9'] = 9

marker = ['o', 'v', '1', '3', '8', 's', 'p', 'x', 'D', '*']
colors = ["r", "g", "b", "y", "c", (0,0.1,0.8), (1, 0.5, 0), (1,1,0.3), "m", (0.4, 0.6, 0)]
for cnt, xx in enumerate(data):
    w = som.winner(xx)

plot(w[0]+.5, w[1]+.5, marker[labels[cnt]], markerfacecolor="None", markeredgecolor=colors[labels[cnt]], markersize=12, markeredgewidth=2)
axis([0, som.weights.shape[0], 0, som.weights.shape[1]])
show()

[실행결과]

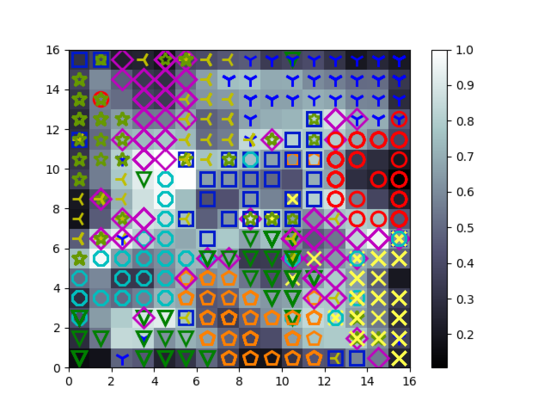
16 x 16 노드의 SOM 시각화 결과를 보여주며 위의 그림과 같이 각 클러스터를 토폴로지 상에 구분 가능하도록 표시해두었다. 일부 클래스는 SOM의 공간 여러곳에 걸쳐있는 경우도 있지만, 대다수의 클래스는 서로 다른 영역에 위치가 있다는 것을 보아, SOM 알고리즘이 상당히 효과적이라는 것을 알 수 있다.

[참고자료]
https://ratsgo.github.io/machine%20learning/2017/05/01/SOM/