[Python Machine Learning] 8. 인공신경망

1. 인공 신경망

1) 개요 및 역사

사람의 뇌가 어떻게 복잡한 문제를 푸는지에 대한 가설과 모델을 기반으로 만들어진 알고리즘이다. 초기 연구는 워렌 멕컬록과 월터 피츠가 처음 뉴런의 작동 방식을 기술하면서 시작되었다. 멕컬록-피츠 뉴런 모델인 로젠브라트의 퍼셈트론이 1950년대 처음 구현된 이후 수십년간 많은 머신러닝 기술자들은 신경망에 대한 연구에 대한 관심을 조금씩 접기 시작했다. 이유는 다층 신경망을 훈련시킬 적절한 방법이 없었기 때문이다. 하지만 1986년 제프리 힌튼 , 루멜하트, 윌리엄스 세 명이 신경망을 효과적으로 훈련시킬 수 있는 역전파 알고리즘을 재발견하게 되고 난 후 신경망에 대한 관심이 다시 높아지기 시작했다.

2. 인공뉴런 : 퍼셉트론

1) 퍼셉트론

앞서 설명한 것처럼 멕컬록과 피츠는 신경 세포를 이진 출력을 내는 간단한 논리 회로로 표현했다. 입력 신호가 들어오면 각 입력으로부터 받아들이는 가중치를 곱한 후 합한 값을 출력으로 내는 데 이 때 해당 출력 값이 특정 임계 값을 넘을 경우 신호가 생성되고 출력을 전달하는 식으로 표현했다.
위의 내용을 수학적으로 해보면, 입력 값을 x 라고 정의하고, 가중치를 w 라고 가정하자. 두 변수는 모두 벡터 형태이며, 이 때 신경망의 출력 값을 수식으로 표시하면 다음과 같이 표현할 수 있다.

$ z = w_1x_1 + w_2x_2 + … + w_nx_n $

출력 값이 계산됬다면, 해당 출력에 대해 특정 임계 값을 넘는지를 확인해야한다. 이 함수를 Φ(x) 라고 할 때, 출력 값 결정 함수의 표현은 다음과 같다.

$ \Phi (z) = \begin{cases} 1 & z \ge \theta \text{ 일 때} \ -1 & \text { 그 외} \end{cases} $

출력 값 결정함수는 다른 말로 활성 함수 라고 하며, 퍼셉트론에서의 활성함수는 단위 계단 함수를 변형한 함수이다. 다음으로 퍼셉트론의 학습 규칙에 대해서 알아보자. 전반적인 아이디어는 뇌의 누런 하나가 작동하는 방식을 흉내내려는 환원주의 접근 방식을 사용했다. 즉, 출력을 내거나, 내지않거나 라는 2가지의 경우만 존재한다. 요약을 하면 다음과 같다.

① 가중치를 0 또는 랜덤한 작은 값으로 초기화한다.
② 각 훈련 샘플에서 출력 값을 계산하고 가중치를 업데이트 한다.

2) 역전파 알고리즘

역전파 알고리즘의 핵심은 신경망의 가중치 값을 이전 결과의 오차를 반영하여 업데이트 해주는 것에 있다. 가중치의 업데이트는 동시에 진행되며, 이를 수학적으로 표현하면 다음과 같다.

$ w_j \ := w_j + \Delta w_j $

위의 식에서 Δwj 는 wj 를 업데이트 하는 데 사용되는 값을 의미한다. 이 때 Δwj 를 풀어보면 다음과 같다.

$ \Delta w_j = \eta (y^{(i)} - { \hat {y} }^{(i)}) x_j^{(i)}$

여기서 η 는 학습률을 의미하며 일반적으로 0 ~ 1 사이의 값을 가진다. 결과적으로 위 식은 실제 값과 예측 값 사이의 오차에 학습률 만큼을 곱해줌으로서 새로운 가중치를 구해 전체적으로 업데이트 해주는 과정이라고 할 수 있다. 만약 퍼셉트론이 정확하게 예측한다면 가중치의 변경 없이 유지가 되지만, 잘못 예측하는 경우에는 가중치를 양성 또는 음성 클래스 방향으로 이동시킨다.

3) 퍼셉트론 API 구현

마지막으로 지금까지 내용을 이용해 퍼셉트론 API 를 구현해보자. 코드는 다음과 같다.

[Python Code]

import numpy as np

class perceptron:
    def __init__(self, eta=0.01, n_iter=50, random_state=1):
        self.eta = eta
        self.n_iter = n_iter
        self.random_state = random_state

    def fit(self, x, y):
        rgen = np.random.RandomState(self.random_state)
        self.w = rgen.normal(loc=0.0, scale=0.01, size=1 + x.shape[1])

        self.errors = []

        for _ in range(self.n_iter):
            errors = 0
            for xi, target in zip(x, y):
                update = self.eta * (target - self.predict(xi))
                self.w[1:] += update * xi
                self.w[0] += update
                errors += int(update != 0.0)

            self.errors.append(errors)

        return self

    def net_input(self, x):
        return np.dot(x, self.w[1:]) + self.w[0]

    def predict(self, x):
        return np.where(self.net_input(x) >= 0.0, 1, -1)

위의 API 를 이용해 붓꽃 데이터 분류를 테스트 해보자.

[Python Code]

import pandas as pd
import numpy as np

import matplotlib.pyplot as plt

iris = pd.read_csv("https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data", header=None)
iris.tail

y = iris.iloc[0:100, 4].values
y = np.where(y == 'Iris-setosa', -1, 1)

x = iris.iloc[0:100, [0, 2]].values

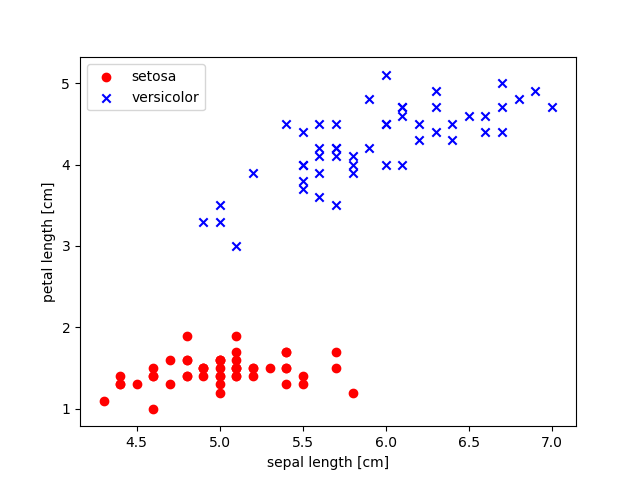
plt.scatter(x[:50, 0], x[:50, 1], color='red', marker='o', label = 'setosa')
plt.scatter(x[50:100, 0], x[50:100, 1], color='blue', marker='x', label = 'versicolor')
plt.xlabel('sepal length [cm]')
plt.ylabel('petal length [cm]')
plt.legend(loc='upper left')
plt.show()

ppn = perceptron(eta=0.1, n_iter=10)
ppn.fit(x, y)

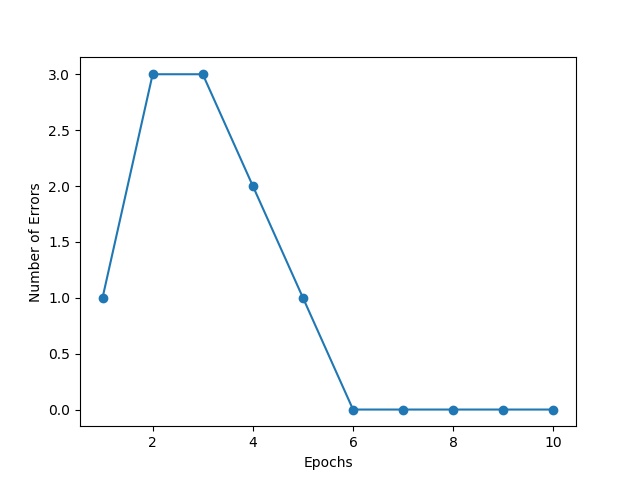
plt.plot(range(1, len(ppn.errors) + 1),
ppn.errors, marker='o')
plt.xlabel('Epochs')
plt.ylabel('Number of Errors')
plt.show()

[실행 결과]

3. 단일층 신경망

1) 아달린 알고리즘

다층 신경망을 설명하기에 앞서 단일층 신경망의 구조를 먼저 이해해야한다. 단일층 신경망의 대표적인 예시로는 아달린 알고리즘이 있으며, 구조는 아래 그림과 같다.

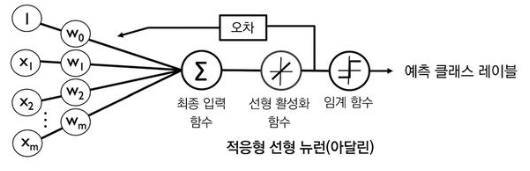
아달린은 적응형 선형 뉴런이라고 하며 버나드 위드로우와 테드 호프가 개발한 신경 뉴런 모델이다. 앞서 본 퍼셉트론과 달리, 아달린은 활성함수를 연속 함수를 사용하며, 수식으로 표현하면 다음과 같다.

$ \Phi (w^Tx) = w^Tx $

이는 진짜 클래스 레이블과 선형 활성 함수의 실수 출력값을 비교해 모델의 오차를 계산하고 가중치를 업데이트 하기 때문에, 레이블 간의 오차를 계산하는 퍼셉트론 보다 가중치 업데이트의 성능이 향상되었다고 볼 수 있다.

2) 경사 하강법

아달린 알고리즘의 또다른 큰 특징인 계산된 출력값과 실제 클래스 사이의 제곱 오파합으로 가중치를 학습할 비용함수를 정의한다는 점이다. 식은 다음과 같다.

$ J(w) = \frac {1} {2} \sum _i {(y^{(i)} - \Phi (z^{(i)}))}^2 $

위 식을 자세하게 살펴보면, Φ(z(i)) 가 예측한 결과인 y^ 을 의미하며, 식의 앞부분에 1/2 을 곱해준 이유는 이후에 진행될 미분에서 식을 좀 더 간소화시키기 위한 장치라고 보면 된다. 미분이 가능한 이유는 앞서 언급한 연속함수(정확히는 선형활성화함수)를 사용하기 때문에 비용함수가 미분가능해지기 때문이다.
경사하강법이란 지도학습 알고리즘의 핵심 구성 요소를 학습하는 동안 최적화하기 위한 기법 중 하나로, 전체 출력되는 값에 대해 가중치 업데이트의 비용을 최소화 시키는 값을 찾는 것이 목적이다. 때문에 비용함수의 미분한 결과와 반대되는 방향으로 조금씩 이동하여 가중치를 업데이트 시키게 되고, 최소값에 도달하면 정지하게 되는다.

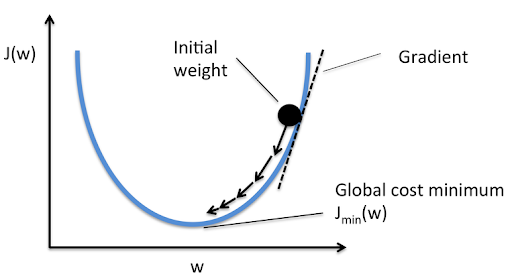
이동 크기는 경사의 기울기와 학습률로 결정된다. 위의 수식으로 비용함수의 그레디언트를 계산하는 과정은 다음과 같다. 먼저, 가중치 업데이트의 수식을 살펴보자.

$ w := w + \Delta w $

이 때, 학습률이 η 이고, 가중치 변화량인 Δw 는 음수의 그레디언트에 학습률을 곱한 것이라고 정의하면, Δw 를 다음과 같이 표현할 수 있다.

$ \Delta w = - \eta \nabla J(w) $

비용함수의 그레디언트를 계산하려면, 각 가중치 $ w_j $ 로 미분을 해줘야하며, 계산 결과는 다음과 같다.

$ \frac {\delta J} {\delta w_j} = - \sum _i (y^{(i)} - \Phi (z^{(i)})) x_j^{(i)} $

앞서 Δw 를 -η▽J(w) 라고 했으며, -▽J(w) 가 음수인 그레디언트라고 했었다. 그레디언트는 비용함수인 J(w)를 각 가중치 wj 로 미분한 결과이기 때문에, 위의 두 개 식으로 정리하면, 업데이트 되는 가중치 $w_j$ 에 대한 식을 표현할 수 있게 된다.

$ \Delta w_j = - \eta \frac {\delta J} {\delta w_j} = \eta \sum _i (y^{(i)} - \Phi (z^{(i)})) x_j^{(i)} $

3) 아달린 알고리즘 구현

위의 내용을 기반으로 아달린 알고리즘 API 를 구현해보자. 코드는 다음과 같다.

[Python Code]

import numpy as np

class AdalineGD(object):
    def __init__(self, eta=0.01, n_iter=50, random_state=1):
        self.eta = eta
        self.n_iter = n_iter
        self.random_state = random_state

    def fit(self, x, y):
        rgen = np.random.RandomState(self.random_state)
        self.w = rgen.normal(loc=0.0, scale=0.01, size=1 + x.shape[1])
        self.costs = []

        for i in range(self.n_iter):
            net_input = self.net_input(x)
            output = self.activate(net_input)
            errors = y - output
            self.w[1:] += self.eta * x.T.dot(errors)
            self.w[0] += self.eta * errors.sum()
            cost = (errors**2).sum() / 2.0
            self.costs.append(cost)

        return self

    def net_input(self, x):
        return np.dot(x, self.w[1:]) + self.w[0]

    def activate(self, x):
        return x

    def predict(self, x):
        return np.where(self.activate(self.net_input(x)) >= 0.0, 1, -1)

퍼셉트론 API 와 비교했을 때, 전체 훈련 데이터셋을기반으로 그래디언트를 계산하는 것을 알 수 있고, 절편은 self.eta * errors.sum() 한 결과를, 가중치 1 ~ m 번째 까지는 self.eta * x.T.dot(errors) 로 계산한 결과로 표현했다. 코드에서 activate() 메소드는 항등함수를 표현하기 위한 것이며, 결과에는 영향을 미치지 않는다.
앞서 경사하강법 이용 시, 비용은 학습률과 기울기에 영향을 받는다고 언급했었다. 이를 위해 서로 다른 학습률로 설정했을 때 얼마나 차이가 나는지를 확인해보도록 하자. 코드는 다음과 같다.

[Python Code]

import pandas as pd
import matplotlib.pyplot as plt

iris = pd.read_csv("https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data", header=None)
iris.tail

x = iris.iloc[0:100, [0, 2]].values

y = iris.iloc[0:100, 4].values
y = np.where(y == 'Iris-setosa', -1, 1)

fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(10, 4))

ada1 = AdalineGD(n_iter=10, eta=0.01).fit(x, y)
ada2 = AdalineGD(n_iter=10, eta=0.0001).fit(x, y)

ax[0].plot(range(1, len(ada1.costs) + 1), np.log10(ada1.costs), marker='o')
ax[0].set_xlabel('Epochs')
ax[0].set_ylabel('log(Sum-Squared Error)')
ax[0].set_title('Adaline - Learning_rate = 0.01')

ax[1].plot(range(1, len(ada2.costs) + 1), np.log10(ada2.costs), marker='o')
ax[1].set_xlabel('Epochs')
ax[1].set_ylabel('Sum-Squared Error')
ax[1].set_title('Adaline - Learning_rate = 0.0001')

[실행 결과]

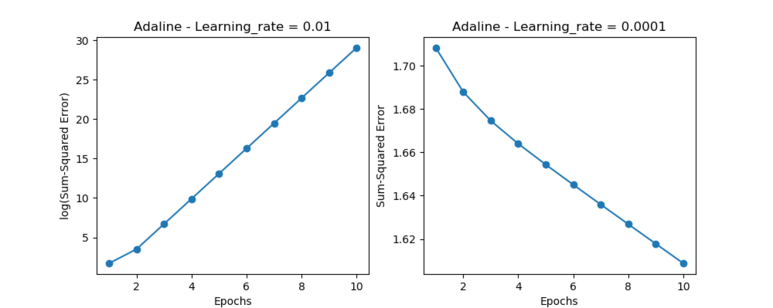
결론부터 말하자면, 위의 2개 그래프 모두 문제가 있다. 왼쪽 그래프의 경우에는 학습률을 너무 높게 잡아서 비용함수가 최소화되지 못하고 오차는 점점 증가하는 추세를 보여준다. 반면 오른쪽 그래프의 경우에는 학습률이 너무 작아서 그레디언트의 이동을 아주 미세하게 진행하고 있다. 전역 최소값에 도달하려면 더 많은 에포크가 필요로 하며, 자원상 낭비로 이어질 수 있다.

4) 특성 스케일 조정 : 표준화(Standardization)

앞서 본 것처럼, 학습률이 너무 크면 발산해버리고 너무 작으면 학습의 진행이 더디거나, 설명하진 않았지만, 지역 최소값에 고립되는 Local Minima 문제에 빠질 수 있다. 때문에 어떤 식으로든 특성 스케일을 해줘야 하며, 경사하강법의 경우 특성 스케일을 조정하여 혜택을 볼 수 있는 알고리즘 중 하나이다. 이번 예제에서는 스케일 조정 기법 중 하나인 표준화를 살펴볼 것이다. 표준화란 각 특성의 평균을 0에 맞추고 표준편차를 1로 만들어 모든 샘플이 정규분포를 따르도록 스케일링 해주는 기법이다. 예를 들어 j 번째의 특성을 표준화하려면, 샘플 값에서 평균인 μj 를 뺀 후 표준편차 σj 로 나누면 된다.

$ {x”}_j = \frac {x_j - {\mu }_j} {\sigma _j} $

표준화가 경사하강법에 도움이 되는 이유는 더 적은 단계를 거쳐 최적 값을 찾기 때문이다. 아래 그림은 분류문제에서 모델의 가중치에 따른 비용함수의 등고선을 표시한 것으로, 왼쪽이 표준화 전이고 오른쪽이 표준화 한 후의 비용함수 등고선이다.

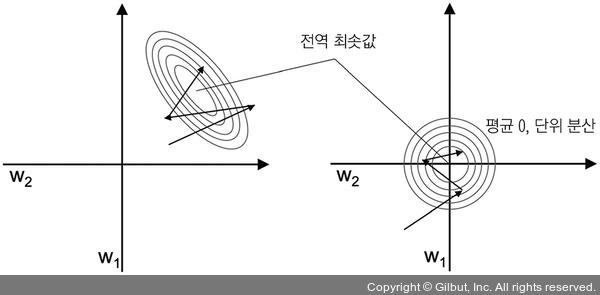
그림에서의 화살표는 경사하강법으로 가중치가 업데이트 되는 방향을 의미하고 화살표의 길이가 업데이트의 비용을 의미하는데, 왼쪽 그래프 보다 오른쪽 그래프가 좀 더 안정된 이동을 보여준다고 해석된다. 이는 오른쪽 그래프처럼 최적화를 하게 되면, 표준화를 하지 않았을 때 보다 더 빠르게 최적 값을 찾는다고 해석할 수 있다. 위의 내용을 바탕으로 표준화하는 코드와 그에 대한 결과를 출력하는 코드를 작성해보자.

[Python Code]

# 표준화
x_std = np.copy(x)
x_std[:,0] = (x[:,0] - x[:,0].mean()) / x[:,0].std()
x_std[:,1] = (x[:,1] - x[:,1].mean()) / x[:,1].std()

ada_standard = AdalineGD(n_iter=15, eta=0.01)
ada_standard.fit(x_std, y)

plt.scatter(x_std[:50, 0], x_std[:50, 1], color='red', marker='o', label = 'setosa')
plt.scatter(x_std[50:100, 0], x_std[50:100, 1], color='blue', marker='x', label = 'versicolor')
plt.xlabel('sepal length [cm]')
plt.ylabel('petal length [cm]')
plt.legend(loc='upper left')
plt.show()

plt.plot(range(1, len(ada_standard.costs) + 1), ada_standard.costs, marker='o')
plt.xlabel('Epochs')
plt.ylabel('Sum-Squared Error')
plt.show()

[실행 결과]

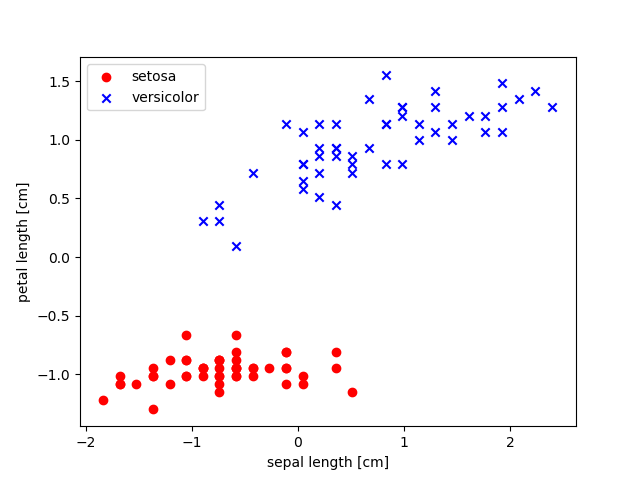
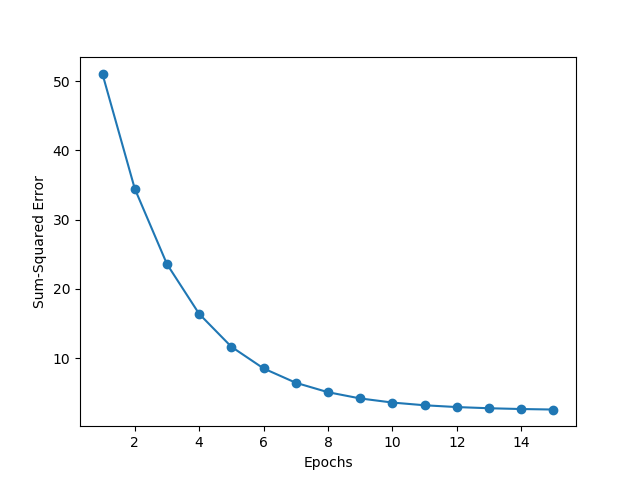
앞서 학습률이 0.01 이였던 그래프와 비교했을 때, 표준화를 적용한 결과가 수렴하는 형태를 보여준다는 것을 알 수 있다.

4. 다층 신경망 구조

1) MLP (Multi Layer Perceptron)

이번에는 신경망이 여러 층으로 구성된 다층 신경망에 대해서 살펴보자. 그 중에서 신경망을 구성하는 모든 노드가 전부 연결되어있는, 완전 연결 네트워크인 다층 퍼셉트론(MLP, Multi Layer Perceptron) 이다. 다층 퍼셉트론을 비롯해 여러 층을 갖고 있는 신경망의 경우 아래 그림과 같이 크게 3부분으로 나눌 수 있다.

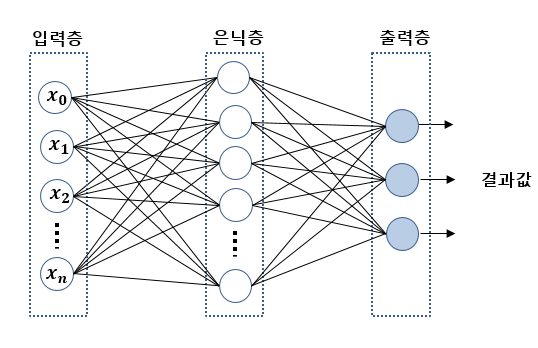
입력층은 말그대로 입력 값을 받는 층으로 입력 갯수만큼 노드가 생성된다. 은닉층은 입력층으로부터 넘어온 데이터를 처리하는 계층으로 위의 그림상에서는 1개 층이지만, 2개 이상의 층으로 구성되는 경우에는 심층 신경망 이라고 부른다. 마지막으로 출력층은 은닉층에서 처리된 결과를 받아 최종 결과값을 계산해주는 역할을 수행한다. 주로 결과 클래스의 개수에 따라 노드 수가 결정된다.
신경망의 학습은 크게 2단계로 나눠지며, 출력을 계산하는 정방향 전파(Feed-Forward Propagation)와 출력된 결과를 통해 각 노드의 가중치를 재설정하는 역전파(Back-Propagation) 과정으로 나뉜다.

2) 신경망의 학습법

MLP 모델을 포함한 여러 인공신경망은 아래와 같이 3단계로 학습을 진행한다.

① 입력층에서 시작해 정방향으로 훈련데이터의 패턴을 네트워크에 전파해 출력을 생성한다.
② 생성된 출력을 기반으로 역전파에서 다룰 비용함수를 이용해 최소화할 오차를 계산한다.
③ 네트워크에 있는 모든 가중치에 대한 도함수를 찾아 오차를 역전파 하고 모델을 업데이트 한다.

(1) 정방향 전파(Feed-Forward Propagation)

신경망에 입력 값이 들어오면 가장 먼저 수행되는 작업이며, 입력에 대한 출력을 계산하게 된다. 설명에 앞서 입력 벡터를 구성하는 각각의 입력을 x, 입력에 대한 가중치 벡터의 각 가중치를 w라고 가정하고, 은닉층의 결과인 활성화 출력값을 z, 활성화함수는 Φ(x) 라고 표현하자. 앞서 본 것 처럼 신경망을 구성하는 모든 노드는 이어져 있기 때문에 하나의 은닉층에서 나오는 활성화 출력값은 다음과 같이 표현할 수 있다. 예시로 첫번째 은닉층에 대한 활성화 출력값을 살펴보자.

$ z_1 = w_{0,1} x_0 + w_{1,1} x_1 + w_{2,1} x_2 + … + w_{n,1} x_n $

가중치의 0,1 은 입력 0에서 은닉층 1번 노드까지의 가중치를 의미하며, 위의 그림에서는 화살표에 해당한다. 활성화 출력값을 a라고 표현할 때, a가 만들어지는 과정은 은닉층 1번으로 향하는 모든 입력벡터에 대해 가중치 벡터를 내적하고, 결과값을 활성화 함수의 입력으로 넣어주면 된다.
단, 활성화함수는 그래디언트 기반 방식을 사용하여 뉴런과 연결된 가중치를 학습해야되기 때문에 반드시 미분가능한 함수를 사용해야되며, 위의 경우 시그모이드 함수를 사용했다.( Φ(x) 는 시그모이드 함수를 의미한다. )
시그모이드 함수란 앞서 본 로지스틱 함수인데, 원점을 지나는 S자 모양의 함수이며, 0~1사이의 로지스틱 분포로 매핑한다. 신경망에서는 사용되는 이유는 이미지 분류와 같은 복잡한 문제를 해결하기 위해 미분이 가능한 비선형 함수를 사용하게 되며, 그 중 가장 먼저 사용된 것이 시그모이드 함수이다.
특히 지금 살펴보고 있는 MLP가 대표적인 피드포워드형 신경망인데, 피드포워드라는 표현을 사용한 이유는 입력을 각 층에서 순환시키는 것이 아닌 다음 층으로 그대로 전달하는 특징을 갖고 있기 때문이다.

결과적으로 보자면, 활성화 출력 값의 결과는 시그모이드 함수를 사용한 결과이기 때문에 0 ~ 1 사이의 연속적인 값을 반환하는 로지스틱 회귀 유닛이라고도 할 수 있다. 위의 내용을 구현하기 위해 이미지 분류의 “Hello World” 라고 할 수 있는 MNIST 데이터를 이용하여, 코드로 구현해보자.

[Python Code]

import os
import struct
import numpy as np
import pandas as pd

import matplotlib.pyplot as plt

def load_mnist(path, kind="train"):
    label_path = os.path.join(path, '%s-labels-idx1-ubyte' %kind)
    image_path = os.path.join(path, '%s-images-idx3-ubyte' %kind)

    with open(label_path, 'rb') as lbpath:
        magic, n = struct.unpack('>II', lbpath.read(8))
        # > : 빅 엔디언을 의미
        # I : 부호가 없는 정수를 의미

        labels = np.fromfile(lbpath, dtype=np.uint8)

    with open(image_path, 'rb') as imgpath:
        magic, num, rows, cols = struct.unpack('>IIII', imgpath.read(16))
        images = np.fromfile(imgpath, dtype=np.uint8).reshape(len(labels), 784)
        images = ((images / 255.) - .5) * 2

    return images, labels

x_train, y_train = load_mnist('dataset/MNIST/raw', kind='train')
x_test, y_test = load_mnist('dataset/MNIST/raw', kind='t10k')

print("행 : %d, 열 : %d\n" % (x_train.shape[0], x_train.shape[1]))
print("행 : %d, 열 : %d\n" % (x_test.shape[0], x_test.shape[1]))

fig, ax = plt.subplots(nrows=2, ncols=5, sharex=True, sharey=True)
ax = ax.flatten()

for i in range(10):
    img = x_train[y_train == i][0].reshape(28, 28)
    ax[i].imshow(img, cmap='Greys')
    
ax[0].set_xticks([])
ax[1].set_yticks([])

plt.tight_layout()
plt.show()

[실행 결과]

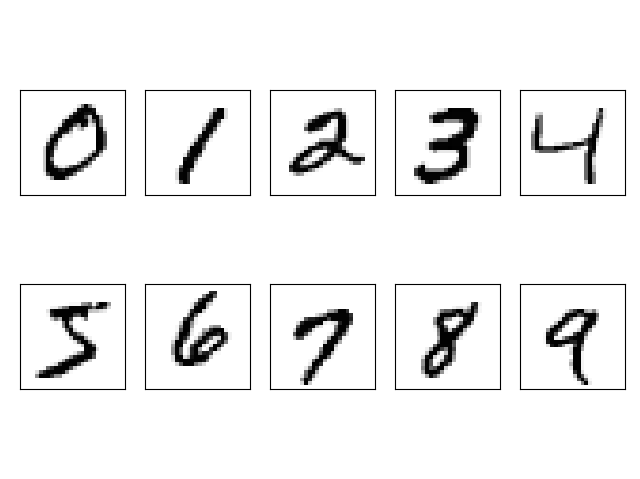
위의 코드에서 특이한 사항이 몇가지 있다. 우선 MNIST 데이터 로드 하는 과정에서 다음의 코드를 볼 수 있다.

[Python Code]

...

with open(label_path, 'rb') as lbpath:
    magic, n = struct.unpack('>II', lbpath.read(8))

...

주석으로도 명시해두었지만, 좀 더 자세하게 설명하고자 다시 언급했다. MNIST 데이터셋에 대한 설명을 조금 살펴보면, 파일 프로토콜을 나타내는 magic number와 아이템 개수(n) 를 파일버퍼에서 읽는다. 이 후 fromfile 메소드를 이용해 이어지는 바이트를 넘파이 배열로 읽는다. 여기서 struct.unpack() 메소드로 전달된 매개변수 값은 아래와 같이 나눌 수 있다.

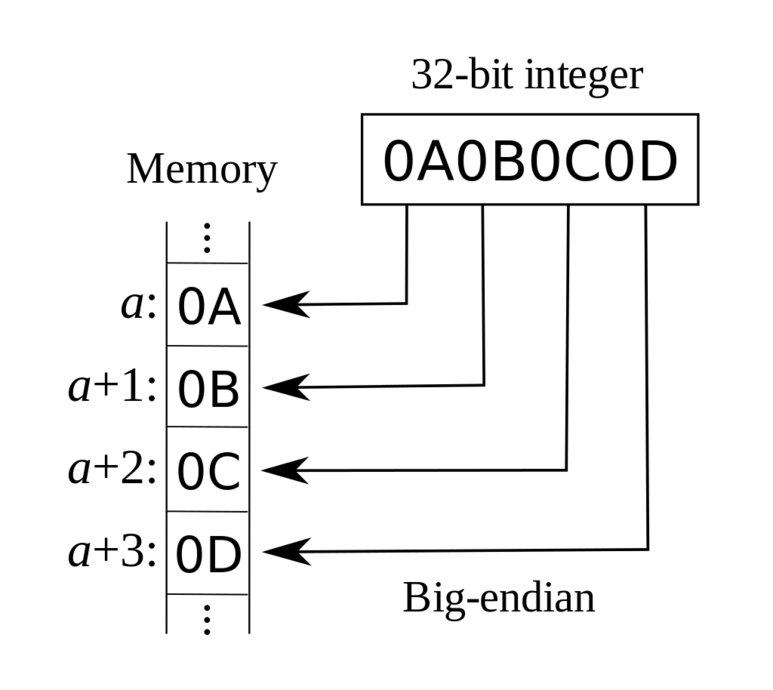
① > (Big Endian)
빅 엔디언을 나타낸다. 여기서 엔디언이란 바이트가 저장되는 순서를 의미하며, 컴퓨터의 메모리와 같은 1차원의 공간에 여러 개의 연속된 대상을 배열하는 방법이라고 할 수 있다. 엔디언에는 크게 빅 엔디언과 리틀 엔디언이 있는데, 이 중 빅 엔디언은 사람이 숫자를 쓰는 방법과 같이 큰 단위의 바이트가 앞에 오는 방법이다.

② I
부호가 없는 정수를 의미하며, 위의 코드에서는 II 이기 때문에 정수 2개가 온다는 것을 의미한다. 위의 과정으로 데이터를 로드하면, 이미지의 픽셀 값이 0 ~ 255 사이의 값을 갖는데, 이를 -1 ~ 1 사이의 값으로 정규화해준다.

이렇게 처리했을 때, 데이터를 읽고 전처리하는 오버헤드를 피할 수 있으며, 넘파이 배열을 사용하기 때문에 다차원 배열을 디스크에 저장하는 효율적인 방법 역시 사용할 수 있게 된다. numpy 의 savez() 함수를 사용하는 방법인데, pickle 모듈과 유사하다. 하지만 앞서 말한 것처럼 pickle 모듈보다는 넘파이 배열을 저장하는 데 최적화되어있다.
사용 방법은 아래와 같다.

[Python Code]

np.savez_compressed(
    'dataset/MNIST/mnist_scaled.npz',    # 압축 파일 경로
    X_train=x_train,                     # 학습 데이터
    Y_train=y_train,                     # 학습 데이터 실제 결과
    X_test=x_test,                       # 테스트 데이터
    Y_test=y_test                        # 테스트 데이터 실제 결과
)

주석에 언급한 것처럼 savez_compressed() 를 이용하면, 학습 및 테스트 데이터를 하나의 압축 파일로 생성할 수 있으며, 압축파일을 다시 읽을 때는 아래 코드처럼 np.load() 함수를 이용해서 불러오면 된다.

[Python Code]

mnist = np.load('dataset/MNIST/mnist_scaled.npz')
print(mnist.files)  # ['X_train', 'Y_train', 'X_test', 'Y_test']

x_train = mnist['X_train']
y_train = mnist['Y_train']
x_test = mnist['X_test']
y_test = mnist['Y_test']

(2) 역전파

전방향에 대한 연산으로 예측값을 산출했다면, 실제값과 비교했을 때 오차가 발생하게 된다. 신경망에서는 오차를 줄이기 위해 각 노드의 가중치에 대한 학습 및 업데이트 작업을 수행하는데 이를 역전파 과정이라고 한다.
우선 역전파 과정을 설명하기에 앞서 비용함수에 대한 개념을 알고 있어야한다. 비용함수란, 신경망이 예측을 얼마나 잘하는지에 대한 척도를 계산하는 함수로 손실함수라고도 부른다. 결과적으로 앞서 언급한 신경망의 오차를 계산하는 함수이며, 가중치를 학습 및 업데이트하는 작업은 비용함수 혹은 손실함수의 값이 줄어들도록 수정해야한다. 수정하는 방법은 그레디언트 하강(경사하강)법인데, 그레디언트는 비용함수의 미분을 이용하여 계산하게 된다. 예를 들어 아래와 같은 신경망이 있다고 가정해보자.

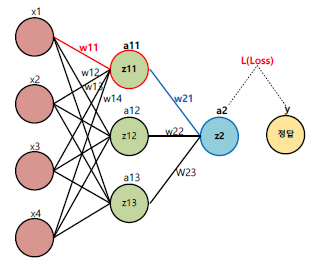
우선 이해를 좀 더 돕기 위해 각 층별로 1번째의 노드만을 대상으로 정방향 전파가 완료되었다고 하자. 그 때의 각 노드별 출력 값은 다음과 같다.

$ z_{11} = x_1 \cdot w_{11} + x_2 \cdot w_{12} + x_3 \cdot w_{13} + x_4 \cdot w_{14} $
$ z_2 = a_{11} \cdot w_{21} + a_{12} \cdot w_{22} + a_{13} \cdot w_{23} $
$ a_2 = z_2 $
$ L = (y - a_2)^2 $

우리가 계산해야되는 값은 w11 를 업데이트 하려는 값이며, 이는 손실함수를 업데이트하려는 가중치로 미분해줘야한다. 예시의 경우 최종적인 미분값은 $ \frac {\delta L} {\delta w_11} 이다.
하지만 위의 수식을 보면 알 수 있듯이, dL/dw11 을 한 번에 할 수 없으며, 하나의 수식으로 정리한다고 해도, 가능하지만 오히려 식이 더 복잡해져 미분을 하기에 어려워진다. 따라서 고등학교 수학에 나오는 개념 중 하나인 chain rule 방식을 적용해서 계산해보도록하자.
체인 룰은 단계별로 미분을 하고 이를 곱해서 최종적인 미분값을 구하는 방법이며, 위의 수식의 경우, 각 단계별 미분을 한 결과는 아래와 같다.

$ \frac {\delta z_{11}} {\delta w_{11}} = x_1 $
$ \frac {\delta a_{11}} {\delta z_{11}} = \sigma (z_{11}) \cdot (1 - \sigma (z_{11})) $
$ \frac {\delta z_2} {\delta a_{11}} = w_{21} $
$ \frac {\delta a_2} {\delta z_2} = 1 $
$ \frac {\delta L} {\delta a_2} = -2(y - a_2) $

이제 각 단계별로 미분값을 전부 곱해주면, 우리가 구하려했던 dL/dw11 에 대한 값이 나온다.

$ \frac {\delta z_{11}} {\delta w_{11}} \cdot \frac {\delta a_{11}} {\delta z_{11}} \cdot \frac {\delta z_2} {\delta a_{11}} \cdot \frac {\delta a_2} {\delta z_2} \cdot \frac{\delta L}{\delta a_2} = \frac {\delta L} {\delta w_{11}} $

정리를 하게 되면, dL/dw11 의 값은 다음과 같다.

$ \frac {\delta L} {\delta w_{11}} = x_1 \cdot \sigma (z_{11}) \cdot (1 - \sigma (z_{11})) \cdot w_{21} \cdot 1 \cdot (-2(y-a_2)) $

위와 같은 과정으로 모든 노드의 가중치를 업데이트 하게되고, 다시 정방향 전파를 통해 학습으로 예측값을 계산하는 방식으로 최적화를 수행하게된다. 단, 진행 속도는 학습률과 배치사이즈에 영향을 받기 때문에, 적절한 학습률과 배치 사이즈를 설정해주는 것이 매우 중요하다.

3) 코드 구현 : MLP

지금까지 살펴본 내용을 기반으로 MLP를 구현해보자. 코드는 첨부파일에 있는 MLP.py 파일을 참고하기바란다. 위의 코드를 프로젝트 내에 저장한 후 아래의 코드를 수행한다.

[Python Code]

from MLP import NeuralNetMLP

nn = NeuralNetMLP(
    n_hidden=100,
    l2=0.01,
    epochs=200,
    eta=0.0005,
    minibatch_size=100,
    shuffle=True,
    seed=1
)

nn._fit(
    x_train=x_train[:55000],
    y_train=y_train[:55000],
    x_valid=x_train[55000:],
    y_valid=y_train[55000:]
)

[실행 결과]

001/200 | 비용: 66739.71 | 훈련/검증 정확도 : 84.53%/88.86%
002/200 | 비용: 47830.40 | 훈련/검증 정확도 : 88.34%/91.74%
...
199/200 | 비용: 5100.21 | 훈련/검증 정확도 : 99.28%/98.10%
200/200 | 비용: 5065.78 | 훈련/검증 정확도 : 99.28%/97.98%

위의 결과와 유사하게 나온다면 학습이 완료되었다는 의미이며, 학습이 완료되면, 모델에서 사용된 비용함수와 모델의 정확도를 확인해보자.

[Python Code]

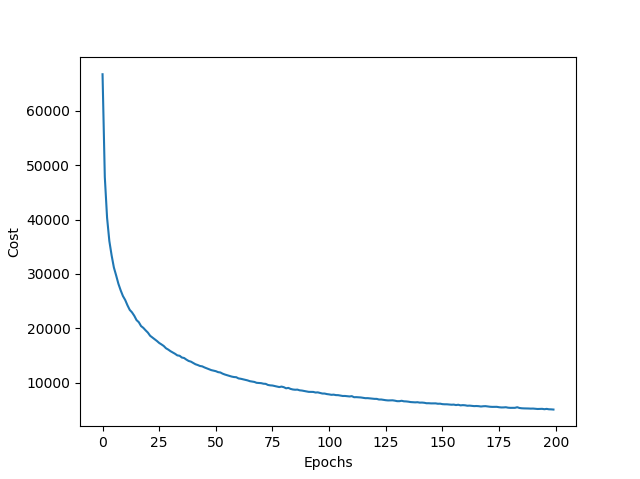
# 비용함수 출력
plt.plot(range(nn.epochs), nn.eval_['cost'])
plt.xlabel('Epochs')
plt.ylabel('Cost')
plt.show()

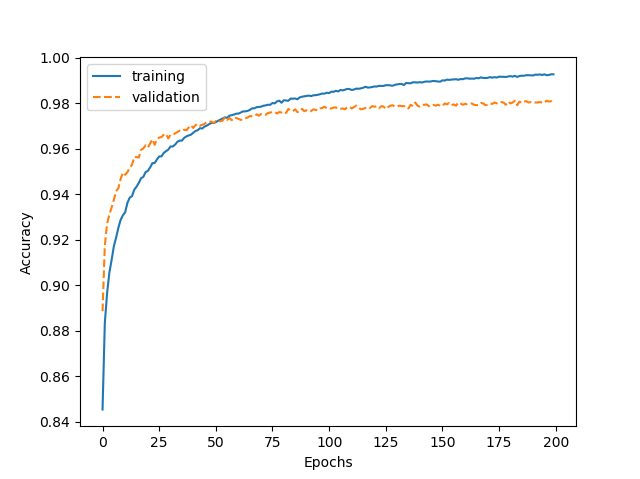
# 모델 정확도 출력
plt.plot(range(nn.epochs), nn.eval_['train_acc'], label='training')
plt.plot(range(nn.epochs), nn.eval_['valid_acc'], label='validation', linestyle='--')
plt.ylabel('Accuracy')
plt.xlabel('Epochs')
plt.legend()
plt.show()

[실행결과]

마지막으로 위 코드의 실제 예측 정확도를 계산해보자.

[Python Code]

y_test_pred = nn._predict(x_test)
acc = (np.sum(y_test == y_test_pred).astype(np.float) / x_test.shape[0])

print('테스트 정확도: %.2f%%' % (acc * 100))

[실행 결과]

테스트 정확도: 97.54%

[참고 자료]
http://blog.naver.com/PostView.nhn?blogId=qbxlvnf11&logNo=221386939202&parentCategoryNo=&categoryNo=52&viewDate=&isShowPopularPosts=false&from=postView