[Python Machine Learning] 7. 클러스터링

1. 클러스터링이란?

이전까지 회귀나 분류는 정답이 존재하는, 정확히는 반응변수, 결과변수가 존재하는 지도 학습이였다면, 클러스터링은 비지도 학습에 해당하는 대표적인 기법으로 훈련 데이터에 레이블이 부여되어있지 않다는 특징이 있다. 비지도 학습의 장점은 사용자도 모르는, 데이터 셋 내에 숨겨진 구조를 찾을 수 있다는 점이다.
이제부터 다뤄볼 클러스터링은 데이터를 각각의 군집으로 묶어서, 같은 군집의 요소들은 서로 비슷하도록, 다른 군집에 속한 것들은 달라지도록 하여 자연스러운 그룹을 찾는 기법이다.

2. K-Means

기법을 설명하기에 앞서 군집화를 먼저 이해할 필요가 있다. 군집은 비슷한 객체로 이루어진 그룹을 찾는 기법으로 앞서 설명한 것처럼, 한 그룹 안의 객체들은 다른 그룹에 있는 객체보다 더 관련이 많다. 대표적인 예로는 문서, 음악, 영화를 여러 주제의 그룹으로 모으는 경우가 있다.
군집화는 크게 프로토타입 기반, 계층적 군집, 밀집도 기반 군집으로 나눠볼 수 있는데 K-Means는 프로토타입 기반의 군집화에 속한다. 프로토타입 기반의 군집화에 대한 특징은 각 클러스터가 하나의 프로토타입으로 표현된다는 의미이다. 연속적인 특성에서는 비슷한 데이터 포인트가 센트로이드(평균)이거나, 범주형 특성에서는 메도이드(가장 대표가 되는 포인트 / 자주 등장하는 포인트)가 된다.

K-Means 기법에서 가장 중요한 것은 군집의 개수를 의미하는 k 에 대한 값을 적절히 설정해야 된다는 것인데, 뒤에서 다룰 엘보우 기법이나 실루엣 기법을 이용해서 적절한 k 값을 계산할 수 있다.

1) Scikit-Learn에서의 K-Means

[Python Code]

from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs

from matplotlib import pyplot as plt

x, y = make_blobs(n_samples=150, n_features=2, centers=3, cluster_std=0.5, shuffle=True, random_state=0)

plt.scatter(x[:, 0], x[:, 1], c='white', marker='o', edgecolors='black', s=50)
plt.grid()
plt.tight_layout()
plt.show()

kmeans = KMeans(n_clusters=3, init="random", n_init=10, max_iter=300, tol=1e-04, random_state=0)
pred = kmeans.fit_predict(x)

[실행 결과]

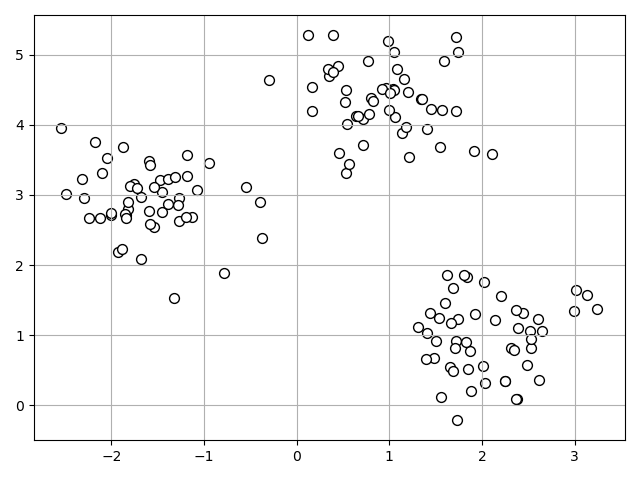
k-means 는 다음과 같이 4 단계로 요약할 수 있다.

① 샘플 포인트에서 랜덤하게 k개의 센트로이드를 초기 클러스터 중심으로 선택한다.
② 각 샘플을 가장 가까운 센트로이드 μ(j), j ∈{l, … ,k} 에 할당한다.
③ 할당된 샘플들의 중심으로 센트로이드를 이동한다.
④ 클러스터 할당이 변함 없거나, 사용자가 지정한 허용 오차나 최대 반복 횟수에 도달할 때까지 ②,③을 반복한다.

샘플간의 유사도는 거리의 반대 개념이고, 연속적인 특정을 가진 샘플을 클러스터로 묶는 데 널리 사용되는 거리는 m-차원 공간에 있는 두 포인트의 유클리디안 거리의 제곱으로 계산된다. 식은 다음과 같다.

$ d(x, y)^2 = \sum _{j=1}^m {(x_j - y_j)}^2 = {\Vert{x-y}\Vert}_2^2 $

위의 식을 기반으로 클러스터 내 제곱 오차합은 아래와 같이 계산하게 된다.

$ SSE = \sum _{i=1}^n \sum _{j=1}^m w^{(i, j)} = {\Vert{x^{(i)} - \mu ^{(j)}}\Vert}_2^2 $

위 식에서 μ 는 클러스터의 대표 포인트(센트로이드)를 의미한다. 만약 샘플 x 가 클러스터 j 내에 존재한다면 w(i,j) 는 1이 되고, 아니면 0이 된다.

다음으로 scikit-learn 에서의 KMeans 알고리즘 사용법을 살펴보자. 앞서 나온 코드에서도 확인할 수 있듯이, 아래의 내용과 같이 작성한다.

[Python Code]

from sklearn.cluster import KMeans

kmeans = KMeans( 
    n_clusters=3,
    init='random',
    n_init=10,
    max_iter=300,
    tol=1e-04,
    random_state=0
)

y_pred = kmeans.fit_predict(x)

결과로 산출된 군집을 확인해보면 아래의 시각화와 같다.

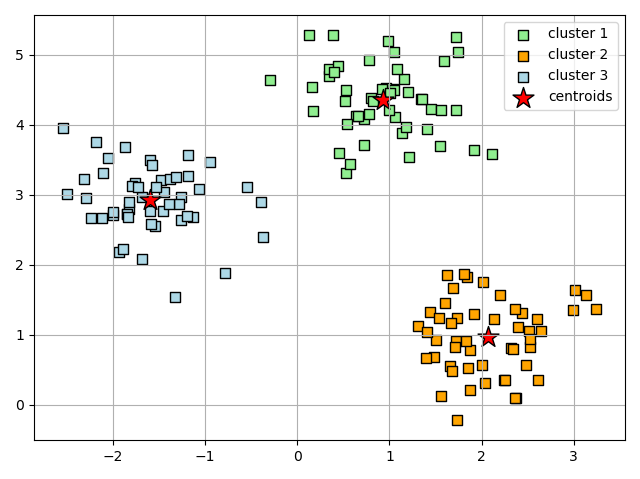
위의 산점도에서 k-means 알고리즘이 원형 중심부에 세 개의 센트로이드를 할당한 것을 확인할 수 있다. 보통 작은 데이터 셋에서는 잘 작동하지만, 사전에 군집의 개수인 k를 설정해줘야 된다는 단점이 있다.

2) K-Means++

앞서 살펴본 K-Means 의 경우 초기 센트로이드 값을 랜덤하게 설정하기 때문에 초기 값이 나쁠 경우 군집 결과까지 나쁜 군집으로 만들 수 있다. 이를 개선하기 위해서 고안된 알고리즘이 K-Means++ 이다. K-Means 와의 차이점은 초기 센트로이드가 서로 멀리 떨어지도록 위치시킨 후에 K-Means 군집화를 시작하게 하는 점이다. 자세한 과정은 아래 4단계로 정리할 수 있다.

① 선택한 k 개의 센트로이드를 저장할 빈 집합 M을 초기화한다.
② 입력 샘플에서 첫 번째 센트로이드 μ(i) 를 랜덤하게 선택하고 M에 할당한다.
③ M에 있지 않은 각 샘플 x(i) 에 대해 M에 있는 센트로이드까지 최소 제곱 거리를 찾는다.
④ 아래 식과 같은 가중치가 적용된 확률 분포를 사용하여 센트로이드 $ {\mu }^{(i)} $ 를 랜덤하게 선택한다.
     $ \frac {d({\mu }^{(p)}, M)^2} {\sum _{i} d{(x^2, M)}^2} $
⑤ k 개의 센트로이드가 나올때까지 ②와 ③을 반복한다.
⑥ 이 후 K-Means 를 수행한다.

사이킷런에서 KMeans 클래스로 K-Means++를 구현하려면 init 매개변수의 값을 “k-means++” 로 설정하면 된다. (실전에서 유용하기 때문에 기본값으로 지정되어 있다.) 코드는 다음과 같다.

[Python Code]

kmeans_plus = KMeans(n_clusters=3, init="k-means++", n_init=10, max_iter=300, tol=1e-04, random_state=0)
pred_plus = kmeans_plus.fit_predict(x)

3) 직접 군집화 vs. 간접 군집화

직접 군집화는 데이터셋의 샘플이 정확히 하나의 클러스터에 할당되는 알고리즘으로 대표적인 예시가 앞서 본 K-Means 이다. 반면, 간접 군집화는 샘플을 하나 이상의 클러스터에 할당하는 알고리즘이다. 대표적인 알고리즘으로는 퍼지 알고리즘이 해당된다. 앞서 K-Means에 대해 살펴봤기 때문에 이번에는 퍼지 알고리즘(Fuzzy C-Means) 를 살펴보자.
퍼지 알고리즘의 진행과정은 K-Means 와 매우 유사하지만, 포인트가 직접 클러스터에 할당되는 것이 아니라, 해당 클러스터에 속한 확률로 변환된다. 각 값은 확률이기 때문에 0 ~ 1사이의 값을 갖고, 각 클러스터 센트로이드의 확률을 의미한다. 또한 한 샘플에 대한 클래스 소속 확률의 합은 반드시 1이 되어야 한다. 알고리즘의 과정은 아래의 내용과 같다.

① 센트로이드 개수 k 를 지정하고 랜덤하게 각 포인트에 대해 클러스터의 확률을 할당한다.
② 클러스터 센트로이드 $ {\mu}^{(i)}, j ∈ { 1, … , k } $ 를 계산한다.
③ 각 샘플에 대해 클러스터 소속 확률을 계산한다.
④ 클러스터 확률에 변화가 없거나, 사용자가 지정한 허용오차 혹은 최대 반복 횟수에 도달하기 전까지 ②와 ③을 반복한다.

4) 최적의 K 값 찾기

(1) 엘보우 기법

비지도 학습의 단점은 정답을 모른다는 점이다. 데이터 셋에도 클래스 레이블이 없기 때문에 기존에 분류문제에서 사용하던 성능평가 방법을 사용하지 못한다는 것이다. 따라서 군집에 대한 평가를 하려면 알고리즘 자체에서 제공하는 지표를 활용해야만 한다. 앞서 본 K-Means 의 경우, 군집의 성능을 비교하려면, 각 군집 내 SSE(왜곡 혹은 관성) 를 사용한다. 또한 scikit-learn 에서는 KMeans 모델 학습 시에 inertia_ 속성에 계산 및 저장된다. 지금부터 알아볼 엘보우 기법은 군집의 SSE를 활용한 방법으로 그래프를 사용해 문제에 최적인 클러스터의 개수를 추정하는 기법이다.
일반적으로 k 값이 증가하면, 군집 내 왜곡은 줄어들 것이다. 이유는 샘플이 할당된 센트로이드에 가까워지기 때문이며, 엘보우 기법은 왜곡이 빠르게 증가하는 지점의 k 값을 찾는다. 자세한 내용은 아래 코드와 함께 살펴보도록 하자.

[Python Code]

print('왜곡 : %.2f' % kmeans_plus.inertia_)

distortions = []
for i in range(1, 11):
    kmeans_plus = KMeans(n_clusters=i, init='k-means++', n_init=10, max_iter=300, random_state=0)
    kmeans_plus.fit(x)
    distortions.append(kmeans_plus.inertia_)
    
plt.plot(range(1, 11), distortions, marker='o')
plt.xlabel('Number of clusters')
plt.ylabel('Distortion')
plt.tight_layout()
plt.show()

[실행결과]

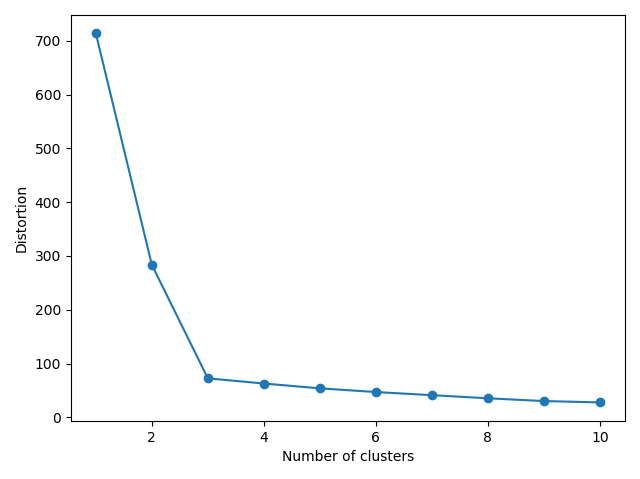
위 그림에 따르면 클러스터의 수가 3일 때 왜곡의 변화가 급격하게 일어났다는 것을 통해, 최적의 클러스터 수는 3개로 설정하면 된다는 결론을 얻을 수 있다.

(2) 실루엣 기법

실루엣 기법 역시 군집 분석에 대한 평가 기법중 하나로, 클러스터 내에 샘플들이 얼마나 조밀하게 모여있는지를 측정하는 그래프 도구이다. 이 때 각 데이터가 얼마나 조밀하게 모여있는 지를 나타내는 것이 실루엣 계수이며, 해당 기법에서 사용되는 실루엣 계수를 계산하려면 아래 3 단계를 적용하면 된다.

① 샘플 x(i) 와 동일한 클러스터 내 다른 포인트 사이의 거리를 모두 계산 후, 평균을 내어 클러스터 응집력(a(i))을 산출한다.
② 샘플 x(i) 와 가장 가까운 클러스터의 모든 샘플 간의 평균거리로 최근접 클러스터의 클러스터 분리도(b(i))를 계산한다.
③ 클러스터 응집력과 분리도 사이의 차이를 둘 중 큰 값으로 나누어 실루엣 s(i) 를 아래의 식으로 계산한다.

$s^{(i)} = \frac {b^{(i)} - a^{(i)}} {\max {b^{(i)}, a^{(i)}}}$

실루엣 계수는 일반적으로 -1 ~ 1 사이의 값을 가진다. 위의 식에서 만약 응집도 와 군집도가 같다면 실루엣 계수는 0이 된다. 반면 분리도 > 응집력 인 경우라면, 실루엣 계수는 1에 가까워지게 된다.
결과적으로 클러스터의 분리도란 샘플이 다른 클러스터와 얼마나 다른가를, 클러스터 응집력이란 하나의 클러스터 내에 요소들이 같은 클러스터 내의 다른 요소들과 얼마나 비슷한지를 나타낸다고 할 수 있다. scikit-learn 에서는 실루엣 기법을 사용하려면, metrics 이하에 silhouette_samples 함수를 이용하면 된다. 자세한 코드는 아래와 같다. 측정할 모델은 앞서 살펴본 K-Means++ 를 사용한다.

[Python Code]

import numpy as np
from matplotlib import cm
from sklearn.metrics import silhouette_samples

cluster_labels = np.unique(pred_plus)
n_clusters = cluster_labels.shape[0]
silhouette_vals = silhouette_samples(x, pred_plus, metric='euclidean')

y_ax_lower, y_ax_upper = 0, 0
yticks = []

for i, c in enumerate(cluster_labels):
    c_silhouette_vals = silhouette_vals[pred_plus == c]
    c_silhouette_vals.sort()
    y_ax_upper += len(c_silhouette_vals)
    color = cm.jet(float(i) / n_clusters)

    plt.barh(range(y_ax_lower, y_ax_upper),
             c_silhouette_vals,
             height=1.0,
             edgecolor='none',
             color=color)
    yticks.append((y_ax_upper + y_ax_lower) / 2.)
    y_ax_lower += len(c_silhouette_vals)

silhouette_avg = np.mean(c_silhouette_vals)

plt.axvline(silhouette_avg, color='red', linestyle='--')
plt.yticks(yticks, cluster_labels + 1)
plt.ylabel('Cluster')
plt.xlabel('Silhouette Coefficient')

plt.tight_layout()
plt.show()

[실행 결과]

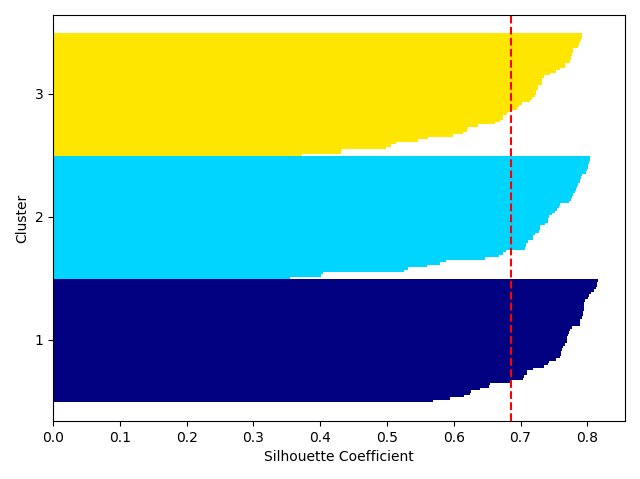
위의 그래프를 통해서 알 수 있듯이, 3개의 군집 모두 1에 가까운 실루엣 계수를 갖는 것으로 보아 군집이 잘 형성됬다고 볼 수 있다. 만약 군집화가 잘못된다면 어떤 형태일지 살펴보기 위해, k = 2로 설정하고 같은 코드를 수행하게 되면 아래의 결과와 유사한 형태로 나타날 것이다.

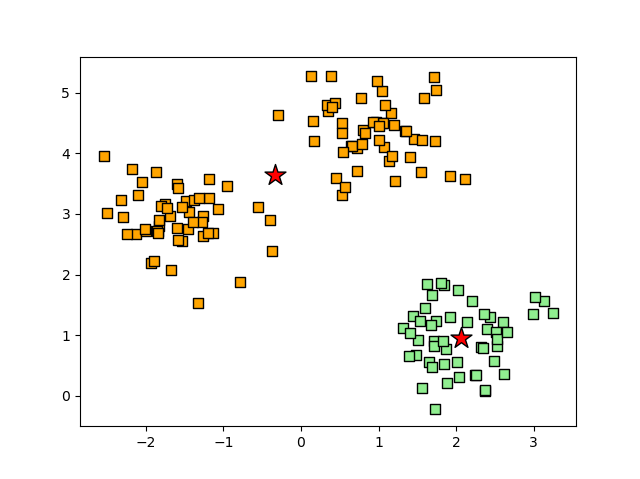
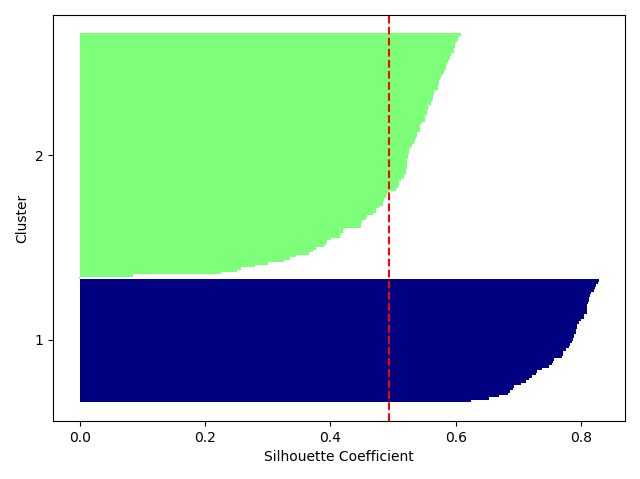
산점도에서는 2번 군집의 중심이 두 군집 사이에 위치한다고 예측했으며, 실루엣 그래프의 경우도 길이나 두께가 서로 확실히 다르다는 것이 확인된다.

3. 계층적 군집

계층적 군집은 프로토타입 기반의 군집 기법으로 이진트리형태의 덴드로그램을 그려서 군집화를 표현한다. 뿐만 아니라 K-Means 처럼 군집의 개수를 사전에 정의할 필요도 없다. 계층적 군집은 다시 군집화 방식에 따라 병합계층 군집화와 분할 계층 군집화로 나눌 수 있다. 분할 계층 군집화는 하나의 클러스터로 시작해서 하나의 샘플이 남을 때까지 군집화를 계속 분할해서 군집을 만드는 방법이다. 이와 반대로 병합 계층 군집은 각 샘플이 독립적인 클러스터가 되어 시작하며, 하나의 클러스터가 남을 때까지 가장 가까운 클러스터를 합치는 방법이다. 이번 절에서는 병합 클러스터링에 대해서 다룰 예정이다.

1) 병합 계층 군집 연결 방식

보통 병합 계층 군집을 사용하게 되면, 단일 연결과 완전 연결 중 하나를 사용해 각 샘플을 병합하게 된다. 단일 연결이란 클러스터 쌍에서 가장 비슷한 샘플간의 거리를 계산하여 거리가 가장 작은 두 클러스터를 계산한다. 완전 연결은 단일 연결 방식과 비슷하지만 클러스터 쌍에서 가장 많이 다른 샘플 간의 비교를 통해 병합을 수행하는 방식이다. 위의 2가지 연결방식 중에서 완전 연결에 대한 방법이라 가정하고 병합 계층 군집을 수행하면 아래의 과정을 반복하게 된다.

① 모든 샘플의 거리 행렬을 계산한다.
② 모든 데이터 포인트를 단일 클러스터로 표현한다.
③ 가장 많이 다른 샘플 사이 거리를 기록하여 가장 가까운 2개의 클러스터를 병합한다.
④ 유사도 행렬을 업데이트 한다.
⑤ 하나의 클러스터가 될 때까지, 1 ~ 4를 반복한다.

위의 과정을 코드로 표현하면 다음과 같다.

[Python Code]

import pandas as pd
import numpy as np

np.random.seed(12)
variables = ['x', 'y', 'z']
labels = ['ID_0', 'ID_1', 'ID_2', 'ID_3', 'ID_4']

x = np.random.random_sample([5, 3])*10
df = pd.DataFrame(x, columns=variables, index=labels)
df

[실행 결과]

x         y         z
ID_0  1.541628  7.400497  2.633150
ID_1  5.337394  0.145750  9.187470
ID_2  9.007149  0.334214  9.569493
ID_3  1.372093  2.838284  6.060832
ID_4  9.442251  8.527355  0.022592

2) 거리 행렬에서의 계층 군집 수행

입력에 사용할 거리 행렬에 대한 계산을 위해 scipy 의 spatial.distance 모듈 내에 있는 pdist() 를 사용한다. pdist() 는 축약된 거리 행렬을 반환해준다.

[Python Code]

from scipy.spatial.distance import pdist, squareform

row_dist = pd.DataFrame(squareform(pdist(df, metric='euclidean')), columns=labels, index=labels)
row_dist

[실행 결과]

ID_0       ID_1       ID_2       ID_3       ID_4
ID_0   0.000000  10.488008  12.400774   5.708900   8.396706
ID_1  10.488008   0.000000   3.694396   5.722693  13.080373
ID_2  12.400774   3.694396   0.000000   8.767847  12.588097
ID_3   5.708900   5.722693   8.767847   0.000000  11.573821
ID_4   8.396706  13.080373  12.588097  11.573821   0.000000

앞서 정의한 X, Y, Z 특성을 기반으로 데이텃의 모든 샘플 쌍에 대한 유클리디안 거리를 계산하였다. 이를 위해 pdist() 로 계산한 결과를 squareform() 함수의 입력으로 넣어 샘플 간 거리 대칭 행렬을 생성해주면 된다.
거리 대칭 행렬까지 계산했기 때문에, 다음으로 완전 연결 병합을 진행해보자. 이를 위해 scipy 의 cluster.hierachy 모듈에 있는 linkage 함수를 사용하여 계산해보자.

[Python Code]

from scipy.cluster.hierarchy import linkage
help(linkage)

[실행 결과]

Help on function linkage in module scipy.cluster.hierarchy:
linkage(y, method='single', metric='euclidean', optimal_ordering=False)
Perform hierarchical/agglomerative clustering.

    The input y may be either a 1d condensed distance matrix
    or a 2d array of observation vectors.
    
    If y is a 1d condensed distance matrix,
    then y must be a :math:`\binom{n}{2}` sized
    vector where n is the number of original observations paired
    in the distance matrix. The behavior of this function is very
    similar to the MATLAB linkage function.
    ...

내용이 길어 전부 다 담지 못했지만, 함수 사용법에 대한 내용을 살펴보면 다음과 같이 정리할 수 있다. 먼저 pdist() 함수로 계산된 축약 거리 행렬을 입력값으로 사용한다. 만약 pdist 축약 거리행렬이 없다면, linkage() 함수에 초기 데이터 배열을 전달하고 유클리디안 지표를 매개변수로 사용할 수 있다. 예시는 다음과 같다.

[Python Code]

from scipy.cluster.hierarchy import linkage

# 잘못된 방식
# - 아래 코드에서 row_dist 는 squareform() 을 통해 생성된 거리행렬이다.
# - 잘못된 이유는 linkage() 의 입력값으로 squareform() 으로 생성된 거리행렬을
#   사용할 수 없기 때문이다.
# row_clusters = linkage(row_dist, method='complete', metric='euclidean')

# 올바른 방식 1
row_clusters = linkage(df, method='complete', metric='euclidean')

# 올바른 방식 2
row_clusters = linkage(df.values, method='complete', metric='euclidean')

위와 같이 군집을 생성했을 때 분석한 결과는 다음과 같다.

[Python Code]

pd.DataFrame(
    row_clusters,
    columns=['row label 1', 'row label 2', 'distance', 'item no.'],
    index=['cluster %d' %(i+1) for i in range(row_clusters.shape[0])]
)

[실행 결과]

row label 1  row label 2   distance  item no.
cluster 1          1.0          2.0   3.694396       2.0
cluster 2          0.0          3.0   5.708900       2.0
cluster 3          4.0          6.0  11.573821       3.0
cluster 4          5.0          7.0  13.080373       5.0

또한 위의 결과를 통해 덴드로그램도 그릴 수 있다. hierarchy 모듈에서 dendrogram 을 import 하게 되면 사용할 수 있으며, 코드는 다음과 같다.

[Python Code]

from scipy.cluster.hierarchy import dendrogram
import matplotlib.pyplot as plt

row_dendrogram = dendrogram(row_clusters, labels=labels)
plt.tight_layout()
plt.ylabel('Euclidean Distance')
plt.show()

[실행 결과]

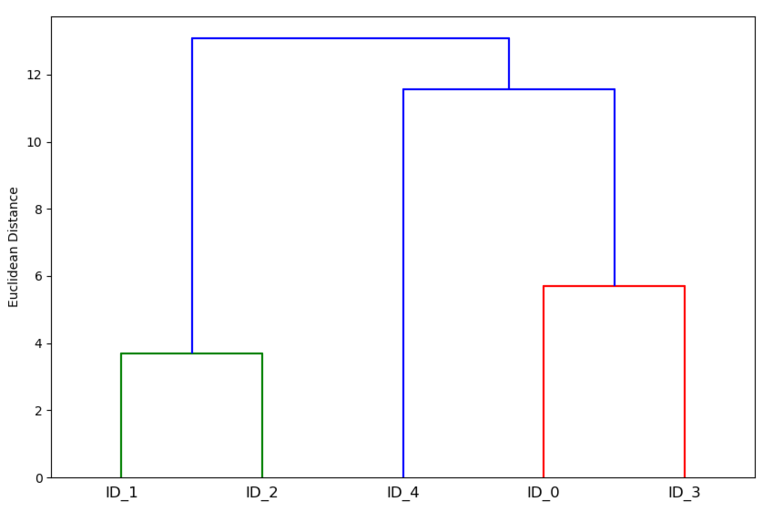
덴드로그램은 위의 그림처럼 병합 계측 군집이 수행되는 동안에 만들어지는 클러스터들을 요약해준다. 위의 경우 ID_1 과 ID_2 , ID_0 과 ID_4 가 서로 유클리디안 거리가 가까운 군집이라고 할 수 있다.

3) Scikit-Learn에서의 병합 군집

사이킷 런에서는 cluster 이하에 AgglomerativeClustering 클래스가 구현되어 있어, 원하는 클러스터 개수를 지정해 사용할 수 있다.

[Python Code]

from sklearn.cluster import AgglomerativeClustering

ac = AgglomerativeClustering(n_clusters=3, affinity='euclidean', linkage='complete')
labels = ac.fit_predict(x)

print("클러스터 레이블 : %s" % labels)

[실행 결과]

클러스터 레이블 : [0 1 1 0 2]

만약 앞서 본 예제를 수행하려면, n_cluster=2 로 설정하고 실행하면 된다.

[Python Code]

from sklearn.cluster import AgglomerativeClustering

ac = AgglomerativeClustering(n_clusters=2, affinity='euclidean', linkage='complete')
labels = ac.fit_predict(x)

print("클러스터 레이블 : %s" % labels)

[실행 결과]

클러스터 레이블 : 클래스 레이블 : [0 1 1 0 0]

앞서 설명한 것처럼 ID_0과 ID_4 는 같은 클러스터로, ID_1, ID_2 가 같은 클러스터로 배정 받았다. 또한 ID_3의 경우는 ID_1, ID_2 보다는 ID_0, ID_4와 유사한 클러스터로 배정 받았다는 것을 알 수 있다.