[Python Machine Learning] 6. 차원축소
1. 차원 축소란?
일반적으로 현실 세계의 문제는 가공되지 않은 데이터를 처리해야한다. 하지만 대부분의 머신러닝 모델의 경우 고차원의 데이터를 입력으로 사용하면 학습 속도가 느려지게 되고, 차원의 저주라고 해서 관측 단계와 메모리 사용이 기하급수적으로 증가하는 현상을 보인다. 뿐만 아니라, 과대적합의 위험성도 존재하여, 학습을 하는 전반적인 과정에서 어려움을 겪을 수 있다. 때문에 데이터에서 불필요한 정보들을 제거해줄 필요가 있는데, 이를 차원축소 라고 부른다.
2. 차원축소를 위한 접근법
구체적인 차원 축소 방법에는 투영과, 매니폴드 학습이라는 2가지가 존재한다.
1) 투영
현실적인 문제에서 훈련 샘플은 모든 차원에 걸쳐 균일하게 퍼져있는 경우는 희박하다. 많은 특성이 변화가 없거나 다른 특성들은 서로 강하게 연관되어 있다.
결과적으로 모든 훈련 샘플이 고차원 공간 내에 존재하는 저차원의 부분 공간에 놓여있다라고 할 수 있다.
예를 들어 아래 그림과 같은 3차원에 데이터가 원 모양으로 분포한다고 가정해보자.
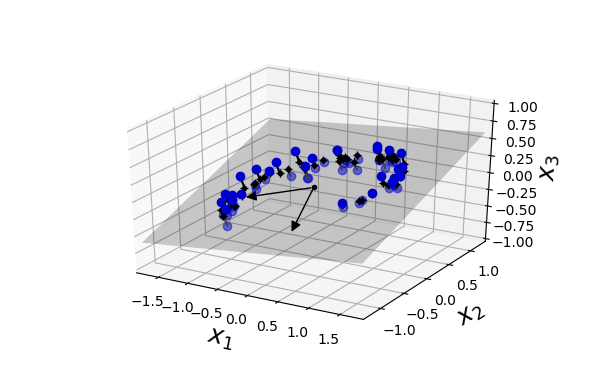
이 때 모든 샘플은 거의 평면인 상태로 놓여져 있으며, 그림에서 회색 사각형이 고차원 공간 내의 저차원 부분 공간이라고 가정해보자.
부분 공간을 기준으로 수직으로 바라보면 아래 그림과 같이 보일 것이다.
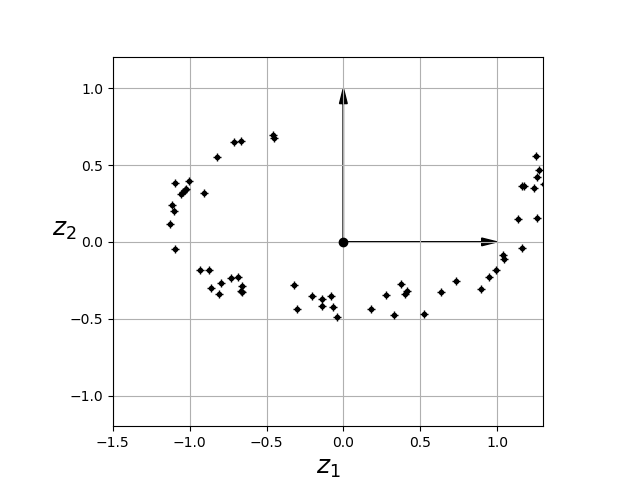
이렇게 원본 데이터는 특징이 3개가 존재하는 고차원의 데이터였지만 이를 특징이 2개인 부분 공간의 데이터로 변환함으로써 데이터의 분포를 이해하는 데에 수월하도록 차원을 줄이는 기법이 투영이다.
하지만 항상 좋은 것은 아닌게, 아래에 나온 스위스 롤과 같이 데이터셋의 공간이 뒤틀려 있거나, 휘어있는 경우에는 적용하는 것이 어렵다.
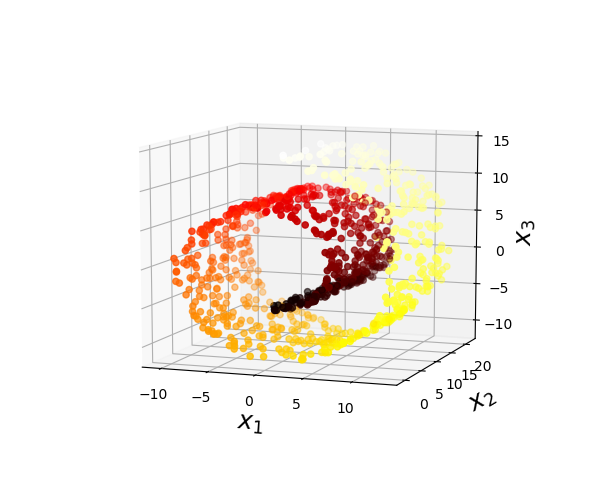
2) 매니폴드 학습
매니폴드란 고차원 공간에서 휘어지거나 뒤틀린 저차원 부분공간을 의미한다. 앞서 본 스위스롤 역시 매니폴드의 한 형태이다.
이를 일반화시키면, d 차원 매니폴드는 d 차원의 초평면으로 보일 수 있는 n 차원 공간의 일부이다. (단, d < n 이어야한다.)
그렇다면 매니폴드 학습은 다음과 같이 정의할 수 있다.
매니폴드 학습이란 많은 차원 축소 알고리즘이 훈련 샘플이 놓여있는 매니폴드를 모델링하는 식으로 작동한다. 이에 대한 전제 조건으로는 종종 암묵적으로 다른 가정과 병행되곤한다. 바로 처리해야할 작업이 저차원의 매니폴드 공간에 표현되면 더 간단해 질 수 있다는 의미이다. 앞서 본 스위스롤을 다시 한 번 살펴보자. 위의 스위스롤을 2차원으로 펼쳐보면 다음과 같다.
왼쪽은 결정경계가 복잡하게 보이지만, 오른쪽 그림은 결정경계가 단순한 직선으로 구분이 가능하다. 하지만 위와 같은 가정이 항상 유효한 것은 아니기 때문에 유의해야되는 부분이다.
정리를 해보자면, 모델을 훈련시키기 전에 훈련 세트의 차원을 감소시키면, 훈련 속도는 빨라지지만 항상 더 낫거나 간단한 솔루션이 되는 것은 아니다. 때문에 데이터 셋에 대한 의존도가 매우 높다고 할 수 있다.
3. PCA (주성분 분석, Principal Component Analysis)
가장 대표적인 차원 축소 알고리즘으로, 데이터에 가장 가까운 초평면을 정의한 다음 데이터를 평면에 투영시킨다.
1) 분산보존
저차원의 초평면에 훈련 데이터를 투영하기 전에 투영시키고자하는 초평면이 올바른지를 확인해야된다. 예를 들어 데이터의 분포가 아래의 그림과 같다고 가정해보자.
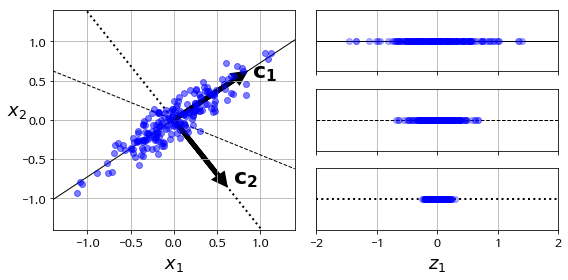
왼쪽의 그림이 데이터의 분포를 보여주는 것인데, 그래프 상에서도 알 수 있듯이, 총 3개의 축(선) 들로 구성되어 있으며, 이 중에서 실선에 투영된 것이 분산을 최대한으로 보존하는 반면, 점선에 투영되는 경우에는 상대적으로 분산이 매우 적다는 것을 알 수 있다. 이는 오른쪽 그래프를 통해서도 확인이 가능하다.
따라서 분산이 최대로 보존되는 실선을 축으로 선택하는 것이 정보를 가장 적게 손실할 수 있는 방법이 합리적이라고 할 수 있다.
2) 주성분
주성분 분석에서는 훈련 데이터의 분산이 최대가 되는 축을 찾는 것이 목적이다. (분산을 최대한 보존한다 = 정보의 손실이 가장 적다)
또한 첫 번째로 선정된 축과 수직이면서, 남은 분산을 최대한 보존하는 두번째 축을 찾는다. 위의 예제에서는 가운데 점선 축이 해당한다.
이 때, i 번째의 축을 정의하는 단위벡터를 i 번째 주성분 이라고 하며, 추출 단계는 다음과 같다.
① 데이터의 표준화 전처리
② 공분산 행렬 구성
③ 궁분산 행렬의 고유값과 고유 벡터 계산
④ 고유값을 내림차순으로 정렬해 고유 벡터의 순위를 계산
이렇듯, 고차원의 데이터인 경우 데이터셋에 존재하는 차원의 수만큼 이전 축에 직교하는 주성분의 축을 찾게 된다.
이런 주성분은 특잇값 분해(Singular Value Decomposition / SVD) 라는 표준행렬 분해기술을 이용하며, 학습 데이터 행렬인 X를 3개 행렬의 점곱으로 분해할 수 있다. 파이썬에서는 numpy 라이브러리에 있는 svd() 함수를 사용한다.
[Python Code]
import numpy as np
import pandas as pd
from sklearn.decomposition import PCA
# 데이터 생성
## 가중치 및 편향 설정
np.random.seed(4)
m = 60
w1, w2 = 0.1, 0.3
noise = 0.1
## 원본데이터 생성
## - 3차원의 데이터를 생성
angles = np.random.rand(m) * 3 * np.pi / 2 - 0.5
X = np.empty((m, 3))
X[:, 0] = np.cos(angles) + np.sin(angles)/2 + noise * np.random.randn(m) / 2
X[:, 1] = np.sin(angles) * 0.7 + noise * np.random.randn(m) / 2
X[:, 2] = X[:, 0] * w1 + X[:, 1] * w2 + noise * np.random.randn(m)
## SVD 과정
## -주성분이 2개인 것으로 가정
X_centered = X - X.mean(axis=0)
U, s, Vt = np.linalg.svd(X_centered)
c1 = Vt.T[:, 0]
c2 = Vt.T[:, 1]
위의 코드에서 X_centered에 대한 코드는 PCA에서 데이터셋의 평균을 0이라고 가정한다. 때문에 원점에 맞춰주기 위해서 X 대신 X_centered 값을 모델 생성시 사용한 것이다. 만약 위의 경우와 같이 PCA를 직접 구현하거나 혹은 다른 라이브러리를 사용하는 경우에는 데이터를 원점에 반드시 맞추고 구현한다.
다음으로 U, S Vt 에 대한 내용을 살펴보자. 앞서 언급한 대로 SVD를 계산하는 식은 아래와 같다고 볼 수 있다.
$ Cov = \frac{1} {n-1}X^TX $
$ = \frac{1} {n-1} (U \sum {V}^T)^T (U \sum {V}^T) $
$ = \frac{1} {n-1} (V \sum {U}^T)^T (U \sum {V}^T) $
$ = \frac{1} {n-1} V \sum ^2 {V}^T $
$ =V \frac {\sum ^2} {n-1} V^T $
따라서 U, s, Vt는 numpy.linalg.svd() 함수로부터 얻은 결과이며, 이 때 svd() 로 반환되는 값 중 V에 해당하는 값이 실제로는 위 식의 결과 중 VT 에 해당하는 부분이기 때문에 별도로 전치를 하였다. 그리고 이 중 첫번째 열과 두번째 열을 주성분으로 한다는 내용이 C1, C2 에 대입되는 값이다.
3) 투영하기
초평면은 분산을 가낭한 최대로 보존하는 부분공간이라고 할 수 있다. 또한 이 부분공간은 초기 d개의 주성분으로 정의하였기 때문에 원본 데이터의 차원을 d차원으로 축소할 수 있다고 앞서 언급했다.
투영을 하기위한 수학적인 방법은 행렬 X와 첫 d 개의 주성분을 담은 행렬 Wd를 점곱하면 된다.
$X_{d-\operatorname{proj}} = X \cdot W_d $
위의 식을 파이썬 코드로 나타내면 다음과 같다.
[Python Code]
W2 = Vt.T[:, 2]
X2D = X_centered.dot(W2)
print(X2D)
[실행결과]
[ 0.0138445 -0.15436525 -0.00722714 0.03418723 0.19736924 0.10140211
0.16431061 0.02056169 0.19288206 -0.03876721 -0.0321141 -0.1202656
0.02118536 0.10723273 -0.05582805 -0.05156738 -0.02954594 -0.04701266
-0.0432233 -0.12148596 0.11473492 -0.17523509 -0.0957267 0.03329202
0.10075862 -0.00704262 -0.04619367 0.00757823 -0.03667208 0.06609396
-0.06316965 -0.08520148 -0.06275083 0.01888076 0.11970735 0.13344465
-0.05719266 -0.15358232 -0.14626141 0.18311699 -0.05493836 0.02357194
0.17259078 -0.06236165 -0.0313641 -0.07531651 -0.11978326 0.07223271
0.08052131 -0.19394691 0.09538103 -0.03550105 0.00155054 0.01867136
-0.13964647 -0.02650672 -0.08812242 0.16582991 0.20294673 -0.00596072]
위의 결과와 함께 원천 데이터와도 비교를 해보자. 이 때 원본데이터는 X 가 아닌 원점에 맞춰진 X_centered 로 한다.
[Python Code]
print(X_centered.shape) # (60, 3)
print(X_centered[:, 0])
print(X_centered[:, 1])
print(X_centered[:, 2])
[실행결과]
[-1.03976771 -0.03178419 -0.9772388 -0.94419049 -0.78716483 1.09409378
...
0.21633176 1.08160954 -1.03558753 0.50112667 -1.11982458 0.56285699]
[-7.60238460e-01 3.90260570e-01 -6.73862060e-01 7.70779228e-04
...
-6.58809150e-01 4.37983062e-01 -3.78394231e-01 4.10942417e-01]
[-0.33288048 -0.03647667 -0.3207571 -0.04973041 0.11997074 0.2455515
...
0.00150316 0.07142462 -0.40664275 0.36668281 -0.01326584 0.18162183]
위와 같은 방법을 사이킷런에서는 PCA() 모델을 사용해 간단하게 구현할 수 있다.
[Python Code]
pca = PCA(n_components=2) # 차원을 2차원으로 줄이는 모델
x2d = pca.fit_transform(X) # 모델 학습
print(pca.components_)
[실행 결과]
[[-0.93636116 -0.29854881 -0.18465208]
[ 0.34027485 -0.90119108 -0.2684542 ]]
학습이 완료되면 모델내에 components_ 변수를 사용해 주성분을 확인할 수 있다. 이 때 주성분은 위의 실행결과에 나온 것처럼 행 벡터 형식으로 저장되어 있기 때문에 아래와 같이 전치를 시켜줘야한다.
[Python Code]
print(pca.components_.T)
[실행 결과]
[[-0.93636116 0.34027485]
[-0.29854881 -0.90119108]
[-0.18465208 -0.2684542 ]]
추가적으로 explained_variance_ratio_ 변수에 저장된 주성분의 설명된 분산 비율도 유용한 정보로 사용할 수 있다. 이는 각 주성분의 축을 따라 있는 데이터세의 분산 비율을 나타낸다.
아래와 같이 3차원 데이터셋의 처음 두 주성분에 대한 설명된 분산의 비율을 살펴보자.
[Python Code]
print(pca.explained_variance_ratio_)
[실행 결과]
[0.84248607 0.14631839]
4) 적절한 차원 수
축소할 차원 수는 충분한 분산이 될 때 까지 더해야 할 차원 수를 선택하는 것이 좋다. 또한 시각화까지 고려할 경우 차원을 2개나 3개로 줄이는 것이 일반적이다. 과정은 다음과 같다. 먼저 차원 축소 없이 PCA를 계산한 후, 훈련 데이터의 분산을 95%로 유지하는 데 필요한 최소한의 차원 수를 계산한다. 코드는 다음과 같다.
[Python Code]
from sklearn.decomposition import PCA
...
pca = PCA()
pca.fit(X_train)
cumsum = np.cumsum(pca.explained_variance_ratio_)
d = np.argmax(cumsum >= 0.95)
print(d, cumsum[d])
[실행 결과]
153 0.9504095236698549
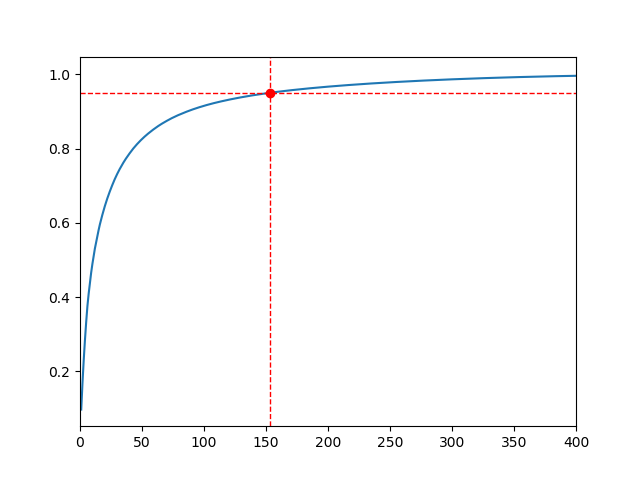
다음으로 PCA 모델의 매개변수중 하나인 n_components 값을 앞서 구한 d 로 설정하여 PCA 모델을 다시 만든다. 하지만 유지하려는 주성분의 수를 지정하기 보다는 보존하려는 분산의 비율을 n_components 값에 기입해주는 것이 더 좋으며, 값은 0.0 ~ 1.0 사이로 설정한다.
[Python Code]
pca = PCA(n_components=0.95)
X_reduced = pca.fit_transform(X_train)
print(pca.n_components_)
np.sum(pca.explained_variance_ratio_)
5) 압축을 위한 PCA
위의 과정을 통해서 알 수 있듯이, 차원을 축소하고 난 후에는 훈련 데이터 세트의 크기도 줄어들게 된다. 실제로 위의 예시를 수행하기전에는 784개의 특성을 갖고 있었지만, 차원이 축소되면서 153개로 줄어들었다. 즉, 분산은 유지되었으나, 데이터셋은 원본 크기의 약 20%가 된 것이다.
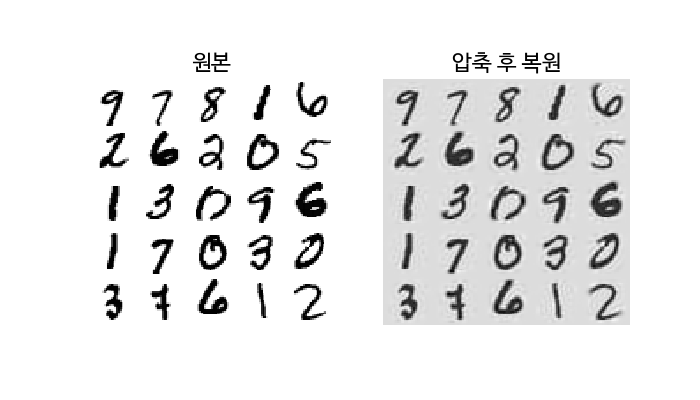
PCA 투영 변환을 반대로 적용하게 되면 차원을 되돌릴 수는 있다. 하지만 완벽하게 복원이 되기는 어려우며, 원본 데이터와 재구성된 데이터 간의 평균 제곱 거리만큼의 오차가 존재하게 된다. 이를 재구성 오차(Reconstruction Error) 라고 부른다.
아래의 코드를 통해서 비교해보자.
[Python Code]
pca = PCA(n_components=154)
X_reduced = pca.fit_transform(X_train)
X_recovered = pca.inverse_transform(X_reduced)
# mnist 이미지 출력 함수 선언
def plot_digits(instances, images_per_row=5, **options):
size = 28
images_per_row = min(len(instances), images_per_row)
images = [instance.reshape(size,size) for instance in instances]
n_rows = (len(instances) - 1) // images_per_row + 1
row_images = []
n_empty = n_rows * images_per_row - len(instances)
images.append(np.zeros((size, size * n_empty)))
for row in range(n_rows):
rimages = images[row * images_per_row : (row + 1) * images_per_row]
row_images.append(np.concatenate(rimages, axis=1))
image = np.concatenate(row_images, axis=0)
plt.imshow(image, cmap = matplotlib.cm.binary, **options)
plt.axis("off")
# 한글출력
plt.rcParams['font.family'] = 'NanumBarunGothic'
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['axes.labelsize'] = 14
plt.rcParams['xtick.labelsize'] = 12
plt.rcParams['ytick.labelsize'] = 12
# 시각화
plt.figure(figsize=(7, 4))
plt.subplot(121)
plot_digits(X_train[::2100])
plt.title("원본", fontsize=16)
plt.subplot(122)
plot_digits(X_recovered[::2100])
plt.title("압축 후 복원", fontsize=16)
plt.savefig("images/dimension_reduction/mnist_compression_plot")
6) 실습 : Wine 데이터 셋의 주성분 추출하기
실습의 과정은 다음과 같다.
① 데이터를 표준화 전처리한다.
② 공분산 행렬을 구성한다.
③ 공분산 행렬의 고유값과 고유 벡터를 구한다.
④ 고유값을 내림차순으로 정렬해 고유 벡터의 순위를 매긴다.
[Python Code]
# 실습 1: Wine Data 주성분 추출
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
# 데이터셋 로드
wine = pd.read_csv("https://archive.ics.uci.edu/ml/machine-learning-databases/wine/wine.data", header=None)
# 훈련, 테스트용 데이터 셋 각각 생성
x, y = wine.iloc[:, 1:].values, wine.iloc[:, 0].values
# 7:3 으로 데이터 split
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3, stratify=y, random_state=0)
# 표준화 처리
sc = StandardScaler()
x_train_std = sc.fit_transform(x_train)
x_test_std = sc.fit_transform(x_test)
# 공분산 계산
cov = np.cov(x_train_std.T) # 공분산 행렬 계산
eigen_vals, eigen_vector = np.linalg.eig(cov) # 고유값 분해 -> 고유 벡터, 고유값
print('고유값 \n%s' % eigen_vals)
total = sum(eigen_vals)
exp_val = [(i / total) for i in sorted(eigen_vals, reverse=True)]
cum_var_exp = np.cumsum(exp_val)
plt.bar(range(1, 14), exp_val, alpha=0.5, align='center', label='Individual Explained Varience')
plt.step(range(1, 14), cum_var_exp, where='mid', label='Cumulative Explained Varience')
plt.ylabel('Explained Varience Ratio')
plt.xlabel('Principal Component Index')
plt.legend(loc='best')
plt.tight_layout()
plt.show()
plt.savefig('images/dimension_reduction/Variance Sum to Component Index.png')
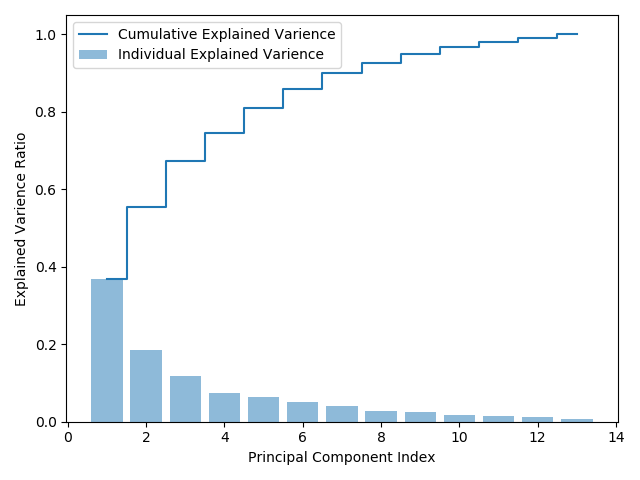
위의 결과그래프를 살펴보면 첫번째 주성분은 분산의 약 40%를 차지하고 있다는 것을 알 수 있으며, 첫 2개 주성분으로는 전체 분산의 약 60%를 설명할 수 있다.
다음으로 고유 벡터를 생성하고 투영해서 새로운 특성 부분 공간을 생성해보자.
[Python Code]
# 고유 벡터 - 고유값 쌍(튜플형식)으로 구성 후, 내림차순으로 정렬
eigen_pairs = [(np.abs(eigen_vals[i]), eigen_vector[:, i]) for i in range(len(eigen_vals))]
eigen_pairs.sort(key=lambda k: k[0], reverse=True)
print(eigen_pairs)
# 투영 행렬 W 생성
# 정렬된 것 중에서 가장 큰 고유값 2개와 쌍을 이루는 고유 벡터들을 선택한다. (전체 분산의 약 60% 정도를 사용할 것으로 예상됨)
# 투영 행렬은 13 x 2 형식의 리스트로 저장함
w = np.hstack((eigen_pairs[0][1][:, np.newaxis],
eigen_pairs[1][1][:, np.newaxis]))
print(w)
# PCA 부분공간 산출하기
# X' = XW ( 부분공간 : X' / X : 원본 , W : 투영행렬 )
# x_train_std[0].dot(w) # array([2.38299011, 0.45458499])
x_train_pca = x_train_std.dot(w)
# 변환된 훈련데이터의 시각화
colors = ['r', 'g', 'b']
markers = ['s', 'x', 'o']
for label, color, marker in zip(np.unique(y_train), colors, markers):
plt.scatter(x_train_pca[y_train==label, 0],
x_train_pca[y_train==label, 1],
c=color, label=label, marker=marker)
plt.xlabel('PC 1')
plt.ylabel('PC 2')
plt.legend(loc='lower left')
plt.tight_layout()
plt.show()
plt.savefig('images/dimension_reduction/wine_dim_reduction_result.png')
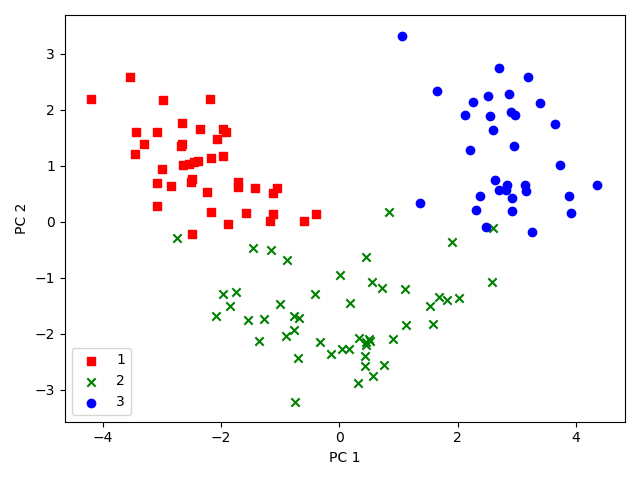
결과 그래프에서 확인할 수 있듯이, 데이터가 y축 보다 x축을 따라 더 넓게 퍼져있는 것을 확인할 수 있으며, 주성분은 고유값의 크기로 정렬했기 때문에 첫 번째 주성분이 가장 큰 분산을 갖는다는 것도 확인할 수 있다.
4. 커널 PCA
이전에 SVM에 대한 내용 중 샘플을 매우 높은 고차원의 특성 공간에서 암묵적으로 매핑해 SVM의 비선형 분류와 회귀를 가능하게 하는 커널 트릭에 대해서 이야기 했었다.
Python Machine Learning 3. 분류 : 서포트벡터머신(SVM)
고차원 특성 공간에서의 선형 결정 경계는 원본 공간에서 복잡한 비선형 결정 경계에 해당한다. 그리고 이러한 경계를 나눌 수 있게 하는 기법이 커널트릭 이라고 할 수 있다.
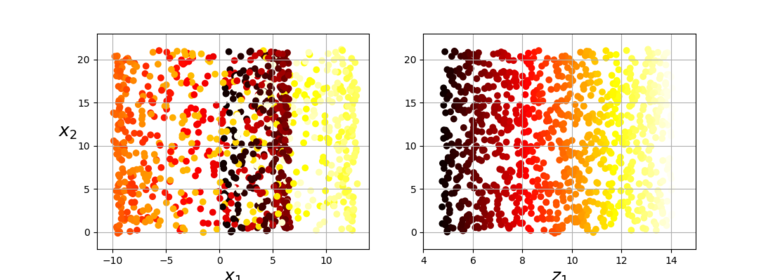
PCA 에서도 커널 트릭을 적용해 복잡한 비선형 투영으로의 차원 축소가 가능하며, 이를 kPCA(커널 PCA, kernel PCA) 라고 부른다. 이 기법은 맨처음에 잠깐 본 스위스롤 과 같은 매니폴드에 가까운 데이터셋을 대상으로 투영을 한 후 샘플의 군집을 유지하거나 펼칠 때 유용하게 사용할 수 있다.
사이킷 런에서의 커널 PCA 사용방법은 다음과 같다.
[Python Code]
from sklearn.decomposition import KernelPCA
rbf_pca = KernelPCA(n_components=2, kernel='rbf', gamma=0.04)
X_reduced = rbf_pca.fit_transform(X)
위와 같은 방법으로 앞서 본 스위스롤 데이터에 비선형 투영을 적용하면 아래의 그림과 같이 나오게 된다. 사용한 커널은 선형커널, RBF 커널, 시그모이드 커널을 사용했다.
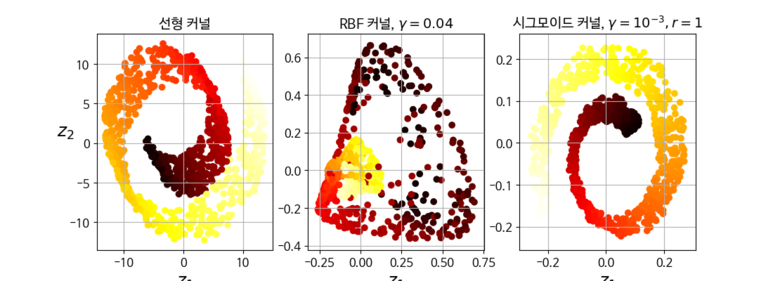
kPCA 는 비지도 학습으로 분류되기 때문에 좋은 커널과 하이퍼파라미터를 선택하기 위한 명확한 성능 측정 기준이 없다. 하지만 지도학습의 전처리 과정으로 사용되기 때문에 그리드 탐색을 사용해 최적의 커널과 하이퍼파라미터를 선택할 수 있다.
예시로는 앞서 살펴본 스위스롤 데이터셋으로 하며, 과정은 다음의 내용과 같다.
우선 2단계의 파이프라인으로 구성한다. 1단계에서는 kPCA를 이용해 3차원의 원본데이터를 2차원으로 축소하고 분류를 위해 로지스틱회귀를 사용한다.
2단계에서는 가장 높은 분류 정확도를 얻기 위해 GridSearchCV 를 사용하며, kPCA의 가장 좋은 커널과 gamma 파라미터 값을 산출한다.
마지막으로 가장 성능이 좋은 커널 및 하이퍼파라미터는 GridSearch 모델에서 제공하는 best_params_ 변수에 저장된다.
[Python Code]
from sklearn.model_selection import GridSearchCV
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import Pipeline
from sklearn.decomposition import KernelPCA
from sklearn.datasets import make_swiss_roll
import numpy as np
import pandas as pd
import matplotlib
import matplotlib.pyplot as plt
X, t = make_swiss_roll(n_samples=1000, noise=0.2, random_state=42)
y = t > 6.9
clf = Pipeline([
("kpca", KernelPCA(n_components=2)),
("log_reg", LogisticRegression(solver='liblinear'))
])
param_grid = [{
"kpca__gamma": np.linspace(0.03, 0.05, 10),
"kpca__kernel": ["rbf", "sigmoid"]
}]
grid_search = GridSearchCV(clf, param_grid, cv=3)
grid_search.fit(X, y)
print(grid_search.best_params_)
위의 과정 외에, 완전 비지도 학습 방법으로, 가장 낮은 재구성 오차를 만드는 커널과 하이퍼파라미터를 선택하는 방법도 있지만, PCA 만큼 쉽지 않다.
축소된 공간에 있는 샘플에 대해 선형 PCA를 역전시키면 재구성된 데이터 포인트는 원본 공간이 아닌 특성 공간에 놓이게 된다. 특성 공간은 무한 차원이기 때문에 재구성된 포인트를 계산할 수 없고, 재구성에 따른 실제 에러를 계산할 수 없다.
하지만 재구성된 포인트에 가깝게 매핑된 원본 공간의 포인트를 찾을 수 있으며, 해당 포인트를 가리켜 재구성 원상이라 한다.
원상을 산출하게 되면 원본 샘플과의 제곱거리를 측정할 수 있게 된다. 결과적으로 재구성 원상의 오차를 최소화하는 커널과 하이퍼파라미터를 선택할 수 있게 된다.
재구성을 하는 방법은 투영된 샘플을 훈련 세트로, 원본 샘플을 타겟으로 하여, 지도학습 중 회귀모델을 훈련시키는 방법이다. 사이킷런에서는 아래와 같은 방법으로 수행할 수 있다.
[Python Code]
rbf_pca = KernelPCA(n_components=2, kernel="rbf", gamma=0.0433, fit_inverse_transform=True)
X_reduced = rbf_pca.fit_transform(X)
X_preimage = rbf_pca.inverse_transform(X_reduced)
위의 코드에서 kPCA 모델 생성 시, fit_inverse_transform 파라미터 값을 True 로 설정해야 모델의 inverse_transform() 메소드를 사용할 수 있으며, 만약 설정 없이 아래의 에러 메세지가 나온다면 확인하기 바란다.
추가적으로 fit_inverse_transform 파라미터의 기본값은 False 이며, 이럴 경우 inverse_transform() 메소드는 생성되지 않는다.
sklearn.exceptions.NotFittedError: The fit_inverse_transform parameter was not set to True when instantiating and hence the inverse transform is not available.
마지막으로 재구성 원상 오차를 계산해보면 다음과 같이 나온다.
[Python Code]
from sklearn.metrics import mean_squared_error
print("MSE between original to prediction : ", mean_squared_error(X, X_preimage))
[실행 결과]
MSE between original to prediction : 32.78630879576615
5. 지역 선형 임베딩 (LLE, Locally Linear Embedding)
비선형 차원 축소 기법으로 투영에 의존하지 않는 매니폴드 학습이다. 이전 알고리즘과는 달리 각 훈련 샘플이 가장 가까이 위치한 이웃과 얼마나 선형적으로 연관이 있는가를 측정한다.
이는 국부적인 관계가 가장 잘 보존된 훈련 세트의 저차원 표현을 찾는 것과 같다. 특히 잡음이 심하지 않은 경우 꼬인 매니폴드를 펼치는 데에 잘 작동한다.
알고리즘의 과정은 다음과 같다.
① 각 훈련 샘플 X(i) 에 대해 가장 가까운 샘플 k개를 찾는다.
② 이웃에 대한 선형 함수로 X(i) 를 재구성한다.
③ 이 때 X(i) 와 ∑j=1m wi,j X(i) 사이의 제곱 거리가 최소가 되도록 하는 Wi,j 를 찾는다. 만약 X(j) 가 X(i) 의 가장 가까운 이웃 k 개에 포함되지 않는다면 Wi,j = 0 이 된다. 또한 각 훈련 샘플 X(i) 에 대한 가중치는 정규화 되어 있어야한다.
④ 앞선 단계를 거치게 되면 가중치 행렬 W 는 훈련 샘플 사이에 있는 지역 선형 관계를 갖는다. 따라서 관계가 보존되도록 훈련 샘플을 d차원 공간으로 매핑한다.
사이킷런에서는 아래와 같이 LLE 알고리즘을 사용할 수 있다.
[Python Code]
from sklearn.manifold import LocallyLinearEmbedding
lle = LocallyLinearEmbedding(n_components=2, n_neighbors=10)
X_reduced = lle.fit_transform(X)
6. 선형 판별 분석(Linear Discriminant Analysis)
규제가 없는 모델에서 차원의 저주로 인한 과대적합을 줄이고 계산 효율성을 높이기 위해서 사용되는 특성 추출 기법이다.
PCA와 매우 유사하지만, 지도학습 기법이기 때문에 분류 작업에서 더 뛰어난 특성 추출 기법이라고 볼 수 있다. 또한 데이터가 정규분포라고 가정하며, 클래스가 동일한 공분산 행렬을 갖는 샘플은 서로 통계적으로 독립적이라고 가정한다.
1) 과정
LDA의 주요 단계들은 다음과 같다.
① d 차원의 데이터셋을 표준화 전처리한다.
② 각 클래스에 대해 d 차원의 평균 벡터를 계산한다.
③ 클래스 간의 산포 행렬인 SB 와 클래스 내의 산포 행렬인 SW 로 구성된다.
④ SB 와 SW 행렬의 고유 벡터와 고유값을 계산한다.
⑤ 고유값을 내림차순으로 정렬하여 고유 벡터의 순서를 매긴다.
⑥ 고유값이 가장 큰 k개의 고유 벡터를 선택하여 d x k차원의 변환 행렬인 W를 구성한다.
⑦ 변환행렬 W를 사용해 샘플의 새로운 특성 부분 공간으로 투영한다.
2) 산포 행렬 계산
앞서 과정에서 언급한 것처럼 클래스 간의 산포행렬과 클래스 내의 산포행렬 모두 평균 벡터를 계산하여 구성된다.
이 때, 평균 벡터는 클래스 i의 샘플에 대한 특성의 평균값을 저장한다.
실습에 사용할 데이터는 앞서 실습한 Wine 데이터를 사용하며, 데이터의 표준화는 앞선 실습에서의 데이터 표준화 부분과 동일하게 진행한다.
클래스의 갯수가 총 3개(1~3) 이며, 1부터 시작하기 때문에 range(1, 4) 로 label 을 표현하였다.
[Python Code]
# 실행전 y 의 label 갯수 확인
y_label = set(y_train)
print(y_label) # 1 ~ 3
np.set_printoptions(precision=4) # 부동소수점, Array, 기타 numpy 객체가 표시되는 방식을 설정함
mean_vecs =[]
for label in range(1, 4):
mean_vecs.append(np.mean(x_train_std[y_train == label], axis=0)) # 각 label 별 평균값을 계산
print("Mean Vector %s : %s\n" % (label, mean_vecs[label-1]))
[실행 결과]
Mean Vector 1 : [ 0.9066 -0.3497 0.3201 -0.7189 0.5056 0.8807 0.9589 -0.5516 0.5416
0.2338 0.5897 0.6563 1.2075]
Mean Vector 2 : [-0.8749 -0.2848 -0.3735 0.3157 -0.3848 -0.0433 0.0635 -0.0946 0.0703
-0.8286 0.3144 0.3608 -0.7253]
Mean Vector 3 : [ 0.1992 0.866 0.1682 0.4148 -0.0451 -1.0286 -1.2876 0.8287 -0.7795
0.9649 -1.209 -1.3622 -0.4013]
산포 행렬은 평균 벡터를 이용해 아래의 식으로 표현할 수 있다.
$ S_W = \sum _{i=1}^C S_i $
위의 식을 파이썬 코드로 표현하면 다음과 같다.
[Python Code]
d = 13 # 특성 계수
Sw = np.zeros((d, d))
for label, mv in zip(range(1, 4), mean_vecs):
class_scatter = np.zeros((d, d))
for row in x_train_std[y_train == label]:
row, mv = row.reshape(d, 1), mv.reshape(d, 1)
class_scatter += (row - mv).dot((row - mv).T)
Sw += class_scatter
print("클래스 내의 산포 행렬 : %s x %s" % (Sw.shape[0], Sw.shape[1]))
print('클래스 레이블 분포 : %s' % np.bincount(y_train)[1:])
[실행 결과]
클래스 내의 산포 행렬 : 13 x 13
클래스 레이블 분포 : [41 50 33]
개별 산포 행렬 Si 를 산포행렬 Sw 로 모두 더하기 전에 스케일을 조정해야한다. 산포행렬을 클래스 샘플 개수로 나누면 산포 행렬을 계산하는 것이 공분산 행렬을 계산하는 것과 같다.
결과적으로 공분산 행렬은 산포행렬의 정규화라고 할 수 있다.
[Python Code]
Sw = np.zeros(((d, d)))
for label, mv in zip(range(1, 4), mean_vecs):
class_scatter = np.cov(x_train_std[y_train == label].T, bias=True)
Sw += class_scatter
print("스케일 조정된 클래스 내의 산포 행렬 : %s x %s" % (Sw.shape[0], Sw.shape[1]))
[실행 결과]
스케일 조정된 클래스 내의 산포 행렬 : 13 x 13
다음으로 클래스 간의 산포행렬인 SB 를 계산한다.
[Python Code]
mean_class = np.mean(x_train_std, axis=0)
mean_class = mean_class.reshape(d, 1)
S_B = np.zeros((d, d))
for i, mean_vec in enumerate(mean_vecs):
n = x_train[y_train == i + 1, :].shape[0]
mean_vec = mean_vec.reshape(d, 1)
S_B += n * (mean_vec - mean_class).dot((mean_vec - mean_class).T)
print("클래스 간 산포행렬 : %s x %s" % (S_B.shape[0], S_B.shape[1]))
[실행결과]
클래스 간 산포행렬 : 13 x 13
3) 새로운 특성부분 공간을 위한 선형 판별 벡터 생성 및 반영
이 후 과정은 PCA와 유사하게, 행렬 Sw-1SB 를 계산해주면 된다.
[Python Code]
eigen_vals, eigen_vecs = np.linalg.eig(np.linalg.inv(Sw).dot(S_B))
eigen_pairs = [(np.abs(eigen_vals[i]), eigen_vecs[:, i]) for i in range(len(eigen_vals))]
eigen_pairs = sorted(eigen_pairs, key=lambda k: k[0], reverse=True)
print("내림차순 고유값\n")
for eigen_val in eigen_pairs:
print(eigen_val[0])
[실행결과]
내림차순 고유값
358.00420701336594
177.07768640666228
2.897788744761761e-14
2.842170943040401e-14
1.9861923711452444e-14
1.969800906168211e-14
1.969800906168211e-14
1.8105958343606454e-14
1.4708272757021412e-14
8.653798256529554e-15
8.653798256529554e-15
3.4503200980472656e-15
8.922969632820571e-17
LDA에서 선형판별벡터의 길이는 (클래스개수 - 1)개 이다. 클래스 내 산포행렬인 SB 가 랭크 1또는 그 이하인 클래스 개수 만큼의 행렬을 합한 것이기 때문이다. 이를 그래프로 살펴보면 아래와 같다.
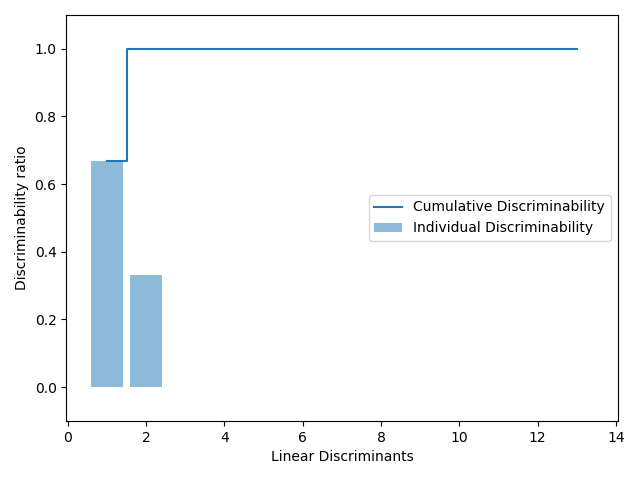
마지막으로 2개의 판별 고유 벡터를 열로 쌓은 변환 백터 W를 생성하고 이를 훈련 데이터 곱해서 데이터를 변환시켜보자.
[Python Code]
W = np.hstack((eigen_pairs[0][1][:, np.newaxis].real,
eigen_pairs[1][1][:, np.newaxis].real))
print("행렬 W:\n", W)
x_train_lda = x_train_std.dot(W)
colors = ['r', 'b', 'g']
markers = ['s', 'x', 'o']
for l, c, m in zip(np.unique(y_train), colors, markers):
plt.scatter(
x_train_lda[y_train==l, 0],
x_train_lda[y_train==l, 1] * (-1),
c=c, label=l, marker=m
)
plt.xlabel("LD 1")
plt.ylabel("LD 2")
plt.legend(loc="lower right")
plt.tight_layout()
plt.show()
[실행결과]
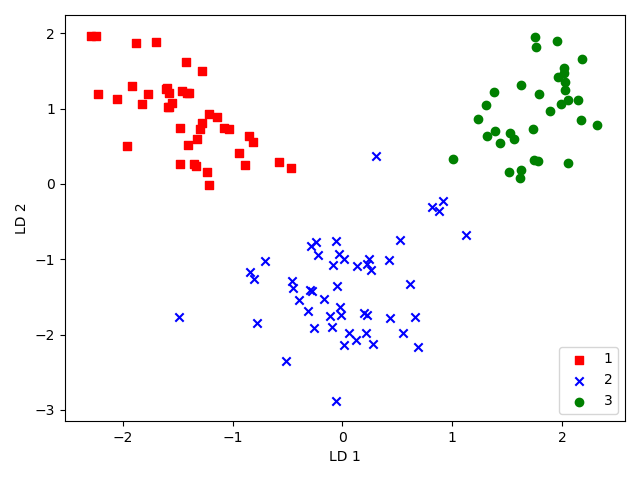
4) Scikit-Learn 을 이용한 LDA
앞서 설명한 모든 과정을 scikit-learn 의 LDA() 를 사용하면 단순하고, 쉽게 계산하는 것이 가능하다
추가적으로 변환된 데이터를 이용해 로지스틱 회귀로 예측해보자.
[Python Code]
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA
from sklearn.linear_model import LogisticRegression
import matplotlib
import matplotlib.pyplot as plt
import matplotlib.font_manager as fm
from matplotlib.colors import ListedColormap
lda = LDA(n_components=2)
x_train_lda = lda.fit_transform(x_train_std, y_train)
def plot_decision_regions(x, y, classifier, test_idx=None, resolution=0.02):
markers = ('s', 'x', 'o', '^', 'v')
colors = ("red", "blue", "lightgreen", "gray", "cyan")
cmap = ListedColormap(colors[:len(np.unique(y))])
x1_min, x1_max = x[:, 0].min() - 1, x[:, 0].max() + 1
x2_min, x2_max = x[:, 1].min() - 1, x[:, 1].max() + 1
xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution),
np.arange(x2_min, x2_max, resolution))
z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
z = z.reshape(xx1.shape)
plt.contourf(xx1, xx2, z, alpha=.3, cmap=cmap)
plt.xlim(xx1.min(), xx1.max())
plt.ylim(xx2.min(), xx2.max())
for idx, cl in enumerate(np.unique(y)):
plt.scatter(x = x[y == cl, 0], y = x[y == cl, 1],
alpha=0.8, c=colors[idx], marker=markers[idx],
label=cl, edgecolors="black")
if test_idx:
x_test, y_test = x[test_idx, :], y[test_idx]
plt.scatter(x_test[:, 0], x_test[:, 1],
c='', edgecolors="black", alpha=1.0,
linewidth=1, marker="o",
s=100, label="test set")
lr = LogisticRegression(solver="liblinear", multi_class="auto")
lr = lr.fit(x_train_lda, y_train)
plot_decision_regions(x_train_lda, y_train, classifier=lr)
[실행결과]
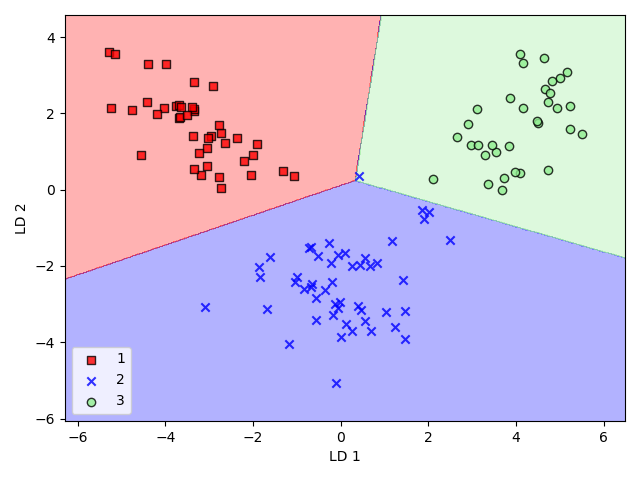
확인해본 결과 클래스 2로 분류된 1개 데이터만 오분류했다는 것을 알 수 있었으며, 규제 강도를 낮추면, 정확히 분류해 낼 것으로 보인다.
다음으로 모델에 테스트 데이터를 넣고 예측해보자.
[Python Code]
x_test_lda = lda.transform(x_test_std)
plot_decision_regions(x_test_lda, y_test, classifier=lr)
plt.xlabel("LD 1")
plt.ylabel("LD 2")
plt.legend(loc="lower left")
plt.tight_layout()
plt.show()
[실행결과]
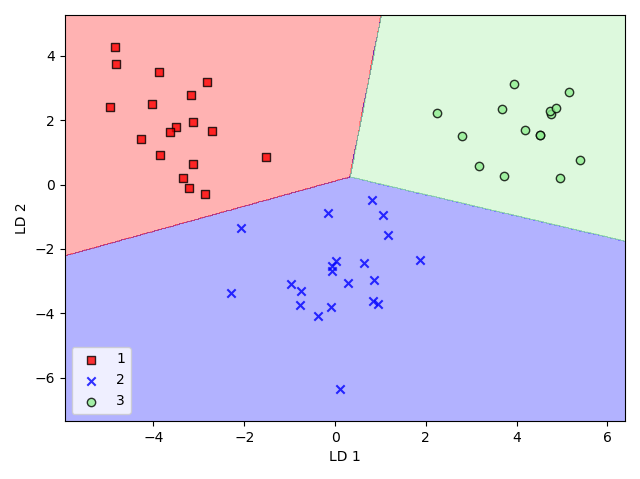
테스트 셋의 결과 원본 13개의 와인특성 대신 2차원의 특성부분공간을 이용해 정확히 분류해낸다는 것을 확인할 수 있다.

댓글남기기