[Python Machine Learning] 2. 회귀

1. 회귀

영국의 유전학자 갈튼이 생각한 문제로, 출력 변수와 입력변수가 선형관계를 가정하는 단순한 통계 분석 기법으로 하나 이상의 특성과 연속적인 타깃 변수 사이의 관계를 모델링 하는 것이다.
단변량 회귀와 다변량 회귀로 종류를 나눠볼 수 있으며, 일반적인 머신러닝 문제들은 다변량 회귀(다항회귀)로 접근한다.

1) 단변량 회귀

하나의 특성(설명변수) 와 연속적인 타깃(응답변수) 사이의 관계를 모델링한다. 선형 모델에 대한 식은 다음과 같다.

$y\ =\ {w}_0\ +\ {w}_1x $

위의 식에서 y 는 목표변수를, w0 는 y 축 절편을, w1 은 특성의 가중치를 의미하고 x는 특성을 의미한다.

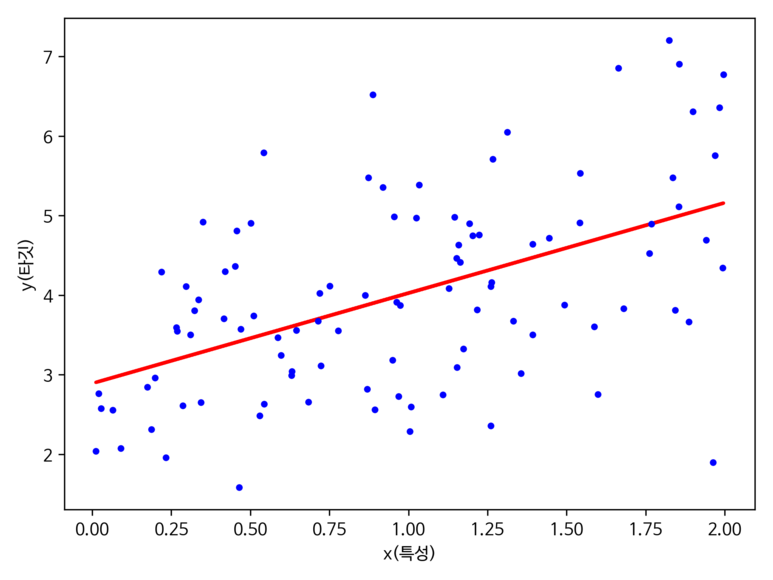
• 회귀 직선 : 데이터에 가장 잘 맞는 직선
• 오프셋(또는 잔차) : 회귀 직선과 샘플 포인트 사이의 직선 거리

위의 시각화에 대한 코드는 아래와 같다.

[Python Code]

x = 2 * np.random.rand(100, 1)
y = 3 + x + np.random.randn(100, 1)

lin_reg = LinearRegression()
lin_reg.fit(x, y)
y_pred = lin_reg.predict(x)

plt.plot(x, y_pred, "r-", linewidth=2)
plt.plot(x, y, "b.")
plt.xlabel("x(특성)")
plt.ylabel("y(타깃)")
plt.show()

2) 다변량 회귀

단변량 회귀를 여러 개의 특성이 있는 경우로 일반화(확장) 한 개념이다.

$\ y\ =\ {w}0\ {x}_0\ +\ {w}_1\ {x}_1\ + …\ +\ {w}_m\ {x}_m\ =\ m\ {∑}{i=0}{w}_i\ {x}_i = {w}^T\x $

하지만 3개의 특성을 갖고 있어도 3차원 산점도를 이해하는 것은 어렵다.

3) 실습 1: 주택 데이터 분석

우선 단변량 회귀에 대해서 예제로 좀 더 살펴보자. 사용할 데이터 셋은 UCI 머신 러닝 저장소에 공개되었던 주택 데이터를 이용할 것이다.

housing.data.txt 파일

데이터를 살펴보면 다음과 같다.

[Python Code]

df = pd.read_csv("data/housing.data.txt", header=None, sep='\s+')
df.columns = ["CRIM", "ZN", "INDUS", "CHAS", "NOX", "RM", "AGE",\
    "DIS", "RAD", "TAX", "PTRATIO", "B", "LSTAT", "MEDV"]
df.head()

Out[24]:
CRIM    ZN  INDUS  CHAS    NOX  ...    TAX  PTRATIO       B  LSTAT  MEDV
0  0.00632  18.0   2.31     0  0.538  ...  296.0     15.3  396.90   4.98  24.0
1  0.02731   0.0   7.07     0  0.469  ...  242.0     17.8  396.90   9.14  21.6
2  0.02729   0.0   7.07     0  0.469  ...  242.0     17.8  392.83   4.03  34.7
3  0.03237   0.0   2.18     0  0.458  ...  222.0     18.7  394.63   2.94  33.4
4  0.06905   0.0   2.18     0  0.458  ...  222.0     18.7  396.90   5.33  36.2

각 컬럼의 의미하는 내용은 다음과 같다.

• CRIM : 도시 인당 범죄율
• ZN : 25,000 평방피트가 넘는 주택
• INDUS : 도시에서 소매 업종이 아닌 지역의 비율
• CHAS : 찰스 강 인점 여부(1 = 인접 , 0 = 그 외)
• NOX : 일산화탄소 농도(per 100ppm)
• RM : 주택의 평균 방 갯수
• AGE : 1940 년 이전에 지어진 자가 주택 비율
• DIS : 5개의 보스턴 고용 센터까지의 가중치가 적용된 거리
• RAD : 방사형으로 뻗은 고속도로 까지의 접근성 지수
• TAX : 10만 달러당 재산세율
• PTRATIO : 도시의 학생-교사 비율
• B : 1000(Bk - 0.63)2 , Bk = 도시의 아프리카계 미국인 비율
• LSTAT : 저소득 계층 비율
• MEDV : 자가 주택의 중간 가격(단위 : 1,000 달러)

데이터에 대한 전반적인 개요를 살펴봤으니, 다음으로 중요 특징을 살펴보자. 탐색적 분석 과정은 머신러닝 모델을 훈련 하기 전에 가장 먼저 수행할 중요하고, 권장하는 단계이기도 하다.
가장 먼저 산점도 행렬을 통해 데이터의 분포 및 특성 간의 상관관계를 파악해보자.

[Python Code]

import matplotlib.pyplot as plt
import seaborn as sns

cols = ['LSTAT', 'INDUS', 'NOX', 'RM', 'MEDV']
sns.pairplot(df[cols], height=2.5)
plt.tight_layout()
save_fig("housing_pairplot")
plt.show()

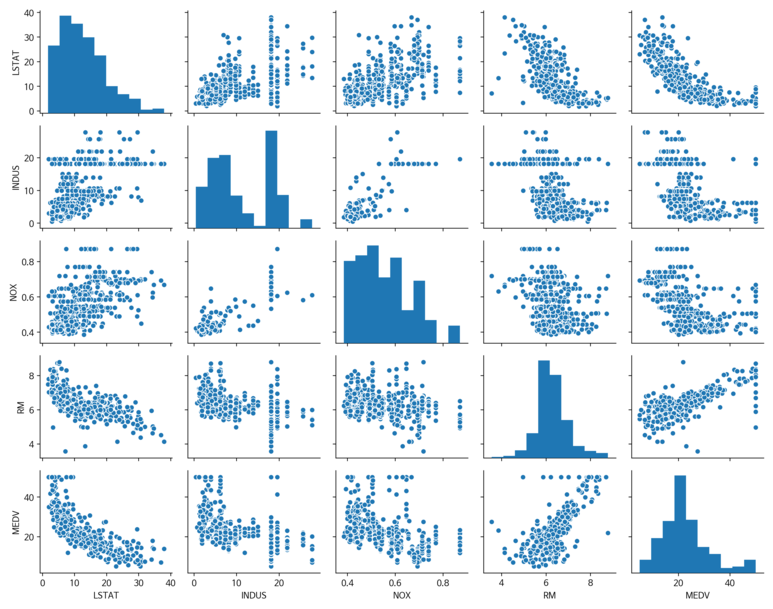
위의 시각화에서 가장 눈에 띄는 것은 RM과 MEDV의 관계이다. 시각화 상으로 두 변수는 서로 양의 선형 관계 있다고 볼 수 있다. 추가적으로 MEDV 데이터 분포가 약간의 이상치가 있지만 정규분포의 형태를 갖는다는 것도 확인할 수 있다. 눈에 명확하게 보여지도록 아래와 같이 히트맵으로 표현해보았다.

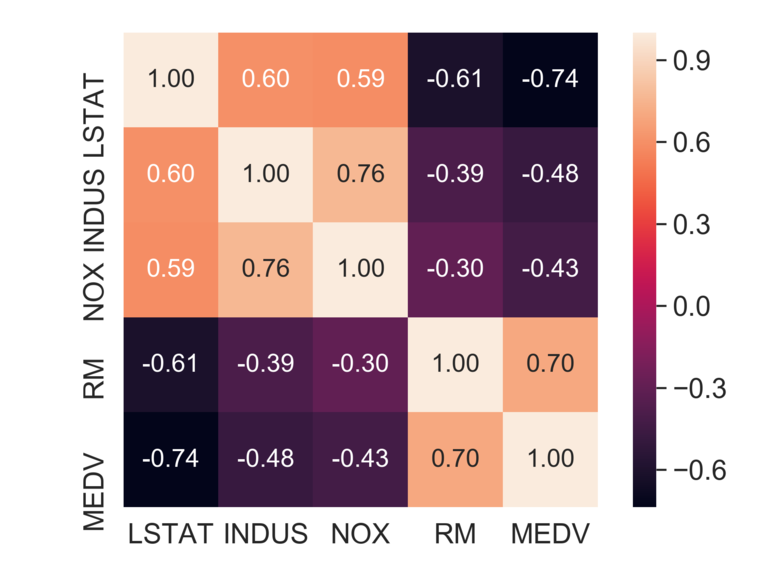
위의 히트맵을 통해서 확인한 결과는 해당 데이터 셋으로 선형회귀 모델을 생성할 경우 설명 변수인 LSTAT와 타깃변수인 MEDV 간의 관계가 제일 높았다. 앞서 살펴본 산점도와 같이 고려해볼 경우 둘 사이에는 확실히 비선형적인 관계였다.
반면, RM과 MEDV 간의 관계 역시 좋은 편이며, 산점도 행렬에서도 서로 선형관계를 갖고 있었기 때문에 RM을 사용하는 것이 제일 좋다고 판단된다.

4) 정규방정식

회귀 모델을 훈련 시킬 때, 먼저 모델이 데이터에 얼마나 잘 들어 맞는 지를 확인해봐야한다. 회귀의 경우 가장 널리 사용되는 것은 성능 측정 지표로, 평균 제곱근 오차(RMSE, Root Mean Squared Error) 를 많이 사용한다.
또한 모델이 최상의 성능을 내도록 하는 값을 확인하기 위해 예측과 훈련 데이터 사이의 거리를 측정하는 비용함수를 정의한다.
정규 방정식은 비용함수를 최소화하는 θ 값을 찾기 위한 해석적인 방법으로 사용하며, 식은 다음과 같다.

$\hat{\theta }\ =\ {\left({X}^T\cdot {X}\right)}^{-1}\cdot {X}^T\cdot y$

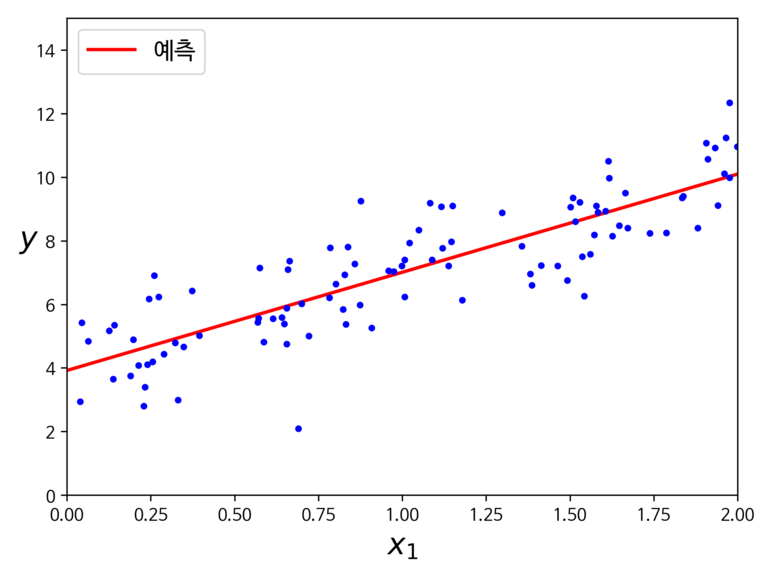
위의 공식을 테스트 하기 위해 아래의 코드를 실행해보자.

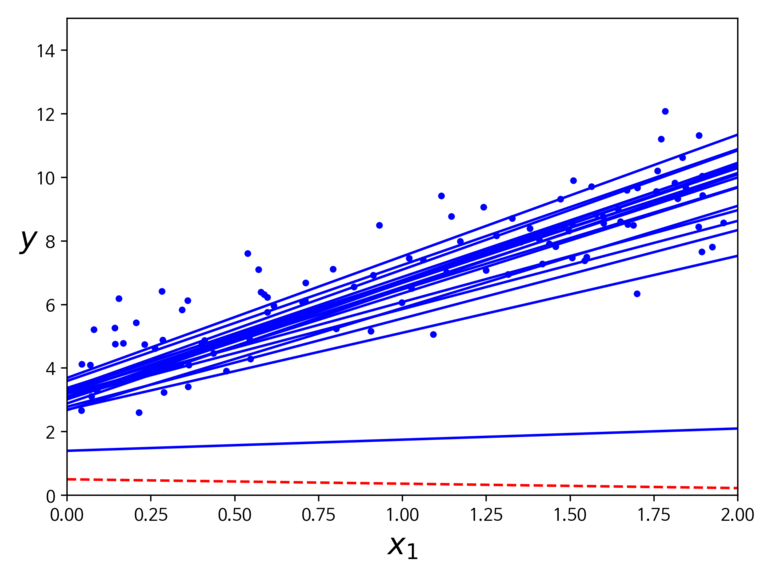
[Python Code]

x = 2 * np.random.rand(100, 1)
y = 4 + 3 * x + np.random.randn(100, 1)

# - dot() : 행렬 곱셈 함수
x_b = np.c_[np.ones((100, 1)), x]
theta_best = np.linalg.inv(x_b.T.dot(x_b)).dot(x_b.T).dot(y)
theta_best

x_new = np.array([[0], [2]])
x_new_b = np.c_[np.ones((2, 1)), x_new]

y_pred = x_new_b.dot(theta_best)
y_pred

plt.plot(x_new, y_pred, "r-", linewidth=2, label="예측")
plt.plot(x, y, "b.")
plt.xlabel("$x_1$", fontsize=18)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.legend(loc="upper left", fontsize=14)
plt.axis([0, 2, 0, 15])
save_fig("linear_model_predictions")
plt.show()

아래의 코드 부분이 정규방정식을 코드로 변형한 부분이다.

[Python Code]

x_b = np.c_[np.ones((100, 1)), x]
theta_best = np.linalg.inv(x_b.T.dot(x_b)).dot(x_b.T).dot(y)

위에서 사용한 코드를 scikit-learn 패키지를 이용해 구현한다면 아래의 코드와 동일하게 동작한다.

[Python Code]

x = 2 * np.random.rand(100, 1)
y = 4 + 3 * x + np.random.randn(100, 1)

lin_reg = LinearRegression()
lin_reg.fit(x, y)
lin_reg.intercept_, lin_reg.coef_

x_new = np.array([[0], [2]])
y_pred_model = lin_reg.predict(x_new)

plt.plot(x_new, y_pred_model, "r-", linewidth=2, label="예측")
plt.plot(x, y, "b.")
plt.xlabel("$x_1$", fontsize=18)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.legend(loc="upper left", fontsize=14)
plt.axis([0, 2, 0, 15])

save_fig("linear_model_predictions_using_lin_reg_func")

plt.show()

2. 경사 하강법

기본 아이디어는 비용 함수를 최소화하기 위해 반복해서 파라미터를 조정해가는 것이다.

1) 경사 하강법의 원리

파라미터 벡터인 θ 에 대해 비용함수의 현재 그래디언트를 계산하고, 그래디언트가 감소하는 방향으로 진행된다.
또한 그래디언트 값이 0이 되면 최솟값에 도달한 것으로 판단한다.좀 더 구체적으로 살펴보자면 θ를 임의의 값으로 시작해 한 번에 조금씩 비용함수가 감소하는 방향으로 진행하여 알고리즘이 최솟값에 수렴할 때까지 점진적으로 향상시킨다.
따라서 중요한 파라미터는 스텝의 크기(반복적 알고리즘 학습에서의 각 단계의 크기)로 학습률(Learning Rate)로 결정된다.
만약 학습률이 너무 낮은 경우 수렴에 도달하기 까지 많은 반복횟수가 존재하므로 시간이 오래걸리며, 너무 큰 경우에는 최솟값을 지나치는 경우가 존재할 수 있다. 아래의 코드를 실행하게 되면 그림과 같이 각 학습률에 대한 선형회귀 결과를 확인할 수 있다.

[Python Code]

# 경사하강법을 이용한 선형 회귀
eta = 0.1               # 학습률
n_iterations = 1000     # 반복횟수
m = 100                 # 샘플 수
theta = np.random.randn(2,1)    # 모델 파라미터

for iteration in range(n_iterations):
    gradients = 2/m * x_b.T.dot(x_b.dot(theta) - y)
    theta = theta - eta * gradients

x_new_b.dot(theta)
theta_path_bgd = []

def plot_gradient_descent(theta, eta, theta_path=None):
    m = len(x_b)
    plt.plot(x, y, "b.")
    n_iterations = 1000

    for iteration in range(n_iterations):
        if iteration < 10:
            y_predict = x_new_b.dot(theta)
        style = "b-" if iteration > 0 else "r--"
    
    plt.plot(x_new, y_predict, style)

    gradients = 2/m * x_b.T.dot(x_b.dot(theta) - y)
    theta = theta - eta * gradients

    if theta_path is not None:
        theta_path.append(theta)

    plt.xlabel("$x_1$", fontsize=18)
    plt.axis([0, 2, 0, 15])
    plt.title(r"$\eta = {}$".format(eta), fontsize=16)

np.random.seed(42)
theta = np.random.randn(2,1)  # random initialization

plt.figure(figsize=(10,4))
plt.subplot(131); plot_gradient_descent(theta, eta=0.02)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.subplot(132); plot_gradient_descent(theta, eta=0.1, theta_path=theta_path_bgd)
plt.subplot(133); plot_gradient_descent(theta, eta=0.5)

save_fig("gradient_descent_plot")

plt.show()

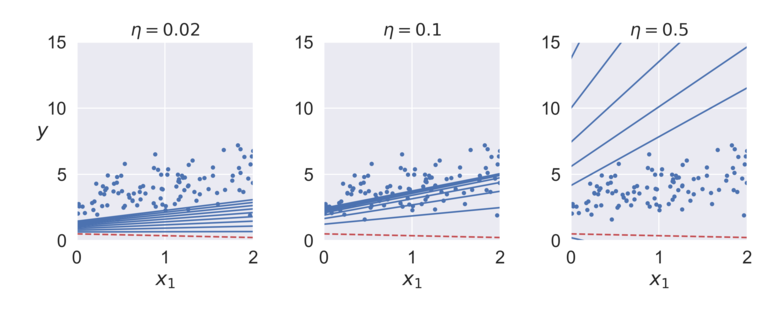
위의 그림을 보면 학습률은 0.1일 때 데이터에 가장 적합하며, 너무 작은 경우에는 데이터의 분포보다 아래에 위치하게되고, 너무 큰 경우에는 데이터 분포 위로 지나쳐버리게 되어 정확도가 낮아지는 것을 볼 수 있다.
선형회귀에서 사용되는 MSE 비용함수는 지역 최솟값이 없고 하나의 전역 최솟값만을 가지는 함수이기 때문에 경사하강법이 전역 최솟값에 가까이 접근할 수 있다.

2) 배치 경사하강법

앞서 언급한 경사하강법을 구현하기 위해서는 각 모델 파라미터인 $\ {θ}_i $ 에 대해 비용함수의 그래디언트를 계산해야 한다. 즉, θi 가 조금 변경될 때 비용함수가 얼마나 바뀌는 가를 계산해야하며, 이를 편도함수 라고 한다. 선형회귀의 경우 아래 식과 같다.

$\frac{\vartheta }{\vartheta {\theta }_i}\ MSE\left(\theta \right)\ =\ \frac{2}{m}\sum _{i=1}^m\left({\theta }^T\cdot {X}^{\left(i\right)}\ -{Y}^{\left(i\right)}\ \right)\ {X}_j^{\left(i\right)}$

반복 횟수의 경우에는 아주 크게 지정하고, 대신 그래디언트 벡터를 아주 작게 지정하게 되면, 벡터의 노름이 임의 값 ε 보다 작아지게 되는 시점이 최솟값에 도달한 것과 일치하여 알고리즘이 중지하게 된다.
이를 앞서 실습한 주택 데이터에 경사하강법을 적용해보자. 코드는 아래와 같다.

[Python Code]

class LinearRegressionGD(object):
    def __init__(self, eta=0.001, n_iter=20):
        self.eta = eta
        self.n_iter = n_iter

    def fit(self, x, y):
        self.w_ = np.zeros(1 + x.shape[1])
        self.cost_ = []

        for i in range(self.n_iter):
            output = self.net_input(x)
            errors = (y-output)
            self.w_[1:] += self.eta * x.T.dot(errors)
            self.w_[0] += self.eta * errors.sum()
            cost = (errors**2).sum() / 2.0
            self.cost_.append(cost)

        return self

    def net_input(self, x):
        return np.dot(x, self.w_[1:]) + self.w_[0]

    def predict(self, x):
        return self.net_input(x)

x = df[['RM']].values
y = df['MEDV'].values

sc_x = StandardScaler()
sc_y = StandardScaler()

x_std = sc_x.fit_transform(x)
y_std = sc_y.fit_transform(y[:, np.newaxis]).flatten()

model = LinearRegressionGD()
model.fit(x_std, y_std)

plt.plot(range(1, model.n_iter+1), model.cost_)
plt.ylabel("SSE")
plt.xlabel("Epoch")
save_fig("housing_gradient_descent")
plt.show()

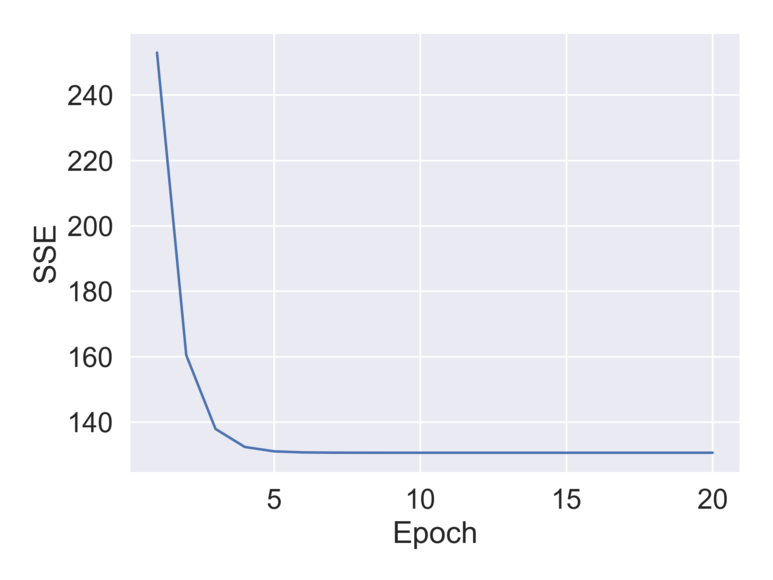
앞선 실습에서 RM과 MEDV 간의 관계가 제일 선형적이라고 하였다. 하지만 값의 분포가 다르기 때문에 StandardScaler() 를 이용해 표준화를 시켜 분포를 동일하게 맞춰준 다음, 경사하강법을 적용하였다.
사이킷런에 존재하는 대부분의 변환기는 데이터가 2차원 배열 형식이기 때문에 np.newaxis() 를 이용해 배열에 새로운 차원을 추가 함으로써 2차원 배열 형식을 맞춰준다. 이 후 StandardScaler()로 조정된 결과가 반환되면 flatten() 메소드를 통해 본래의 1차원 배열 형태로 돌려준다.

경사하강법과 같이 최적화 알고리즘을 다룰 때는 훈련 데이터 셋에 대한 비용을 위의 시각화처럼 그려보는 편이 좋다. 위의 시각화에서는 비용함수의 최솟값으로 수렴하는 것을 확인할 수 있었다. 다음으로 회귀 직선과 잔차를 확인해보자. 이를 위해 아래의 코드를 실행한다.

[Python Code]

def lin_regplot(x, y, model):
    plt.scatter(x, y, c="steelblue", edgecolors="white", s=60)
    plt.plot(x, model.predict(x), color="red", lw=2)
    
    return None

lin_regplot(x_std, y_std, model)

plt.xlabel("평균 방 갯수(RM)")
plt.ylabel("가격(MEDV)")

save_fig("housing_lin_regplot")

plt.show()

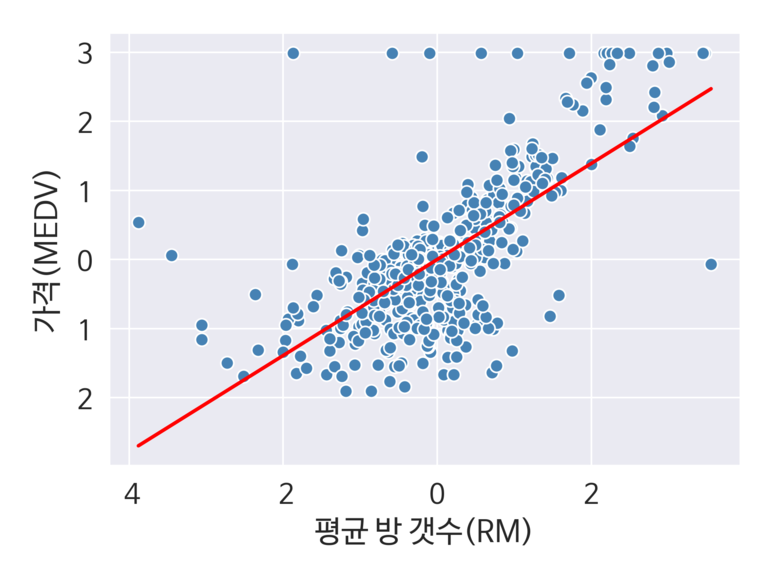
위의 시각화를 통해 방의 갯수가 많을 수록 가격이 상승한다는 관계를 볼 수 있다.
매우 직관적으로 보여지는 부분이며, 방의 갯수와 주택가격으로는 해당 데이터를 잘 설명하지 못한다는 점을 볼 수 있다.

3) 확률적 경사 하강법

매 스텝에서 딱 한 개의 샘플을 무작위로 선택하고 하나의 샘플에 대한 그래디언트를 계산한다. 매우 적은 데이터만을 처리하기 때문에 알고리즘이 훨씬 빠르지만, 확률적이기 때문에 비용함수가 최솟값에 도달할 때까지 부드럽게 감소하지 않고 위아래로 요동치면서 평균적으로 감소하는 경향을 보일 수 있다. 그럼에도 배치 경사 하강법 보다는 전역 최솟값을 찾을 가능성이 높기 때문에 많이 이용된다.
이를 보고 금속공학분야에서 가열한 금속을 천천히 냉각 시키는 어닐링 과정이라고 하기도 한다. 또한 매 반복에서 학습률을 결정하는 함수를 학습 스케줄 이라고 한다. 이를 너무 빨리 줄어들게 하면 지역 최솟값에 갇히거나 중간에 멈출 수 있다. 반면, 너무 천천히 줄어들면 오랫동안 최솟값 주변을 맴돌거나 지역 최솟값에 머무를 수 있다.

[Python Code]

n_epochs = 50
t0, t1 = 5, 50

theta_path_sgd = []
m = len(x_b)
np.random.seed(42)

def learning_schedule(t):
    return t0 / (t + t1)

theta = np.random.randn(2, 1)

for epoch in range(n_epochs):
    for i in range(m):
        if epoch == 0 and i < 20:
            y_predict = x_new_b.dot(theta)
            style = "b-" if i > 0 else "r--"
            plt.plot(x_new, y_predict, style)
            
        random_index = np.random.randint(m)
        
        xi = x_b[random_index:random_index+1]
        yi = y[random_index:random_index+1]

        gradients = 2 * xi.T.dot(xi.dot(theta) - yi)
        eta = learning_schedule(epoch * m + i)
        theta = theta - eta * gradients

        theta_path_sgd.append(theta)

plt.plot(x, y, "b.")
plt.xlabel("$x_1$", fontsize=18)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.axis([0, 2, 0, 15])

save_fig("sgd_plot")

plt.show()

샘플을 무작위로 선택하기 때문에 한 샘플이 여러 번 반복될 수도 있고 어떤 샘플은 선택받지 못하고 학습이 끝나는 경우도 있다. 사이킷 런에서는 SGD 방식으로 선형 회귀를 사용하려면 기본 값으로 제곱 오차 피용함수를 최적화 하는 SGDRegressor 클래스를 사용한다.

[Python Code]

sgd_reg = SGDRegressor(max_iter=5, penalty=None, eta0=0.1, random_state=42)
sgd_reg.fit(x, y.ravel())
sgd_reg.intercept_, sgd_reg.coef_

4) 미니배치 경사 하강법

각 스텝에서 미니 배치라 부르는 임의의 작은 샘플 세트에 대해 그래디언트를 계산한다. 주요 장점은 행렬 연산에 최적화된 하드웨어(GPU)를 사용해서 얻는 성능 향상이다. 미니배치를 어느정도 크게 하면 파라미터 공간에서 SGD 보다 덜 불규칙적으로 움직인다. 결과적으로 SGD보다는 최솟값에 더 근접할 수 있지만 지역 최솟값을 빠져나오는 것은 SGD 보다 어려울 수 있다.
아래의 그림은 지금까지 살펴본 3가지 경사 하강법 알고리즘이 훈련 과정 동안 파라미터 공간에서 움직인 경로를 보여준다.

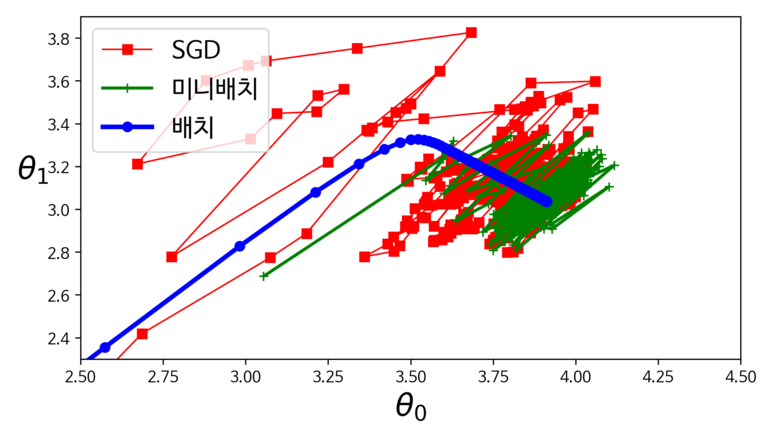
결과적으로 모두 최솟값에 도달하였으나 배치 경사 하강법의 경로가 실제로 최솟값에서 멈춘 데 반해. 확률적 경사하강법(SGD)와 미니배치의 경우 최솟값 근처에서 맴도는 현상을 볼 수 있다.
위의 결과를 통해 확률적 경사하강법과 미니배치 경사하강법을 이용할 때는 반드시 학습 스케줄을 사용하면 최솟 값에 도달한다는 내용을 한 번더 확인할 수 있다.

3. 회귀 모델의 가중치 추정

앞선 2개의 실습을 통해 회귀분석을 위한 모델을 생성하였다. 하지만 실전에서는 좀 더 빠른 시간내에 효율적인 모델을 구현하는 것이 좋다. 이럴 경우 scikit-learn에서는 LIBLINEAR 라이브러리와 고수준 최적화 알고리즘을 사용한다. 추가적으로 필요하나 표준화되지 않은 변수를 사용할 때에 잘 동작하기 위해서 최적화 기법을 사용한다.
앞서 실습한 주택 가격을 예시로 가중치 추정을 적용해보자면 아래 코드처럼 할 수 있다.

[Python Code]

x = df[['RM']].values
y = df['MEDV'].values

slr = LinearRegression()
slr.fit(x, y)
print("기울기 : %.3f" % slr.coef_[0])
print("절편 : %.3f" % slr.intercept_)

lin_regplot(x, y, slr)

plt.xlabel("방 갯수(RM)")
plt.ylabel("가격($1000 단위) (MEDV)")
save_fig("linear_weight_prediction")
plt.show()

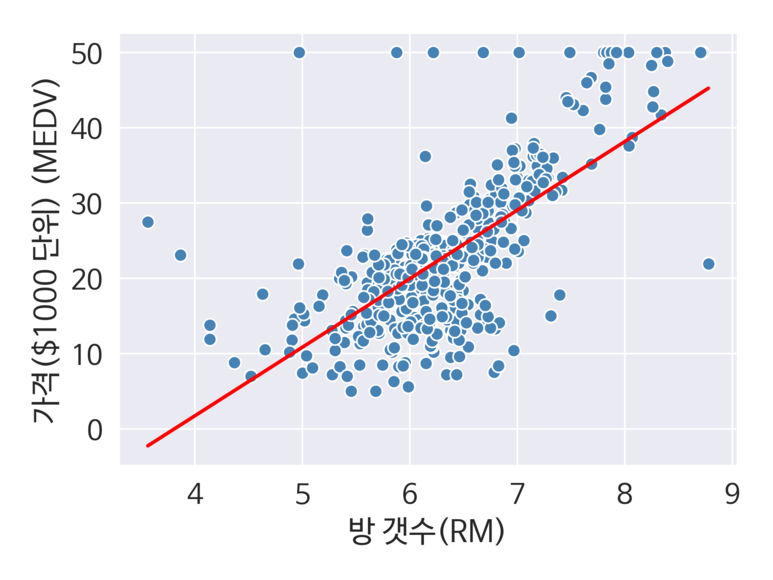
4. RANSAC을 이용한 안정된 회귀 모델 훈련

회귀 모델의 단점 중 하나는 이상치에 매우 크게 영향을 받는다는 점이다. 아주 작은 부분이더라도 추정모델의 가중치에 크게 영향을 주기 때문이다. 따라서 이상치를 제거하는 방식 혹은 안정된 모델을 사용하는 것이 모델 성능에 좋을 것이다. RANSAC은 안정적인 회귀 모델로 정상치라는 일부 데이터를 이용해 훈련을 하며, 과정은 아래의 내용과 같다.

1) RANSAC 훈련과정

① 랜덤하게 일부 샘플을 정상치로 선택해 모델을 훈련한다.
② 훈련된 모델에서 다른 모든 포인트를 테스트한다.
    → 입력한 허용오차안에 속한 포인트를 정상치에 추가한다.
③ 모든 정상치를 사용하여 모델을 다시 훈련한다.
④ 훈련된 모델과 정상치 간의 오차를 추정한다.
⑤ 성능이 사용자가 지정한 임계값에 도달하거나 지정된 반복횟수에 도달하면 알고리즘을 종료한다. 아닐 경우 ① 로 돌아간다.

scikit-learn 에서 정상치의 임계값의 기본 값은 MAD 추정이다. 이는 타깃 값 y의 중앙값 절대 편차를 의미한다.
하지만 적절한 정상치 임계값은 문제에 따라 다르기 때문에 RANSAC 알고리즘의 단점이 된다. 아래의 코드를 통해 주택 가격 데이터에 RANSAC 모델을 적용해보자.

[Python Code]

# 실습 4. RANSAC 회귀
ransac = RANSACRegressor(LinearRegression(), max_trials=100, min_samples=50, loss='absolute_loss', residual_threshold=5.0, random_state=0)
ransac.fit(x,y)
inlier_mask = ransac.inlier_mask_
outlier_mask = np.logical_not(inlier_mask)
line_x = np.arange(3, 10, 1)
line_y = ransac.predict(line_x[:, np.newaxis])

plt.scatter(x[inlier_mask], y[inlier_mask], c='steelblue', edgecolors='white', marker='o', label='Inliers')
plt.scatter(x[outlier_mask], y[outlier_mask], c='limegreen', edgecolors='white', marker='s', label='Outliers')
plt.plot(line_x, line_y, color='black', lw=2)
plt.xlabel('평균 방 갯수(RM)')
plt.ylabel('가격(MEDV)')
plt.legend(loc='upper left')
save_fig("ransac_linear_regression")
plt.show()

[실행결과]

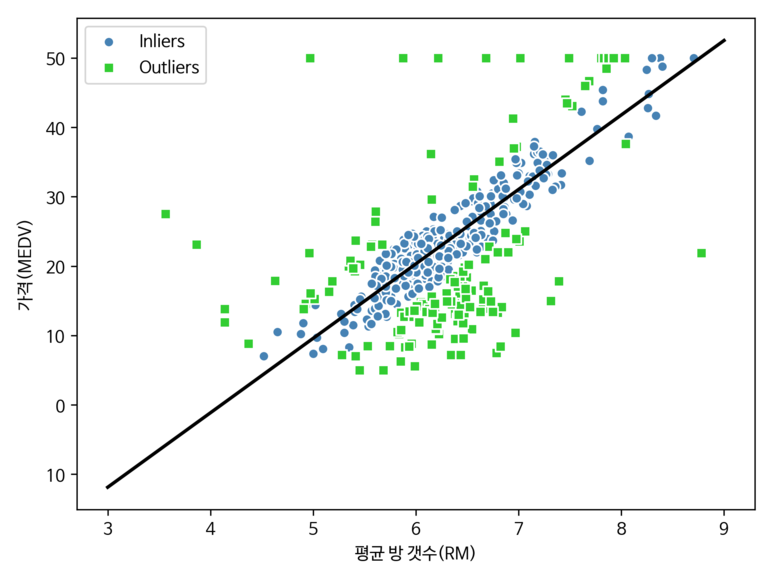
또한 아래의 코드를 사용해보면 이전에 구현한 선형회귀의 기울기와 다른 것을 확인할 수 있다.

[Python Code]

print('기울기 : , %.3f' % ransac.estimator_.coef_[0])
print('절편 : %.3f' % ransac.estimator_.intercept_)

[실행결과]

기울기 : , 10.735
절편 : -44.089

이처럼 RANSAC을 사용하면 데이터 셋에 있는 이상치의 잠재적인 영향을 감소시킨다. 하지만 본 적 없는 데이터에 대한 예측 성능에 긍정적인 영향을 미치는지 알지 못한다.

5. 선형회귀 성능 평가

회귀 모델에 대한 성능을 조사할 땐 크게 잔차 분석과 평균제곱오차 계산 방법이 있다.

1) 잔차 분석

잔차 분석은 회귀 모델을 진단할 때 자주 사용되며, 잔차 그래프를 통해 실제 값과 예측값 사이의 차이(혹은 수직거리)를 알 수 있다. 이는 비선형성과 이상치를 감지하고 오차가 랜덤하게 분포되어 있는지를 확인할 때 도움이 된다. 아래 코드를 통해 잔차 그래프를 그려보자.

[Python Code]

# 성능평가
x = df.iloc[:, :-1].values
y = df['MEDV'].values

x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3, random_state=0)

slr = LinearRegression()
slr.fit(x_train, y_train)

y_train_pred = slr.predict(x_train)
y_test_pred = slr.predict(x_test)

plt.scatter(y_train_pred, y_train_pred - y_train, c='steelblue', marker='o', edgecolors='white', label='Training Data')
plt.scatter(y_test_pred, y_test_pred - y_test, c='limegreen', marker='s', edgecolors='white', label='Test Data')

plt.xlabel("Predicted Values")
plt.ylabel("Residual")

plt.legend(loc="upper left")
plt.hlines(y=0, xmin=-10, xmax=50, color='black', lw=2)
plt.xlim([-10,50])
plt.tight_layout()

save_fig("Residual Graph")

plt.show()

[실행 결과]

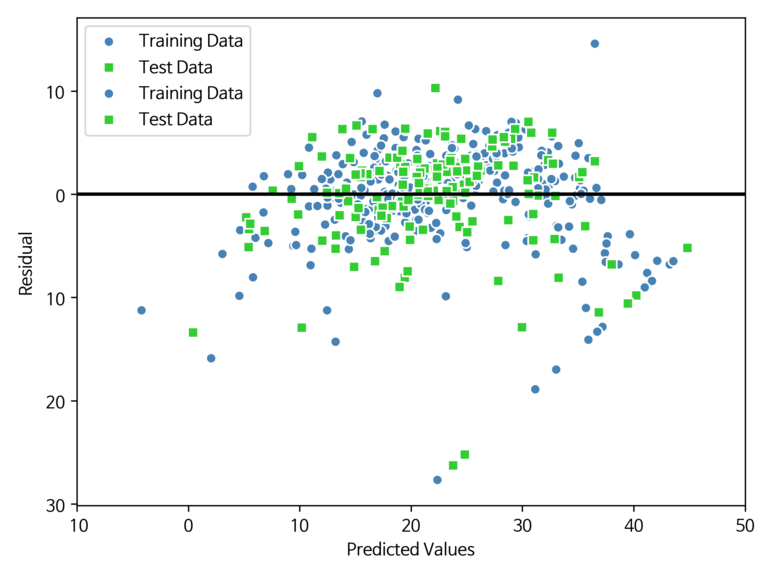
예측이 완벽하다면 잔차는 0이 된다. 하지만 현실에서는 절대 일어나지 않는 현상이며, 대신 좋은 회귀 모델이라면 오차가 랜덤하게 분포하고, 잔차는 중앙선 주변으로 랜덤하게 흩어지는 현상이 보여야한다.
만약 잔차 그래프에서 패턴이 나타나면 특성에서 어떤 정보를 잡아내지 못하고 잔차로 새어 나갔다고 한다.
잔차 분석은 주로 이상치의 유·무를 확인할 때 사용되며, 확인 방법은 중앙선에서 큰 편차를 낸 포인트들이 해당된다.

2) 평균 제곱 오차와 결정 계수

두번째 방법은 평균 제곱 오차를 확인하는 방법이다. 선형 회귀 모델을 훈련하기 위해서 최소화하는 제곱 오차 항의 평균을 의미한다. 주로 그리드 서치와 교차 검증에서 매개변수를 튜닝하거나 다른 회귀 모델을 비교할 때 유용하다. 식은 다음과 같다.

$MSE\ =\ \frac{1}{n}\sum _{i=1}^n{\left({y}^{\left(i\right)}-{\hat{y}}^{\left(i\right)}\right)}^2$

다음으로 앞서 실습한 주택 가격 데이터를 이용해 훈련 세트와 테스트 세트의 예측에 대한 MSE를 계산해보자.

[Python Code]

## 평균제곱오차(MSE)
print("훈련 MSE : %.3f, 테스트 MSE: %.3f" % (mean_squared_error(y_train, y_train_pred), mean_squared_error(y_test, y_test_pred)))

[실행 결과]

훈련 MSE : 19.958, 테스트 MSE: 27.196

평균제곱 오차 대신 결정계수를 이용할 수 있다. 결정 계수는 모델 성능을 잘 해석하기 위해 만든 MSE의 표준화된 버전이다. 계산식은 다음과 같다.

${R}^2\ =\ 1-\frac{SSE}{SST}$

위 수식에서 SSE는 제곱 오차항을 의미하고, SST는 전체 제곱합을 의미한다. SST를 계산하는 방법은 아래와 같다.

$SST\ =\ \sum _{i=1}^n{\left({y}^{\left(i\right)}-{\mu }_y\right)}^2$

결과적으로 SST는 단순히 타겟의 분산을 의미하는 것과 같다. 다음으로 결정계수가 MSE의 표준화된 버전이 맞는지도 살펴보자. 증명은 아래와 같다.

${R}^2\ =1-\frac{SSE}{SST}$
$\ \ \ \ \ =1-\frac{\frac{1}{n}\sum_{i=1}^n{\left({y}^{\left(i\right)}-{\hat{y}}^{\left(i\right)}\right)}^2}{\frac{1}{n}\sum _{i=1}^n{\left({y}^{\left(i\right)}\ -{\mu }_y\right)}^2}$
$\ \ \ \ \ =1-\frac{MSE}{Var\left(y\right)}$

훈련 세트에 대해 R2 은 0~1사이의 값을 가진다. 실제로 아래코드를 이용해 주택 가격 데이터에 대한 결정계수를 계산해보자.

[Python Code]

## 결정 계수
print("훈련 R^2: %.3f, 테스트 R^2: %.3f" % (r2_score(y_train, y_train_pred), r2_score(y_test, y_test_pred)))

[실행 결과]

훈련 R^2: 0.765, 테스트 R^2: 0.673

6. 규제 (Penalized Regression)

회귀 모델에서 규제란 부가정보를 손실에 더해 과대적합 문제를 방지하는 방법이며, 복잡도에 대한 페널티를 유도해 모델 파라미터의 값을 감소시킨다. OLS(Ordinary Least Squares, 최소 제곱 회귀) 라고 불리는 최소 제곱 회귀방법의 일종이며, 과적합과 부적합 사이의 균형 조정 파라미터로 볼 수 있다. 주로 유전 정보나 텍스트 마이닝 같은 입력 파라미터가 너무 많은 문제에 적용되며, 가장 많이 이용되는 방법은 릿지 회귀, 라쏘 회귀, 엘라스틱 넷이 있다. 장점으로는 다음과 같은 항목을 들 수 있다.

• 모델 트레이닝 속도가 극단적으로 빠르다.
• 변수 중요도 정보를 제공한다
• 평가가 극단적으로 빠르다
• 다양한 문제에서 높은 성능을 보인다.
• 선형 모형이 꼭 필요한 경우가 있다.

1) Ridge 회귀(Ridge Regression)

Ridge 회귀는 단순히 최소 제곱 비용 함수에 가중치의 제곱합을 추가한 L2 규제 모델이다. 비용함수는 다음과 같다.

Ridge 회귀는 단순히 최소 제곱 비용 함수에 가중치의 제곱합을 추가한 L2 규제 모델이다. 비용함수는 다음과 같다.

$ {J\left(w\right)}_{RIDGE}= \sum _{i=1}^n{({y}^{(i)}-{\hat{y}}^{(i)})}^2 + \lambda {\Vert{w}\Vert}_2^2 $

위의 수식에서 $ \lambda {\Vert{w}\Vert}_2^2 $ 부분이 규제항(가중치 벡터의 L2 노름)이며 전개해보면 다음과 같다.

$ L2 = \lambda {\Vert{w}\Vert}_2^2 = \lambda \sum _{j=1}^m{w}_j^2 $

하이퍼 파라미터 λ 를 증가시키면 규제 강도가 증가되고 모델의 가중치 값이 감소한다. 만약 λ = 0 일 경우, Ridge 회귀는 선형회귀와 동일하게 된다. 반면 가중치가 아주 큰 경우 모든 가중치가 거의 0에 가까워지고 결국 데이터의 평균을 지나는 수평선이 된다.
Ridge 회귀 비용함수에서 절편에 해당하는 w0 는 규제하지 않는다. 모델의 복잡도와 절편은 관계가 없기 때문이다. 만약 경사하강법에 적용하려면 MSE 그레디언트 벡터에 λw 를 더하면 된다. 아래의 그림을 통해 좀 더 살펴보자.

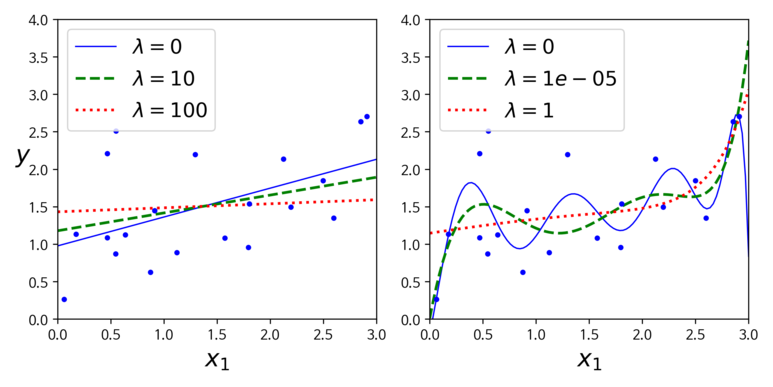
아래의 그래프를 살펴보면 λ 를 증가 시킬 수록 직선에 가까워지는 것을 볼 수 있다.반면 값을 줄이게 되면 모델의 분산은 줄지만 편향이 커지는 현상을 볼 수 있다. 선형 회귀와 마찬가지로 정규방정식을 사용할 수도 있고, 경사하강법을 적용할 수도 있다. 각각의 경우는 아래의 코드로 구현할 수 있다.

[Python code]

# 정규방정식을 적용한 Ridge 회귀
ridge_reg = Ridge(alpha=1, solver="cholesky", random_state=42)
ridge_reg.fit(x, y)
ridge_reg.predict([[1.5]])

# 확률적 경사하강법을 적용한 Ridge 회귀
sgd_reg = SGDRegressor(max_iter=50, penalty="l2", tol=1e-3, random_state=42)
sgd_reg.fit(x, y.ravel())
sgd_reg.predict([[1.5]])

확률적 경사하강법을 적용한 경우 penalty 매개변수에는 “l2” 를 명시해줘야하며, 이는 SGD가 비용함수에 가중치 벡터의 L2 노름의 제곱을 2로 나눈 규제항을 추가하게 한다.

2) LASSO 회귀

LASSO 회귀는 Ridge 회귀 처럼 비용 함수에 규제항을 더하지만 L2 노름의 제곱을 2로 나눈 것 대신 가중치 벡터의 L1 노름을 사용한다. 규제 강도에 따라서 어떤 가중치는 0이 될 수 있다. 비용함수는 다음과 같다.

$ {J\left(w\right)}_{LASSO}= \sum _{i=1}^n{({y}^{(i)}-{\hat{y}}^{(i)})}^2 + \lambda {\Vert{w}\Vert}_1 $

사용된 규제항의 식을 전개하면 아래와 같다.

$ L1 = \lambda {\Vert{w}\Vert}_1 = \lambda \sum _{j=1}^m{\vert{w}_j\vert} $

위의 두 식에 대해 만약 m > n 인 상황이라면 최대 n개의 특성을 선택하는 것이 LASSO 회귀의 한계이다. LASSO 회귀에서의 중요한 특징이 덜 중요한 특성의 가중치를 완전히 제거하려고 하는 것이기 때문이다. 아래 그래프를 통해 좀 더 살펴보자.

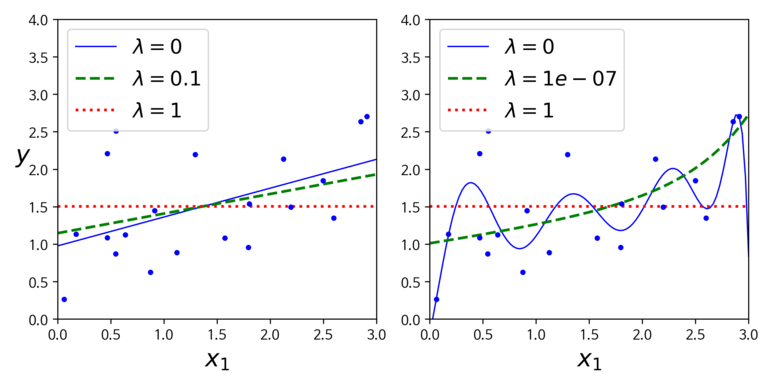
위의 그래프에서 볼 수 있듯이 오른쪽 그래프의 λ=1e-07 인 경우에 2차방정식처럼 보이며 선형적인 현상을 볼 수 있다. 다시 말해 자동으로 특성 선택을 하고 희소 모델을 만든다고 할 수 있다. 추가적인 예시로 다음 그림을 한번 살펴보자.

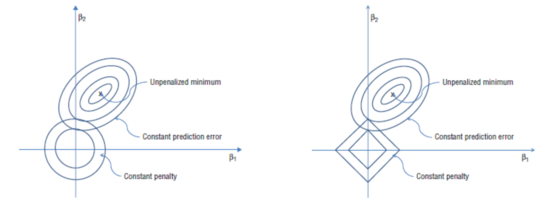
위의 그림은 Ridge회귀와 LASSO 회귀를 오차에 적용했을 때의 모습을 보여준다. 우선 왼쪽이 Ridge, 오른쪽이 LASSO 회귀라는 점을 알아두자. 각 그래프에서 중앙에 위치한 원 혹은 마름모 꼴은 페널티를 의미한다. 또한 그래프 우측 상단에 위치한 타원형은 x,y 의 변화량을 β1, β2 라고 할 경우 (β1,β2) 일 때의 자료에 대한 오차집합체라고 할 수 있다. 일반적으로 LASSO의 경우 접점에서 만나기 때문에 자료가 넓게 퍼져있는 것을 선호하며, Ridge의 경우 축 위에서 만나기 때문에 가로축의 값이 0이 되는 것을 선호하는 경향을 보인다.
Ridge의 경우, 만약 동심원이 0이 된다(점이 되는 것)이며 타원형이 갖는 오차 범위가 넓어진다. 타원의 중심이면 최적의 값이자 동심원의 최대 크기지만 학습 자료의 데이터이기 때문에 정확한 값은 아니다.(집합체 안의 일부 값들은 스케일 상 너무 큰 값이 있어서 실제사례로는 적합하지않다.) 따라서 두 원의 접점에 있을 때가 더 적합하다.
LASSO의 경우 자료오차 차원이 각 축의 점에 걸린다. 즉, 어느 하나만 크게 하고 나머지는 0으로 준다.

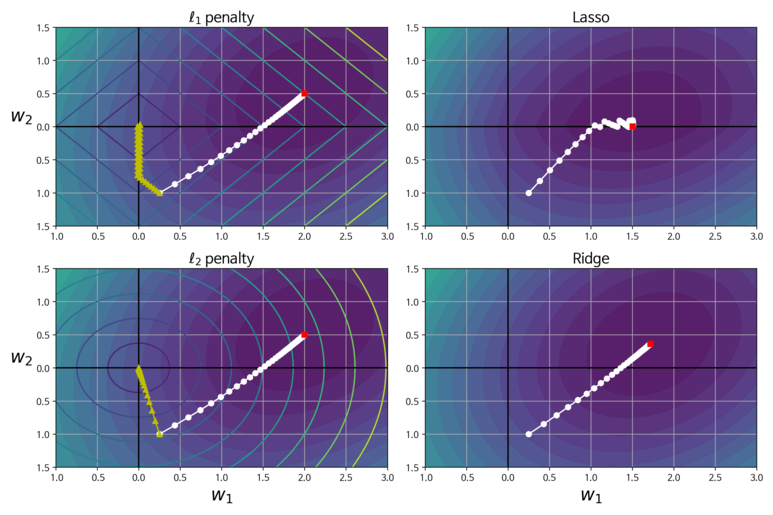
이 그림은 각 회귀모델을 배치 경사하강법을 이용해 그래디언트가 이동하는 경로를 표시한 것이다.
왼쪽 위의 그래프 내 배경의 원형 등고선이 규제가 없는 MSE 함수를 의미한다. 마름모 꼴의 등고선은 L1 페널티를 나타내며, 노란색 삼각형은 페널티에 대한 배치 경사 하강법의 경로이다. 경로는 먼저 W1 =0 에 도달하고 나서 w2 = 0에 다다를 때 까지 좌표축을 따라 내려간다.
오른쪽 위의 그래프에서 등고선이 나타내는 것은 λ = 0.5의 L1 페널티가 더해진 비용함수를 나타낸 것이다. 전역변수 최소값은 w2 축에 있으며, w2 에 도달하고 난 후 전역 최솟값에 도달할 때까지 좁은 경로를 따라 이동하고 있다. 추가적으로 경사 하강법의 경로가 종착지에 근접할 수록 지그재그로 튀는 현상을 볼 수 있는데, 전역 최소값에 수렴하기 위해 학습률을 점진적으로 줄이는 과정에서 갑자기 기울기가 변하기 때문이다. 하단의 2개 그래프 역시 L2 페널티를 이용한 것 외에 동일한 조건이다. 가중치가 완전히 제거 되지 않았지만, 최저값이 규제가 없는 경우 보다 w=0에 더 근접했다.

3) ElasticNet

Ridge 회귀와 LASSO 회귀의 절충안이라고 할 수 있다. 희소한 모델을 만들기 위한 L1 페널티와 선택 특성 개수가 같은 LASSO의 한계를 극복하기 위한 L2 페널티를 가진다. 비용함수는 아래와 같다.

$J(w)_{ElasticNet}=\sum _{i=1}^n({y}^{(i)} - {\hat{y}}^{(i)})^2 + r{\lambda}_1\sum _{j=1}^m{w}_j^2 + \frac {1-r}{2} {\lambda }_2 \sum _{j=1}^m\vert{w}_j\vert $

규제항은 Ridge와 LASSO 회귀의 규제항을 단순히 더해서 사용하며 혼합비율 r 을 이용해 조절한다. r = 0 이면 엘라스틱넷은 Ridge 회귀와 같고, r = 1 이면 LASSO 회귀와 같다. 규제가 작게라도 있는 것이 좋기 때문에 일반적으로 평범한 선형회귀는 피해야한다.
또한 실제로 사용되는 특성이 몇 개뿐인 경우라면, LASSO 나 ElasticNet을 사용하는 것이 좋다. 그리고 특성 수가 훈련 샘플의 수보다 많거나, 특성 몇 개가 가아게 연관되어 있는 경우 LASSO 보다는 ElasticNet을 사용하는 편이 좋다.

7. 다항 회귀

다항 회귀는 각 특성의 거듭 제곱으로 새로운 특성을 추가하고 확장된 특성을 포함한 데이터 셋에 선형 모델을 훈련 시키는 것이다. 선형 가정이 어긋날 때 대처 방법으로 활용할 수 있으며, 모델에 대한 함수는 다음과 같다.

$y={w}_0+{w}_1x+{w}_2{x}^2+…+{w}_n{x}^n$

여기서 n 은 다항식의 차수를 의미한다. 다항 회귀를 사용해 비선형 관계를 모델링하는 경우가 있지만 선형 회귀 가중치인 w 때문에 다변량 선형회귀모델로 생각할 수 있다. 예를 들어 아래와 같은 분포의 데이터가 존재한다고 가정해보자.

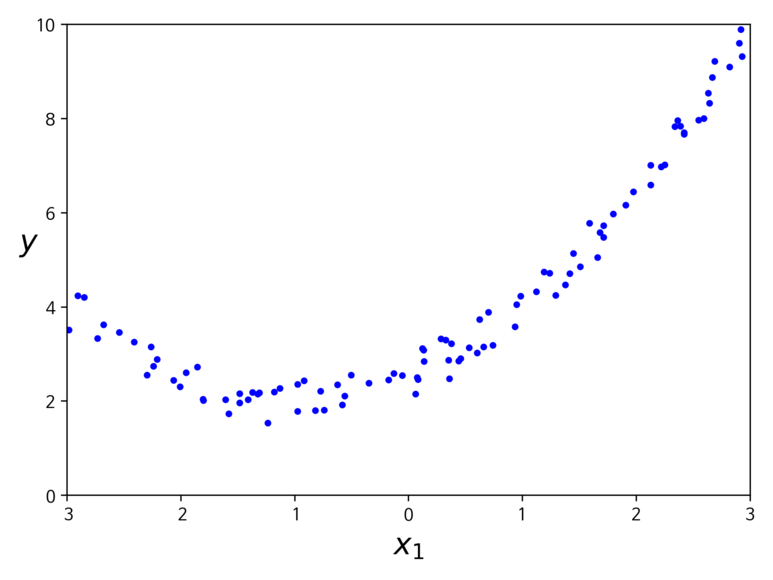
위와 같은 데이터라면 단순히 직선형 회귀 모델로는 적합하지 않을 것이다. 따라서 scikit-learn의 PolynomialFetures를 사용해 훈련 데이터를 변환해보자.

[Python Code]

from sklearn.preprocessing import PolynomialFeatures
...

poly_features = PolynomialFeatures(degree=2, include_bias=False)
x_poly = poly_features.fit_transform(x)

x[0]
x_poly[0]

[실행 결과]

Out[9]: array([-1.12973354])
Out[10]: array([-1.12973354,  1.27629788])

이제 확장된 훈련 데이터에 적용하게 되면 다음과 같은 결과를 얻을 수 있다.

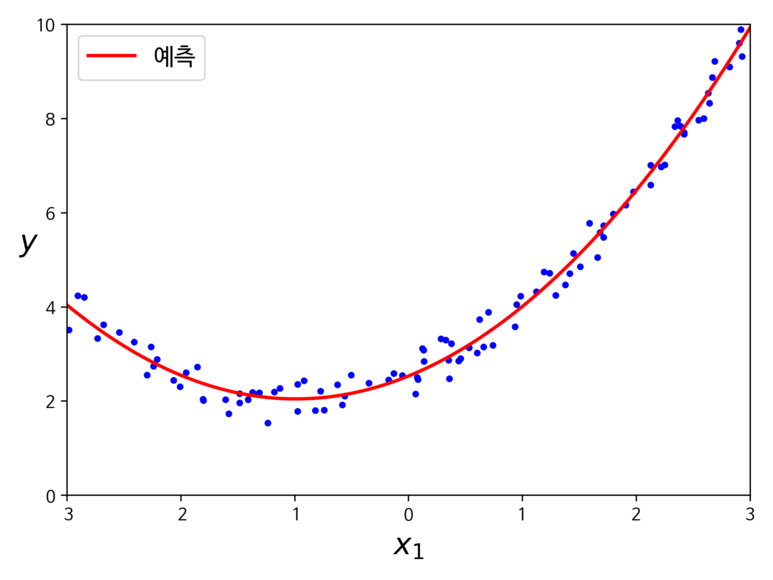
이번에는 앞서 실습한 주택 가격 데이터에 다항 회귀를 적용해서 비선형 관계 모델링을 진행해보자.

[Python Code]

x = df[['LSTAT']].values
y = df[['MEDV']].values

model = LinearRegression()

quadratic = PolynomialFeatures(degree=2)
cubic = PolynomialFeatures(degree=3)
x_quad = quadratic.fit_transform(x)
x_cubic = cubic.fit_transform(x)

x_fit = np.arange(x.min(), x.max(), 1)[:, np.newaxis]
model = model.fit(x, y)
y_fit = model.predict(x_fit)
r2 = r2_score(y, model.predict(x))

model = model.fit(x_quad,y)
y_quad_fit = model.predict(quadratic.fit_transform(x_fit))
quadratic_r2 = r2_score(y, model.predict(x_quad))

model = model.fit(x_cubic,y)
y_cubic_fit = model.predict(cubic.fit_transform(x_fit))
cubic_r2 = r2_score(y, model.predict(x_cubic))

plt.scatter(x, y, label="Training Point", color="lightgray")
plt.plot(x_fit, y_fit, label="linear (d=1), $R^2=%.2f$" % r2, color="blue", lw=2, linestyle=":")
plt.plot(x_fit, y_quad_fit, label="quadratic (d=2), $R^2=%.2f$" % quadratic_r2, color="red", lw=2, linestyle="-")
plt.plot(x_fit, y_cubic_fit, label="cubic (d=3), $R^2=%.2f$" % cubic_r2, color="green", lw=2, linestyle="--")
plt.xlabel("% lower status of the popualtion[LSTAT]")
plt.ylabel("Price of $1000 [MEDV]")
plt.legend(loc="upper right")

save_fig("Multi Regression")

plt.show()

[실행 결과]

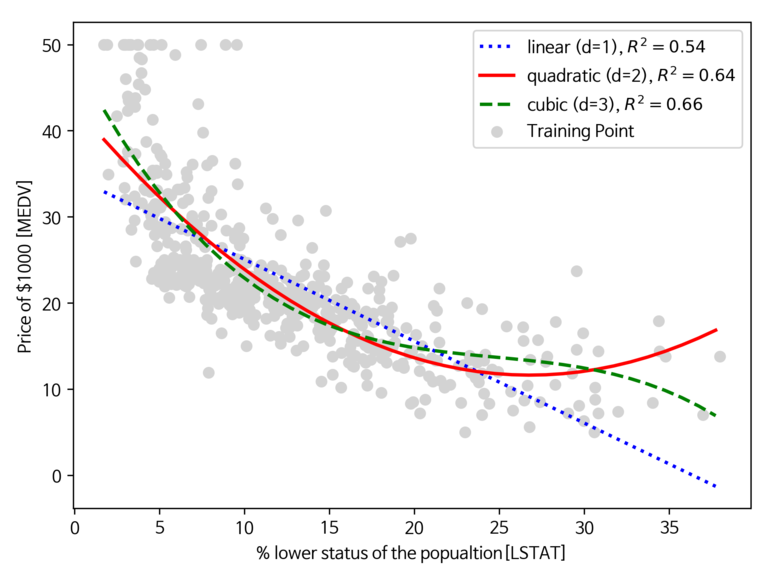
위의 그림을 통해 알 수 있듯이, 선형과 2차 다항 모델 보다 3차 다항모델이 주택가격과 LSTAT 사이의 관계를 잘 잡아낸다. 하지만 다항 특성이 많이 추가될 수록 모델 복잡도가 높아지고 과대적합의 가능성이 증가할 수 있다. 따라서 만일 실전에서 사용하는 경우 별도의 테스트 세트에서 모델의 일반화 성능을 평가하는 것을 권장한다.

8. 로지스틱 회귀

샘플이 특정 클래스에 속할 확률을 추정하는 데 많이 사용된다, 추정 확률이 50% 가 넘으면 모델은 샘플이 해당 클래스에 속한다고 예측한다. 주로 이진 분류기로 많이 사용된다.

1) 확률 추정

로지스틱 회귀 모델은 입력 특성의 가중치 합을 계산한다. 대신 결과값은 로지스틱으로 출력한다. 일반적으로 로지스틱은 0~1사이의 값을 출력하는 시그모이드 함수로 수식은 다음과 같다.

$\sigma \left(t\right) = \frac {1}{1+\exp \left(-t\right)}$

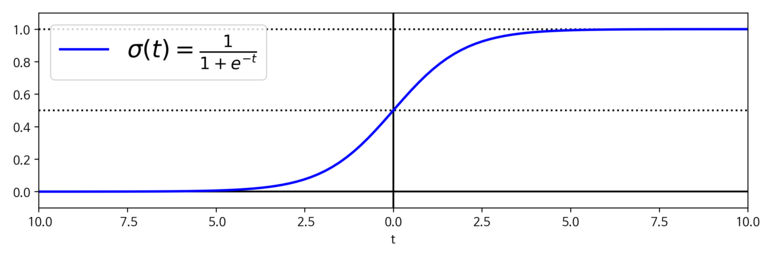
로지스틱 회귀 모델이 샘플 x 가 양성클래스에 속할 확률을 추정하면 아래와 같은 결과를 얻을 것이다.

$ \hat{y}= \begin{cases} 0 & \text{if }\hat{p}<0.5 \ 1 & \text{if }\hat{p}\ge 0.5 \end{cases}$

2) 훈련과 비용함수

훈련의 목적은 양성 샘플(y=1)에 대해 높은 확률을 추정하고 음성샘플(y=0) 에 대해 낮은 확률을 추정하는 모델의 파라미터 벡터인 θ 를 찾는 것이다. 훈련 샘플에 대한 비용함수는 아래와 같다.

$c(\theta)=\begin{cases} -\log (\hat{p}) & \text{if } y=1 \ -\log (1-\hat{p}) & \text{if } y=0 \end{cases}$

비용 함수는 t가 0에 가까워질 수록 -log(t) 가 매우 커지므로 타당하다고 할 수 있다. 따라서 모델이 양성 샘플을 0에 가가운 확률로 추정하면 비율이 크게 증가할 것이다. 반면 t가 1에 가까워질 수록 -log(t)는 0에 가까워진다. 따라서 음성샘플의 확률을 0에 가깝게 추정하거나 양성 샘플의 확률을 1에 가깝게 추정하면 비용은 0에 가까워진다.

비용함수에 대해서는 모든 훈련 샘플의 비용을 평균화 한 것이다. 아래의 수식을 통해 좀 더 살펴보자.

$J\left(\theta \right)=-\frac{1}{m}\sum _{i=1}^m\left[{y}^{\left(i\right)}\log \left({\hat{p}}^{\left(i\right)}\right)+\left(1-{y}^{\left(i\right)}\right)\log \left(1-{\hat{p}}^{\left(i\right)}\right)\right]$

비용함수의 최솟값을 계산하는 알려진 해는 없다. 하지만 볼록 함수이므로 경사하강법이 전역 최소값을 찾는 것을 보장한다.

3) 결정 경계

결정 경계란 분류기가 특성을 기반으로 클래스를 나누는 기준을 의미한다. 좀 더 확실히 알기 위해 우선 붓꽃 데이터를 이용하여 분류기를 만들어보자. 해당 데이터는 붓꽃(Iris)의 3가지 종에 대해 꽃잎과 꽃받침의 너비 및 길이에 대한 데이터를 가지고 있다. 먼저 데이터를 로드 한다.

[Python Code]

from sklearn import datasets

iris = datasets.load_iris()

x = iris["data"][:, 3:]  # 꽃잎 넓이
y = (iris["target"] == 2).astype(np.int)  # Iris-Virginica이면 1 아니면 0

다음으로 로지스틱 회귀 모델을 훈련시킨다.

[Python Code]

from sklearn.linear.model import LogisticRegression

log_reg = LogisticRegression(solver='liblinear', random_state=42)
log_reg.fit(x, y)

학습시킨 모델에 대해 꽃잎의 너비가 0~3cm 인 꽃에 대해서 모델의 추정 확률을 계산해보자.

[Python Code]

x_new = np.linspace(0, 3, 1000).reshape(-1, 1)
y_proba = log_reg.predict_proba(x_new)
decision_boundary = x_new[y_proba[:, 1] >= 0.5][0]

plt.figure(figsize=(8, 3))
plt.plot(x[y==0], y[y==0], "bs")
plt.plot(x[y==1], y[y==1], "g^")
plt.plot([decision_boundary, decision_boundary], [-1, 2], "k:", linewidth=2)
plt.plot(x_new, y_proba[:, 1], "g-", linewidth=2, label="Iris-Virginica")
plt.plot(x_new, y_proba[:, 0], "b--", linewidth=2, label="Not Iris-Virginica")
plt.text(decision_boundary+0.02, 0.15, "결정 경계", fontsize=14, color="k", ha="center")
plt.arrow(decision_boundary, 0.08, -0.3, 0, head_width=0.05, head_length=0.1, fc='b', ec='b')
plt.arrow(decision_boundary, 0.92, 0.3, 0, head_width=0.05, head_length=0.1, fc='g', ec='g')
plt.xlabel("꽃잎의 폭 (cm)", fontsize=14)
plt.ylabel("확률", fontsize=14)
plt.legend(loc="center left", fontsize=14)
plt.axis([0, 3, -0.02, 1.02])

save_fig("logistic_regression_plot")

plt.show()

[실행 결과]

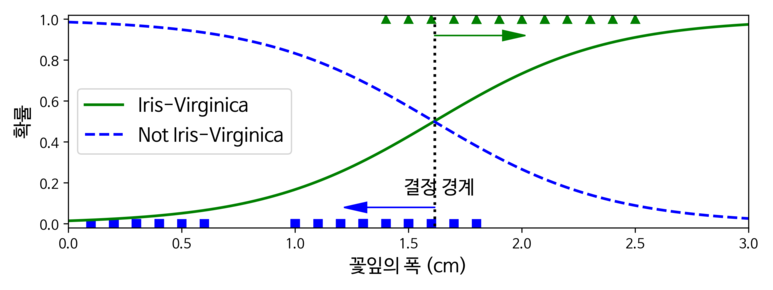
학습한 결과를 보면, 우선 Iris-Virginica는 1.4~2.5cm에 분포한다. 반면 다른 붓꽃의 경우, 일반적으로 꽃잎 너비가 더 작아 0.1~1.8cm 에 분포하는 것을 볼 수 있다. 두 극단 사이에서는 분류가 확실하진 않다. 하지만 클래스를 예측하려고 할 경우 가장 높은 가능성이 있는 클래스를 반환할 것이다. 그렇기 때문에 양쪽의 확률이 똑같이 50%가 되는 1.6cm 근방에서 결정경계가 형성된다.

만약 다음과 같은 입력이 주어진다면 어떻게 분류하는지 살펴보자.

[Python Code]

print(decision_boundary)
print(log_reg.predict([[1.7], [1.5]]))

x = iris["data"][:, (2, 3)]  # petal length, petal width
y = (iris["target"] == 2).astype(np.int)

log_reg = LogisticRegression(solver='liblinear', C=10**10, random_state=42)
log_reg.fit(x, y)

x0, x1 = np.meshgrid(
    np.linspace(2.9, 7, 500).reshape(-1, 1),
    np.linspace(0.8, 2.7, 200).reshape(-1, 1),
)
x_new = np.c_[x0.ravel(), x1.ravel()]

y_proba = log_reg.predict_proba(x_new)

plt.figure(figsize=(10, 4))
plt.plot(x[y==0, 0], x[y==0, 1], "bs")
plt.plot(x[y==1, 0], x[y==1, 1], "g^")

zz = y_proba[:, 1].reshape(x0.shape)
contour = plt.contour(x0, x1, zz, cmap=plt.cm.brg)

left_right = np.array([2.9, 7])
boundary = -(log_reg.coef_[0][0] * left_right + log_reg.intercept_[0]) / log_reg.coef_[0][1]

plt.clabel(contour, inline=1, fontsize=12)
plt.plot(left_right, boundary, "k--", linewidth=3)
plt.text(3.5, 1.5, "Iris-Virginica 아님", fontsize=14, color="b", ha="center")
plt.text(6.5, 2.3, "Iris-Virginica", fontsize=14, color="g", ha="center")
plt.xlabel("꽃잎의 길이", fontsize=14)
plt.ylabel("꽃잎의 폭", fontsize=14)
plt.axis([2.9, 7, 0.8, 2.7])

save_fig("logistic_regression_contour_plot")

plt.show()

[실행결과]

[1.61561562]
[1 0]

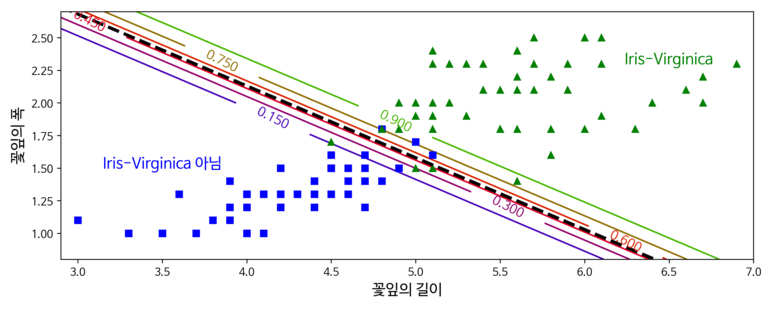
가운데 부분의 진한 점선은 모델이 50% 확률을 추정하는 지점으로 해당 모델의 결정 경계임을 알 수 있다.
다른 모델들과 동일하게 로지스틱 회귀 모델도 L1, L2 페널티를 사용하여 규제할 수있다. 기본적으로는 L2 페널티를 사용한다.

4) 소프트 맥스 회귀

여러 개의 이진 분류기를 훈련 시켜 연결하지 않고 직접 다중 클래스를 지원하도록 로지스틱 회귀를 일반화 한 모형으로 다항 로지스틱 회귀라고도 한다. 샘플 x 가 주어지면 각 클래스 k에 대해 점수를 계산하고 그 점수에 소프트맥스 함수를 적용하여 각 클래스이 확률을 추정한다. 이 때 각 클래스는 자신만을 파라미터 벡터 θ(i) 가 존재하며, 파라미터 벡터 Θ에 행으로 저장된다. 소프트 맥스 함수는 아래의 식과 같다.

$\hat{p}_k=\sigma \left(s\left(x\right)\right)_k=\frac{\exp \left({s}_k\left(x\right)\right)}{\sum _{j=1}^k\exp \left({s}_j\left(x\right)\right)}$

위의 식에서 k는 클래스 개수, s(x)는 샘플 x 에 대한 각 클래스의 점수를 담고 있는 벡터, σ(s(x))k 는 샘플 x 에 대한 각 클래스의 점수가 주어졌을 때, 해당 샘플이 클래스 k에 속할 추정 확률을 의미한다.

소프트 맥스 함수의 목적은 모델이 타깃 클래스에 대해서는 높은 확률을 추정하도록 만드는 것이 목적이다. 크로스 엔트로피 비용 함수를 최소화하는 것은 타깃 클래스에 대해 낮은 확률을 예측하는 모델을 억제하므로 목적에 부함한 함수라고 할 수 있다.
크로스 엔트로피는 추정된 클래스의 확률이 타깃 클래셍 얼마나 잘 맞는지 측정하는 용도로 사용된다. 식은 다음과 같다.

$J\left(\Theta \right)=-\frac{1}{m}\sum _{i=1}^m\sum _{k=1}^K{{y}_k}^{\left(i\right)}\log \left(\hat{p}_k^{\left(i\right)}\right)$

이를 앞서 사용한 붓꽃 데이터에 적용해보자.

[Python Code]

x = iris["data"][:, (2, 3)]  # 꽃잎 길이, 꽃잎 넓이
y = iris["target"]

softmax_reg = LogisticRegression(multi_class="multinomial",solver="lbfgs", C=10, random_state=42)
softmax_reg.fit(x, y)

x0, x1 = np.meshgrid(
    np.linspace(0, 8, 500).reshape(-1, 1),
    np.linspace(0, 3.5, 200).reshape(-1, 1),
)
x_new = np.c_[x0.ravel(), x1.ravel()]

y_proba = softmax_reg.predict_proba(x_new)
y_predict = softmax_reg.predict(x_new)

zz1 = y_proba[:, 1].reshape(x0.shape)
zz = y_predict.reshape(x0.shape)

plt.figure(figsize=(10, 4))
plt.plot(x[y==2, 0], x[y==2, 1], "g^", label="Iris-Virginica")
plt.plot(x[y==1, 0], x[y==1, 1], "bs", label="Iris-Versicolor")
plt.plot(x[y==0, 0], x[y==0, 1], "yo", label="Iris-Setosa")

custom_cmap = ListedColormap(['#fafab0','#9898ff','#a0faa0'])

plt.contourf(x0, x1, zz, cmap=custom_cmap)

contour = plt.contour(x0, x1, zz1, cmap=plt.cm.brg)

plt.clabel(contour, inline=1, fontsize=12)
plt.xlabel("꽃잎의 길이", fontsize=14)
plt.ylabel("꽃잎의 폭", fontsize=14)
plt.legend(loc="center left", fontsize=14)
plt.axis([0, 7, 0, 3.5])

save_fig("softmax_regression_contour_plot")

plt.show()

softmax_reg.predict([[5, 2]])
softmax_reg.predict_proba([[5, 2]])

[실행 결과]

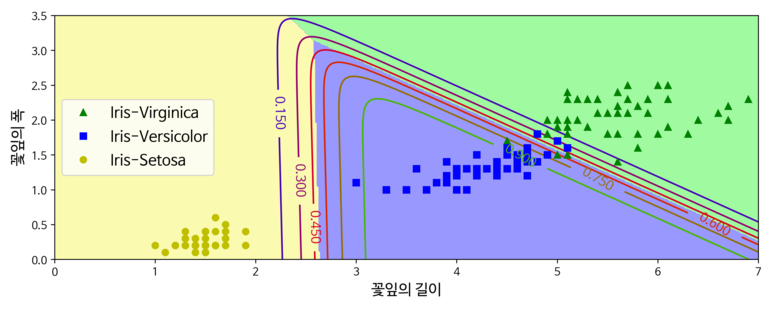
사이킷 런의 Logistic Regression은 클래스가 둘 이상일 때 기본적으로 일대다(OvA) 전략을 사용한다. multi_class 매개변수를 “multinomial”로 바꾸면 소프트맥스 회귀를 사용한다. 만약 소프트맥스 회귀를 사용하려면 solver 매개변수에 “lbfgs”와 같이 소프트맥스 회귀를 지원하는 알고리즘을 지정해야 한다. 기본적으로 하이퍼파라미터 C를 사용하여 조절할 수 있는 L2 규제가 적용된다.