[Python Machine Learning] 12. 데이터 전처리 II : Validation, Scaling, Regulation
1. Data Validation
모델을 실제로 사용하기 전에 테스트 데이터에 있는 레이블(실제 값) 과 모델이 예측한 결과를 비교하게 된다. 이는 모델의 정확한 성능을 측정하기 위해서 수행하는 과정이다. 일반적으로는 학습 데이터 : 테스트 데이터 의 비율을 7 : 3 으로 분할하게된다. 분할할 때 직접 전체 데이터 수를 계산한 다음 70% 는 학습용으로, 30% 는 테스트 용으로 직접 나눌 수도 있겠지만, 매우 번거로운 작업이다.
이를 위해 사이킷 런에서는 train_test_split() 이란 함수를 제공하여, 데이터 분할에 있어 좀 더 용이하도록 한다. 사용법은 다음과 같다. 예시를 위해 UCI 머신러닝 저장소에서 제공하는 Wine 데이터 셋을 활용한다.
[Python Code]
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_wine
df_wine = pd.DataFrame(load_wine().data, columns=load_wine().feature_names)
df_wine_label = pd.DataFrame(load_wine().target, columns=["class"])
df_wine = pd.concat([df_wine, df_wine_label], axis=1)
print(load_wine().DESCR)
print('레이블: ', np.unique(df_wine["class"]))
df_x, df_y = df_wine.iloc[:, 0:12].values, df_wine.iloc[:, 13].values
np.unique(df_y)
x_train, x_test, y_train, y_test = train_test_split(df_x, df_y, test_size=0.3, random_state=0, stratify=df_y)
print(x_train)
print(x_test)
print(y_train)
print(y_test)
[실행 결과]
[[13.62 4.95 2.35 ... 4.4 0.91 2.05]
[13.76 1.53 2.7 ... 5.4 1.25 3. ]
[13.73 1.5 2.7 ... 5.7 1.19 2.71]
...
[[ 13.77 1.9 2.68 17.1 115. 3. 2.79 0.39 1.68
6.3 1.13 2.93 ]
[ 12.17 1.45 2.53 19. 104. 1.89 1.75 0.45 1.03
2.95 1.45 2.23 ]
[ 14.39 1.87 2.45 14.6 96. 2.5 2.52 0.3 1.98
5.25 1.02 3.58 ]
...
[2 0 0 0 2 1 1 2 1 1 1 0 1 2 ...
[0 1 0 0 1 2 1 2 0 2 0 1 2 0 ...
위의 코드 중에서 train_test_split() 함수에 사용된 파라미터에 대해서만 살펴보도록 하자.
먼저 입력으로 학습 대상과 그에 대한 실제 값(레이블) 을 입력으로 받는다. 그다음 등장하는 test_size 파라미터는 테스트 데이터를 학습 데이터에 대해 얼마나 할당할 지를 지정한다. 위의 코드에서는 0.3, 즉, 30% 에 대해서만 x_test, y_test 에 할당한다. 나머지 70%에 대해서는 각각 x_train, y_train 에 할당한다. 다음으로 random_state 는 어떻게 셔플할지를 설정하며, 입력된 값을 이용해 난수를 이용하여 셔플을 하게된다. 마지막으로 stratify 는 클래스 레이블을 전달하게 되면, 훈련 세트와 테스트 세트에 있는 클래스 비율을 원본 데이터셋과 동일하게 유지 시켜준다.
2. Data Scaling
스케일링(Scaling) 이란, 특정 속성의 값 혹은 데이터 셋마다 데이터의 분포가 달라 학습이 원할히 안될 경우, 지정한 값의 범위로 변경해줌으로써 전반적인 데이터의 분포를 맞춰주는 전처리 기법이라고 할 수 있다.
스케일링을 하는 가장 큰 이유는 앞서 언급한 것처럼 데이터의 값이 너무 크거나 혹은 작은 경우 모델의 학습 과정에서 0으로 수렴하거나 무한으로 발산해버릴 수 있기 때문이다. 특히, 거리를 기반으로 하는 머신러닝 모델(kNN, 아달린, SVM 등)의 경우, 학습에 사용된 속성들 중 오차가 큰 특성에 맞춰서 가중치를 최적화하게 되기 때문에 원할하게 학습이 이뤄지지 않는 경우가 많다.
스케일러의 종류는 대표적으로 2가지가 있다. 바로 정규화(Normalization)과 표준화(Standardiztion) 이며, 이번 절에서는 이 두가지에 대해서 살펴보도록 하자.
1) 정규화 (Normalization)
일반적으로 정규화는 속성 값의 범위를 0 ~ 1 사이의 값으로 맞추는 작업을 의미하며, 최소-최대 스케일 변환 중 특수한 경우라고 할 수 있다. 최소-최대 스케일 변환은 아래의 수식과 같이 값을 조정한다.
$x_{norm}^{(i)} = \frac {x^{(i)} - x_{min}} { x_{max} - x_{min} } $
위의 식에서 $ x^{(i)} $ 는 특정 샘플이고, $ x_{max} $ 는 속성 값 중 가장 큰 값, $ x_{min} $ 은 속성 값 중 가장 작은 값을 의미한다. 위의 내용을 사이킷런에서는 아래의 코드와 같이 구현할 수 있다.
[Python Code]
from sklearn.preprocessing import MinMaxScaler
from sklearn.datasets import load_iris
iris = load_iris()
x = iris.data
y = iris.target
scaler = MinMaxScaler()
x_norm = scaler.fit_transform(x)
[실행 결과]
...
[0.52777778 0.58333333 0.74576271 0.91666667]
[0.44444444 0.41666667 0.69491525 0.70833333]]
2) 표준화 (Standardization)
최소-최대 스케일 변환을 통한 정규화는 범위가 정해진 값이 필요할 때 유용하게 사용할 수 있었다면, 표준화는 좀 더 범용적으로 머신러닝 알고리즘에서 사용될 수 있다. 표준화를 사용하게되면, 정규분포와 유사하게 평균은 0에 , 표준편차는 1에 가깝게 만든다. 이로 인해 가중치를 더 쉽게 학습할 수 있고, 이상치 정보가 표준화 적용 전후와 비교했을 때, 그대로 유지되기 때문에 앞서 본 최소-최대 스케일 변환 기법보다 이상치에 덜 민감하다. 수학적으로 표현하면 아래와 같다.
$ x_{std}^{(i)} = \frac {x^{(i)} - {\mu }_x} { {\sigma }_x } $
위의 수식에서 $ {\mu}_x $ 는 특성 샘플의 평균을 의미하고. $ {\sigma }_x $ 는 특성 샘플의 표준편차를 의미한다. 표준화와 정규화의 차이를 아래 예시를 통해서 확인해보자.
[Python Code]
import numpy as np
sample = np.array([0,1,2,3,4,5])
print("표준화 결과: ", (sample - sample.mean()) / sample.std())
print("정규화 결과: ", (sample - sample.min()) / sample.max() - sample.min())
[실행 결과]
표준화 결과: [-1.46385011 -0.87831007 -0.29277002 0.29277002 0.87831007 1.46385011]
정규화 결과: [0. 0.2 0.4 0.6 0.8 1. ]
이제 앞서 본 표준화에 대한 내용을 scikit-learn 을 이용해 구현하는 방법을 살펴보자.
[Python Code]
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
x_standard = scaler.fit_transform(x)
print(x_standard)
[실행 결과]
[[-9.00681170e-01 1.01900435e+00 -1.34022653e+00 -1.31544430e+00]
[-1.14301691e+00 -1.31979479e-01 -1.34022653e+00 -1.31544430e+00]
[-1.38535265e+00 3.28414053e-01 -1.39706395e+00 -1.31544430e+00]
참고로 fit 메소드는 훈련 데이터에 한 번만 적용시켜주고 나면, 이후에 차원이 동일한 다른 데이터에 대해서도 굳이 fit 메소드를 실행할 필요 없이, 바로 transform 메소드를 사용할 수 있다.
3. Data Regulation
규제(Regulation)란, 데이터에 과대적합을 방지하기 위한 방법 중 하나로, 모델이 학습하는 데 사용되는 가중치에 규제 값을 주어 과적합이 되는 것을 막고, 일반화에 도움을 주기 위한 방법이라고 할 수 있다.
여기서, 과대적합(Overfitting) 이란, 모델이 학습데이터에 너무 치중되도록 학습을 해서, 학습 데이터에 대한 예측 은 잘 되는 반면, 실제 예측해야되는 데이터를 정확히 예측하지 못하는 현상을 의미한다.
과대적합이 발생하는 요인은 아래와 같이 크게 2가지로 볼 수 있다.
과대적합의 원인
- 모델 자체가 너무 복잡한 경우
- 데이터가 학습을 하기에 너무 적은 경우
해결방법은 많이 있지만, 그 중에서 이번에는 가중치에 규제를 줌으로써, 과대적합을 방지하는 방법에 대해 알아보자.
1) Norm
본격적으로 설명하기에 앞서 norm 이라는 용어를 우선 살펴보자. 먼저, Norm 이란, 벡터의 크기(혹은 길이)를 측정하는 방법이다. 수식으로 표현하면 아래와 같다.
$ {\Vert{X}\Vert}_p := {(\sum _{i=1}^n {\vert{x_i}\vert}^p)}^{\frac {1}{p}} $
norm 에는 크게 2가지 방식이 있는데, L1 norm 은 두 벡터들의 원소들의 차이에 대한 절대값의 합으로 계산한다.
반면 L2 norm 은 두 벡터간의 유클리디안 거리로 계산한다.
$L_1norm = \Vert{p_i - q_i}\Vert = \sum _{i=1}^n \vert{p_i - q_i}\vert $
$L_2norm = \Vert{x_i}\Vert = \sqrt {\sum _{i=1}^n x_i^2} $
위의 수식에서 p 와 q 는 모두 두 벡터의요소 라고 가정하며, $x_i = p_i - q_i$ 이고, 이 때 $p = (x_1, x_2, x_3, …)$ 이고, $q = (0, 0, 0, …)$ 이라고 가정한다.
2) Loss
Loss 라는 것은 실제 값과 예측 값 사이의 오차를 의미한다. Norm 과 마찬가지로 L1 Loss와 L2 Loss 가 존재하며,
L1 Loss 는 실제 값과 예측 값 사이의 차이에 대한 절대 값의 합으로 계산된다. 반면 L2 Loss 는 오차의 제곱합으로 계산된다.
$ Loss_{L1} = \sum _{i=1}^n \vert {y_i - f(x_i)} \vert $
$ Loss_{L1} = \sum _{i=1}^n {(y_i - f(x_i))}^2 $
3) L1 Regulation
L1 규제의 핵심은, 손실함수에 가중치의 절대값에 학습률과 같은 상수 λ 를 곱하고, 1/2 또는 1/n 으로 나누어 주는데, 이 때 상수 λ 값이 작을 수록 규제의 효과는 없어진다. 회귀에서는 L1 규제를 사용하는 회귀모형을 가리켜, Lasso 회귀 라고 부른다.
$ Cost =\frac {1} {n} \sum _{i=1}^n L(y_i, {\hat {y}}_i) + \frac {\lambda } {2} \vert{w}\vert $
앞서 언급한 대로 L1 규제는 가중치 절대값의 합이기 때문에 아래와 같이 다이아몬드 모양의 제한 범위를 그릴 수 있다.
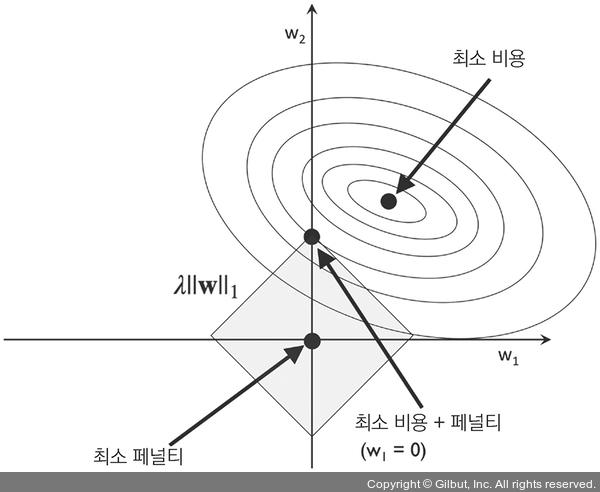
위의 그림에서 규제 파라미터는 λ 값으로, 값을 크게 줄 경우, 가중치는 0에 가까워지고, 훈련 데이터에 대한 모델의 존성은 줄어든다. 또한 가중치 값은 규제 영역보다 바깥에 놓일 수는 없다. 때문에 페널티가 존재하는 상황에서 가장 최선이 되는 조건은 손실함수의 접점이 제한영역의 외곽선 위에 존재하는 경우이다.
L1 규제의 경우, 다이아몬드 형태이기 때문에, 비용함수의 등고선은 L1 규제와 만나는 지점이 거의 축에 위치할 확률이 높다. 때문에 최적점이 축에 가깝게 위치할 확률이 높다.
scikit-learn 에서 L1 규제를 사용하려면 아래와 같이 작성하면 된다. 예시를 위해 모델의 앞쪽 파라미터는 생략했다.
[Python Code]
from sklearn.linear_model import LogisticRegression
model = LogisticRegression(..., penalty='L1')
4) L2 Regulation
L2 규제의 핵심은 손실함수의 가중치에 제곱을 포함해서 더하기 때문에 L1 규제와 마찬가지로 가중치가 너무 크지 않은 방향으로 학습하게 된다. 회귀에서는 L2 규제를 사용하는 회귀모형을 가리켜, Ridge 회귀라고 부른다.
L2 규제에 대한 수식은 다음과 같다.
$ Cost = \frac {1} {n} \sum _{i=1}^n L(y_i, {\hat {y}}_i) + \frac {\lambda } {2} \vert{w}\vert^2 $
위에서 설명한 것처럼, L2 규제는 가중치의 제곱을 더해주기 때문에 아래 그림과 같이 원형의 제한 영역이 그려진다.
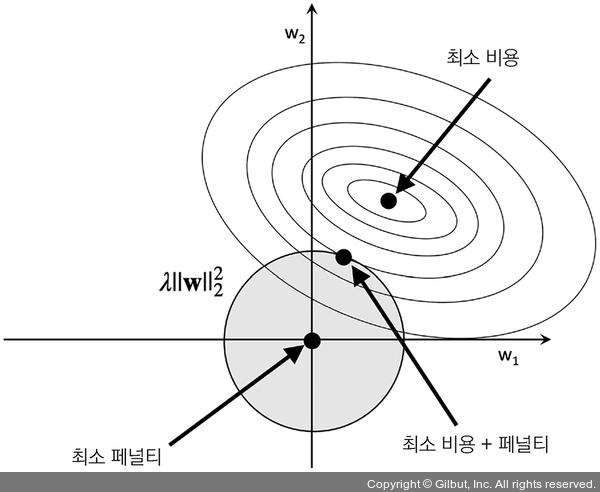
L2 규제의 경우, 위의 그림에서 처럼 원형으로 표시되기 때문에 비용함수와 만나는 접점은 두 원의 접점과 동일하다. 위의 내용을 scikit-learn으로 구현하면 다음과 같다.
[Python Code]
from sklearn.linear_model import LogisticRegression
model = LogisticRegression(..., penalty='L2')
이렇듯, 모델이 학습할 만한 충분한 훈련 데이터가 없을 경우, 편향(규제항) 을 이용해서 모델을 생성하게 되면, 분산이 줄어들기 때문에 학습하는 데에 좀 더 용이하다고 할 수 있다.
[참고자료]
머신러닝 교과서 with 파이썬,사이킷런,텐서플로 (길벗 출판사)
https://thebook.io/007022
https://thebook.io/007022
https://light-tree.tistory.com/125

댓글남기기