[Python Machine Learning] 1. 파이썬 데이터 관리 & 머신러닝의 시작
1. Numpy
1) ndarray (다차원 배열 객체)
N 차원 배열 객체로, 같은 종류의 데이터를 담을 수 있는 다차원 배열(모든 원소는 같은 자료형)이다.
모든 배열은 각 차원의 크기를 알려주는 shape라는 튜플과 배열에 저장된 자료형을 알려주는 dtype 객체를 가지고 있다.
ndarray의 astype 메소드를 이용해 배열의 dtype을 다련 형으로 명시적 변경이 가능하다.
[Python Code]
data1 = [6, 7.5, 8, 0, 1]
arr1 = np.array(data1)
data2 = [[1,2,3,4],[5,6,7,8]]
arr2 = np.array(data2)
arr2.ndim
arr2.shape
arr1.dtype
arr2.dtype
2) 표준 배열 생성 함수
초기화할 경우에 사용하며 사용되는 함수들은 아래와 같다.
-
array
입력 데이터(리스트, 튜플, 배열 또는 다른 열거형 데이터)를 ndarray로 변환하며, dtype이 명시되지 않은 경우에는 자료형을 추론하여 저장하며 기본적으로 입력 데이터는 복사한다. -
as.array
입력 데이터를 ndarray로 변환하지만 입력 데이터가 이미 ndarray일 경우에는 복사되지 않는다. -
arrange
range 함수와 유사하지만 리스트가 아닌 ndarray를 반환한다. -
ones (like)
주어진 dtype과 주어진 모양을 가지는 배열을 생성하고 내용을 모두 1로 초기화함
ones like의 경우 주어진 배열의 동일한 모양과 dtype을 가지는 배열을 새로 생성하여 내용을 모두 1로 초기화함 -
zero (like)
ones (like)와 유사하지만 초기화를 0으로 한다.
[Python Code]
arr = np.array([1,2,3,4,5])
arr.dtype
float_arr = arr.astype(np.float64)
float_arr.dtype
arr = np.array([3.7, -1.2, -2.6, 0.5, 12.9, 10.1])
arr
arr.astype(np.int32)
3) 인덱스와 슬라이싱 기초
표면적으로는 리스트와 유사하게 동작함
[Python Code]
arr = np.arange(10)
arr
arr[5]
arr[5:8]
arr[5:8] = 12
arr
# 리스트와의 차이점
list1 = list(range(5))
list2 = list1[0:3]
arr1 = np.arange(5)
arr2 = arr[0:3]
list2[1] = 0
arr2[1] = 0
list1
arr1
2차원 배열에서 각 인덱스에 해당하는 요소는 스칼라값이 아니라 1차원 배열로 저장된다.
[Python Code]
arr2d = np.array([[1,2,3],[4,5,6],[7,8,9]])
arr2d[2]
arr2d[0][2]
arr2d[0,2]
arr3d = np.array([[[1,2,3],[4,5,6]],[[7,8,9],[10,11,12]]])
arr3d
arr3d[0]
4) 슬라이스 인덱스
[Python Code]
arr2d
arr2d[:2]
arr2d[:2,1:]
arr2d[1,:2]
arr2d[2,:1]
arr2d[:,:1]
5) 불리언 인덱스
[Python Code]
names = np.array(['Bob','Joe','Will','Bob','Will','Joe','Joe'])
data = np.arange(28).reshape(7,4)
data[names == 'Bob']
data[names == 'Bob',1]
data[names == 'Bob',3]
data[data < 5] = 0
data
6) 펜시 인덱스
[Python Code]
arr = np.zeros((8,4))
for i in range(8):
arr[i] = i
arr[[4,3,0,6]]
arr[[-3,-5,-7]]
arr = np.arange(32).reshape((8,4))
arr[[1,5,7,2],[0,3,1,2]]
arr[[1,5,7,2]][:,[0,3,1,2]]
arr[np.ix_([1,5,7,2],[0,3,1,2])]
7) 유니버셜 함수
ndarray 안에서 요소 별로 연산을 수행하는 함수
[Python Code]
arr = np.arange(18)
np.sqrt(arr)
np.exp(arr)
x = np.random.randn(8)
y = np.random.randn(8)
np.maximum(x,y)
8) 배열연산으로 조건절 표현하기
np.where() 함수는 ‘x if 조건 else y’ 와 동일하며, C언어의 삼항 연산자와 동일하다.
[Python Code]
np.where(arr > 1,1,0)
9) 수학 메소드 & 통계 메소드
[Python Code]
arr = np.random.randn(5,4)
arr
arr.mean()
np.mean(arr)
arr.sum()
arr.mean(axis = 1) # 축을 따라 계산 / 0: 행별로 , 1: 열별로
arr.cumsum(0) # 누적 합
arr.cumprod(1) # 누적 곱
2. Pandas
Numpy를 기반으로 개발된 고수준의 자료구조인 data.frame을 이용할 수 있는 라이브러리
[Python Code]
from pandas import Series, DataFrame
import pandas as pd
1) Series
1차원 배열 같은 자료구조이나 index를 가지고 있으며, 인덱스로 값을 참조한다.
인덱스는 직접지정이 가능하다. 또한 지정해 둔 인덱스로 값을 찾는 것 뿐만 아니라 멤버쉽 테스트도 가능하다.
만약 값이 없다면 NaN 으로 채워넣는다.
※ NaN, NA : 값이 없음을 의미
[Python Code]
import pandas as pd
from pandas import Series, DataFrame
obj = Series([4, 7, -5, 3])
obj
obj.values
obj.index
obj2 = Series([4,7,-5,3], index = ['d','b','a','c'])
obj2
obj2.index
obj2['a']
obj2['d']=6
obj2[['c','a','d']]
obj2[obj2 > 0]
obj2 * 2
np.exp(obj2)
# Membership Test
'b' in obj2
'e' in obj2
2) DataFrame
데이터 프레임의 각 열은 서로 다른 종류의 값을 가질 수 있다. ndarray가 하나의 자료형만 가질 수 있는 반면 데이터 프레임은 열마다 다른 값을 가질 수 있고 행과 열에 대한 인덱스가 존재한다.
인덱스가 동일한 여러 개의 Series 객체를 가지고 았는 사전이다.
[Python Code]
data = {'state' : ['Ohio',' Ohio','Ohio','Nevada','Nevada'],
'year' : [2000, 2001, 2002, 2001, 2002],
'pop' : [1.5, 1.7, 3.6, 2.4, 2.9]}
frame = DataFrame(data)
DataFrame(data, columns = ['year','state','pop'])
frame2 = DataFrame(data, columns=['year','state','pop','debt'], index=['one','two','three','four','five'])
frame2.columns
frame2['state'] # 괄호안의 u는 유니코드의 기호이다.
frame2.year
frame2.ix['three']
frame2['debt'] = 16.5
frame2['debt'] = np.arange(5.)
val = Series([-1.2,-1.5,-1.7], index = ['two','three','four'])
frame2['debt'] = val
frame['eastern'] = frame2.state == 'Ohio'
pop = {'Nevada': {2001: 2.4, 2002: 2.9}, 'Ohio': {2000: 1.5, 2001: 1.7, 2002: 3.6}}
frame3 = DataFrame(pop)
frame3
frame3.T
frame3 = DataFrame(pop, index=[2001,2002,2003])
frame3.values
frame2.values
(1) 인덱스 객체
슬라이스 한 부분은 변경 불가하다.
[Python Code]
obj = Series(range(3), index=['a','b','c'])
index = obj.index
index
index[1:]
index[1] = 'd'
(2) reindex
[Python Code]
frame = DataFrame(np.arange(9).reshape((3, 3)), index=['a','c','d'], columns=['Ohio','Texas','California'])
frame
frame2 = frame.reindex(['a','b','c','d'])
frame2
states = ['Texas','Utah','California']
frame.reindex(columns=states)
(3) 하나의 행 또는 열 삭제
[Python Code]
obj = Series(np.arange(5.), index=['a','b','c','d','e'])
new_obj = obj.drop('c') # 기본 인덱스(행)을 지움
new_obj
obj.drop(['d','c'])
data = DataFrame(np.arange(16).reshape((4,4)), index=['Ohio','Colorado','Utah','New York'], columns=['one','two','three','four'])
data.drop(['Colorado','Ohio'])
data.drop(['Colorado','Ohio'])
data.drop('two', axis=1) # 열 삭제 (삭제할 열의 이름 입력,axis=1)
data.drop(['two','four'], axis=1)
(4) indexing , selecting
펜시 슬라이스와 동일한 방식으로 동작한다.
[Python Code]
data = DataFrame(np.arange(16).reshape((4,4)), index=['Ohio','Colorado','Utah','New York'], columns=['one','two','three','four'])
data['two']
data[['three','one']]
data[:2]
data[data['three'] > 5]
data.ix['Colorado', ['two','three']]
data.ix[['Colorado','Utah'], [3,0,1]]
data.ix[2]
data.ix[:'Utah','two']
data.ix[data.three > 5, :3]
(5) 함수 적용과 매핑
[Python Code]
frame = DataFrame(np.random.randn(4, 3), columns = list('bde'), index=['Utah','Ohio','Texas','Oregon'])
frame
np.abs(frame)
f = lambda x : x.max() - x.min() #lambda : 한 줄짜리 함수
frame.apply(f)
frame.apply(f, axis=1)
(6) 정렬
[Python Code]
obj = Series(range(4), index=['d','a','b','c'])
obj.sort_index()
frame = DataFrame(np.arange(8).reshape((2,4)), index=['three','one'], columns=['d','a','b','c'])
frame.sort_index()
frame.sort_index(axis=1) # 열 별로 정렬
frame.sort_index(axis=1, ascending=False) # 내림차순으로 정렬
(7) 중복 인덱스
중복을 허용하기 때문에 유일성은 존재하지 않는다.
[Python Code]
obj = Series(range(5), index=['a','a','b','b','c'])
obj
obj['a']
obj['c']
df = DataFrame(np.random.randn(4, 3), index=['a','a','b','b'])
df
df.ix['b'] # b 행만 선택하고 싶은 경우
(8) 기술통계 계산과 요약
- df.describe()
모든 변수에 대해 모든 기술 통계값을 계산해준다.
문자열에도 적용가능하다.
다른 기술 통계향을 계산해준다.
[Python Code]
df = DataFrame([[1.4, np.nan], [7.1, -4.5], [np.nan, np.nan], [0.75,-1.3]], index=['a','b','c','d'], columns=['one','two'])
df
df.sum()
df.sum(axis=1)
df.mean(axis=1, skipna=False) # nan 를 제거하지않고 하고 싶은 경우 skipna=false로 해주면된다.
df.cumsum()
df.describe()
(9) 누락된 데이터 처리하기
[Python Code]
from numpy import nan as NA
string_data = Series(['aardvark','artichoke',np.nan,'avocado'])
string_data
string_data.isnull()
string_data[0] = None
string_data.isnull()
# phase 1. 누락된 데이터 골라내기
data = Series([1,NA,3.5,NA,6])
data.dropna() # na인 값들을 제거
data[data.notnull()] # na가 아닌 값들만 남음
data = DataFrame([[1., 6.5, 3.], [1.,NA,NA], [NA,NA,NA], [NA,6.5,3.]])
cleaned = data.dropna()
data
cleaned
data.dropna(how='all') # 한 행이 모두 na인 행만 제거
data[4] = NA
data
data.dropna(axis=1, how='all') # 열 축을 기준으로 모든 값이 na 인 값 제거
Df = DataFrame(np.random.randn(7,3))
Df.ix[:4, 1] = NA
Df.ix[:2, 2] = NA
df
df.dropna(thresh=3)</pre>
# phase 2. 누락된 값 채우기
df.fillna(0)
df.fillna({1:0.5,3:-1}) # na를 -1로 채움
df.fillna(0, inplace=True) # 본래 값을 바꿔줄 수 있다.
3. SciPy
Numpy의 효율적인 데이터 구조 위에서 SciPy는 이러한 배열을 효율적으로 처리하는 매트릭스 처리, 선형대수, 최적화, 군집화, 공간 연산, 고속 퓨리에 변환 등 수많은 알고리즘을 제공한다.
수치 알고리즘을 이용할 때 사용하는 것이 좋고, 편의상, Numpy는 네임스페이스는 SciPy로 접근 가능하다.
4. 데이터 읽고 쓰기
1) 텍스트 파일을 이용하기
[Python Code]
import pandas as pd
from pandas import Series, DataFrame
result = pd.read_csv('ch06/ex5.csv')
result
pd.isnull(result) # null값이 있는지 확인
# 결측값을 원하는 값으로 바꿀 경우: NULL자리에 원하는 값을 입력하면 된다.
result = pd.read_csv('ch06/ex5.csv', na_values=['NULL'])
# 데이터 구조에 대한 내용 출력 R에서 structure()(or str() )와 유사함
result
result.info()
sentinels = {'message': ['foo', 'NA'], 'something' : ['two']} # messag에서는 foo와 NA를 , something에서는 two를 결측값으로 처리
# na_values는 해당변수를 null로 결측값을 처리
pd.read_csv('ch06/ex5.csv', na_values=sentinels)
2) 텍스트 파일 조금씩 읽어오기
[Python Code]
result = pd.read_csv('ch06/ex6.csv')
result
# nrows: 해당 숫자만큼 데이터를 읽어옴.
pd.read_csv('ch06/ex6.csv', nrows=5)
# 데이터를 쪼개기 / 값은 나오지 않음. 대신 chunker 객체만 생성
chunker = pd.read_csv('ch06/ex6.csv', chunksize=1000)
tot = Series([])
for piece in chunker:
tot = tot.add(piece['key'].value_counts(), fill_value=0)
tot = tot.order(ascending=False)
3) 데이터를 덱스트 형식으로 기록하기
R 방식과 유사하다.
[Python Code]
data = pd.read_csv('ch06/ex5.csv')
data
data.to_csv('out.csv') #현재 작업 디렉토리에 저장->파일명앞에 경로명 넣을 경우 해당 경로에 파일저장 Ex. data.to_csv(‘c:\out.csv’)
data.to_csv('out2.csv', sep='|')
data.to_csv('out3.csv', na_rep='NULL')
data.to_csv('out4.csv', index=False, header=False) # Index(또는 header)를 true로 지정하면 행(또는 열)의 이름까지 생성
data.to_csv('out5.csv', index=False, columns=['a','b','c']) #열 이름을 직접 지정 가능 / a, b, c 열만 나옴
5. 데이터 변형
1) 데이터 병합
-
pandas.merge
하나 이상의 키를 기준으로 DataFrame의 행을 합침 → 교집합 구하기
merge는 기본적으로 교집합 how 인지를 통해 left, rigth, outer가 가능한다. -
how
더 포함사고 싶은 내용으로 추가하고자 할 때 사용한다. -
suffixes
데이터의 출처를 밝히고 싶은 경우에 사용한다.
[Python Code]
df1 = DataFrame({'key': ['b','b','a','c','a','a','b'], 'data1': range(7)})
df2 = DataFrame({'key': ['a','b','d'], 'data2': range(3)})
df3 = DataFrame({'lkey': ['b','b','a','c','a','a','b'], 'data1': range(7)})
df4 = DataFrame({'rkey': ['a','b','d'], 'data2': range(3)})
pd.merge(df3,df4,left_on='lkey',right_on='rkey')
2) 축 따라 이어붙이기
-
pandas.concat
축에 따라 이어 붙인다
pandas에서의 concat은 NumPy 에서의 concatenate 함수와 같음 -
ignore_index
인덱스를 기준으로 더하고 싶지만 재색인을 하는 경우에 새로 인덱스를 생성한다.
[Python Code]
arr = np.arange(12).reshape((3,4))
arr
np.concatenate([arr,arr], axis=1)
s1 = Series([0,1], index=['a','b'])
s2 = Series([2,3,4], index=['c','d','e'])
s3 = Series([5,6], index=['f','g']) # 아래로 값이 입력되는 이유 ->axis = 0 이어서
pd. Concat([s1, s2, s3])
pd. Concat([s1, s2, s3], axis=1)
s4 = Series([s1 * 5, s3])
pd. Concat([s1, s4], axis=1)
pd. concat([s1, s4], axis=1, join='inner')
3) 곂치는 데이터 합치기
[Python Code]
a = Series([np.nan, 2.5, np.nan , 3.5, 4.5, np.nan], index=['f','e','d','c','b','a'])
b = Series(np.arange(len(a), dtype=np.float64), index=['f','e','d','c','b','a'])
b[-1] = np.nan
# 삼항연산자
np.where(pd.isnull(a), b, a)
# 위에 있는 where 메소드와 동일하다. 하지만 어려우므로 where메소드를 사용하자
b[:-2].combine_first(a[2:])
4) 중복 제거하기
[Python Code]
data = DataFrame({'k1': ['one'] * 3 + ['two'] * 4, 'k2' : [1,1,2,3,3,4,4]})
data
data.duplicated() # 내용이 중복되는지를 확인(Boolean 값을 반환)
data.drop_duplicates() # 중복되는 내용을 완전 제거(최초 검색된 값만 남음
data.drop_duplicates(['k1','k2'], take_last=True) # 마지막 중복된 값을 남김
5) 함수나 매핑을 이용해 데이터 변형하기
[Python Code]
data = DataFrame({'food':['bacon', 'pulled pork','bacon', 'Pastrami','corned beef','Bacon','pastrami','honey ham','nova lox'], 'ounces': [4,3,12,6,7.5,8,3,5,6]})
data
meat_to_animal = {'bacon': 'pig','pulled pork': 'pig','pastrami': 'cow','corned beef': 'cow','honey ham': 'pig','nova lox': 'salmon'}
data['animal'] = data['food'].map(str.lower).map(meat_to_animal)
data['food'].map(lambda x: meat_to_animal[x.lower()])
6) 값 치원하기
replace 메소드를 사용한다.
[Python Code]
data = Series([1., -999., 2., -999., -1000., 3.])
data
data.replace(-999, np.nan)
data.replace([-999,-1000], np.nan)
data.replace([-999,-1000], [np.nan,0]) # 각각 적용
data.replace({-999: np.nan, -1000: 0}) # 위의 명령과 동일
df = DataFrame(np.arange(5*4).reshape(5,4))
sampler = np.random.permutation(5)
sampler
df.ix[sampler] # 행을 인덱스로 찾고 싶을 때
df.take(sampler) # 위의 결과와 동일
7) 더미 변수
[Python Code]
df = DataFrame({'key' : ['b','b','a','c','a','b'],'data1' : range(6)})
pd.get_dummies(df['key']) #가변수를 생성하는 함수 / 명목 변수를 생성 그룹간의 효과를 보기 위해 카테고리를 만들어 지시자 역할을 하는것
dummies = pd.get_dummies(df['key'] , prefix='key')
df_with_dummy = df[['data1']].join(dummies)
5. 데이터 정리와 전처리
여기서는 Scipy를 이용한 예제를 사용함
[Python Code]
import scipy as sp
import matplotlib.pyplot as plt
data = sp.genfromtxt("data/web_traffic.tsv", delimiter = "\t")
print(data[:10])
print(data.shape)
x = data[:,0]
y = data[:,1]
sp.sum(sp.isnan(y))
x = x[~sp.isnan(y)]
y = y[~sp.isnan(y)]
# 시각화
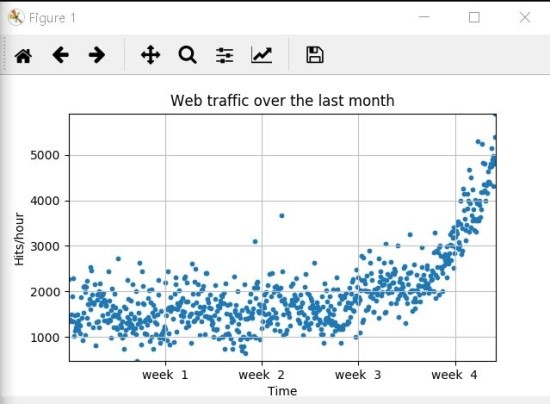
plt.scatter(x,y,s =10)
plt.title("Web traffic over the last month")
plt.xlabel("Time")
plt.ylabel("Hits/hour")
plt.xticks([w*7*24 for w in range(10)], ['week % i' % w for w in range(10)])
plt.autoscale(tight=True)
plt.grid(True, linestyle='-', color = '0.75')
plt.show()
6. 적절한 모델과 알고리즘
1) 근사치 오차
복잡한 현실의 이론적 근사치로서 단순화된 모델과 현실의 차이를 의미하며, 모델이 예측한 예상 값과 실제 값 사이의 거리 제곱으로 계산한다.
2) 단순한 직선으로 시작하기
근사치 오차가 가장 작도록 직선을 그리는 것이 목적이며, 이번 예제에서는 Scipy의 plotfit() 함수를 이용해서 수행한다.
다항 함수의 차수를 고려해 이전에 정의했던 오차를 최소로 만드는 모델함수를 찾는다. 아래 코드에서 사용된 polyfit() 함수는 적합화된 모델 함수 fp1의 매개변수를 반환한다.
full을 True로 설정하면 적합화하는 과정의 추가적인 정보를 얻을 수 있다.
[Python Code]
# 근사치 오차 함수 생성
def error(f, x, y):
return sp.sum((f(x) - y)**2)
# 단순 직선으로 시작하기
fp1, residuals, rank, sv, rcond = sp.polyfit(x, y, 1, full=True)
print("Model parameters: %s" % fp1)
print(residuals)
# f(x) = 2.59619213 * x + 989.02487106
f1 = sp.poly1d(fp1)
print(error(f1, x, y))
fx = sp.linspace(0,x[-1],1000)
plt.plot(fx,f1(fx),linewidth=4)
plt.legend(["d = %i" % f1.order], loc = "upper left")
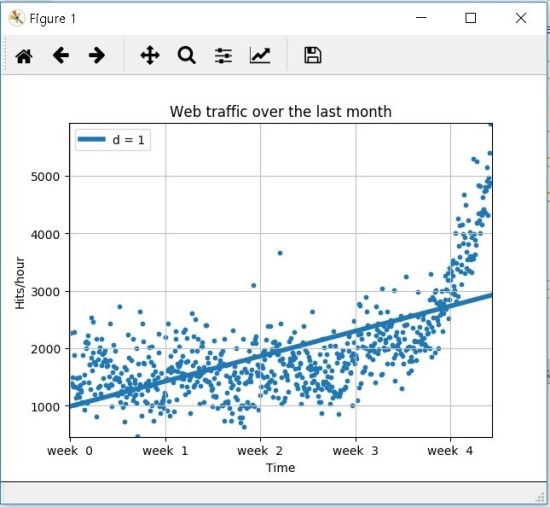
- 직선 함수 식: $\f(\x) = \2.59619213\x \ + \989.02487106
- 오차 : 317,189,767.34
→ 일반적으로 오차 절대값은 비교하는데 사용된다
→ 두 경쟁 모델을 비교해, 어떤 모델이 나은지 판단할 때 사용된다.
3) 좀 더 복잡한 모델
앞선 모델과 비교하기 위해서 새로운 선형모델은 이용해 본다.
[Python Code]
f2p = sp.polyfit(x, y, 2)
print(f2p)
f2 = sp.poly1d(f2p)
print(error(f2, x, y))
# f(x) = 0.0105322215 * x**2 - 5.26545650 * x + 1974.76082
plt.plot(fx,f2(fx),linewidth=4)
파란색 선형 모형보다 주황색 선형 모형이 좀 더 잘 분류해 낸다는 사실을 알 수 있다.
다음으로 주황색 선형모형의 방정식을 보면 다음과 같다.
$f\left(x\right)\ =\ 0.0105322215{x}^2\ -\ 5.26545650x\ +\ 1974.76082$
직선형 모형의 오차보다 거의 절반인 179983507.878의 값을 가지기 때문에 좀 더 정확하게 분류한다는 것의 의미한다.
[Python Code]
f3p = sp.polyfit(x, y, 3)
f10p = sp.polyfit(x, y, 10)
f53p = sp.polyfit(x, y, 53)
print(f3p)
print(f10p)
print(f53p)
f3 = sp.poly1d(f3p)
f10 = sp.poly1d(f10p)
f53 = sp.poly1d(f53p)
print(error(f3, x, y))
print(error(f10, x, y))
print(error(f53, x, y))
plt.plot(fx,f3(fx),linewidth=4)
plt.plot(fx,f10(fx),linewidth=4)
plt.plot(fx,f53(fx),linewidth=4)
plt.legend(["d = %i" % f1.order,"d = %i" % f2.order,
"d = %i" % f3.order, "d = %i" % f10.order,
"d = %i" % f53.order], loc = "upper left")
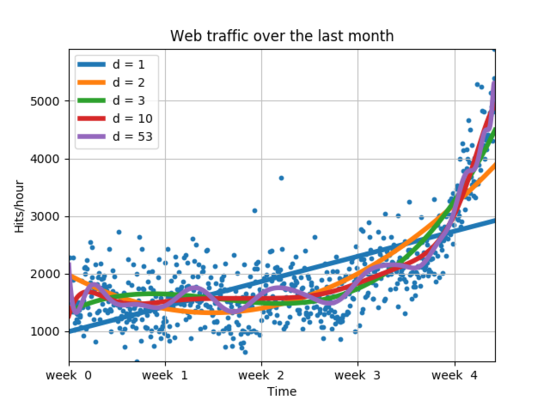
100까지 실행할 경우 “ RankWarning: Polyfit maybe poorly conditioned “와 같은 경고 메세지를 볼 수 있기 때문에 53으로 맞춘 것이다.
이는 복잡한 데이터를 입력 받을수록 곡선은 이를 반영해 좀 더 적합해지며 오차 또한 동일한 결과를 보여준다고 볼 수 있다.
하지만 d = 53의 경우에는 데이터에 너무 잘 맞는 “과적합화(Overfitting)” 현상이 보이는 것을 알 수 있다. 때문에 다음의 경우 중 한 가지를 선택해야된다.
- 적합화된 다항식 모델 중 하나를 선택
- 스플라인 같은 좀 더 복잡한 모델로 변경
- 데이터를 다르게 분석하고 다시 시작
4) 데이터 재검토
주어진 데이터를 보면 Week 3와 Week 4 사이에 변공점이 존재한다. 때문에 3.5 주차를 기준으로 데이터를 둘로 나누고 따로 훈련 시킨다.
[Python Code]
inflection = (int)(3.5 * 7 * 24) # 슬라이스 되는 것은 int형의 값으로 해야되기 때문
xa = x[:inflection]
ya = y[:inflection]
xb = x[inflection:]
yb = y[inflection:]
fa = sp.poly1d(sp.polyfit(xa,ya,1))
fb = sp.poly1d(sp.polyfit(xb,yb,1))
fa_error = error(fa, xa, ya)
fb_error = error(fb, xb, yb)
print("Error inflection = %f" % (fa_error + fb_error))
fap = sp.polyfit(xa, ya, 1)
fbp = sp.polyfit(xb, yb, 1)
fa1 = sp.poly1d(fap)
fb1 = sp.poly1d(fbp)
plt.scatter(x,y,s =10)
plt.title("Web traffic over the last month")
plt.xlabel("Time")
plt.ylabel("Hits/hour")
plt.xticks([w*7*24 for w in range(10)], ['week % i' % w for w in range(10)])
plt.autoscale(tight=True)
plt.grid(True, linestyle='-', color = '0.75')
plt.show()
plt.plot(fx,fa1(fx),linewidth=4)
plt.plot(fx,fb1(fx),linewidth=4)
plt.legend(["d = %i" % fa1.order,"d = %i" % fb1.order], loc = "upper left")
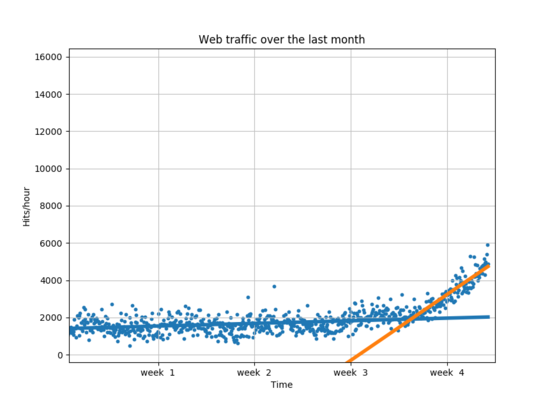
위의 결과로 봤을 때 두 직선은 이전의 모델들 보다 데이터에 매우 잘 적합한 것으로 보이지만 고차원일때의 오차보다 큰 편이다.
하지만 이전의 모델들 보다 마지막 주에 적합하게 만든 모형을 더 신용하는 것은 직선형 모델일 수록 미래를 예측하는데 좀 더 적합하다고 생각할 수 있기 때문이다.
해당 부분은 같이 첨부한 ml_analyze_webstats.py를 실행하며 Python3로 실행해주기 바란다.
ml_analyze_webstats.py는 기존의 리눅스 환경에서 실행될 코드(analyze_webstats.py)를 윈도우+파이참 환경에 적용하면서 변형시킨 코드임을 참고하기 바란다.
결과를 비교하고 싶은 사람들을 위해 chart.zip 파일에 실행결과를 넣어 두었다. SciPy의 optimize 모듈의 fsolve 함수를 사용해서 다항식의 근을 찾을 수 있다.
예시에서는 100,000 hits/hour 이고 그 때는 9.616071 주차 이므로 9~10주차 사이임을 알 수 있다.


댓글남기기