[Python Deep Learning] 6. 최적화

1. 최적화 (Opmization)

일반적인 딥러닝 모델은 크기가 큰 데이터의 경우에는 잘 작동하지만, 훈련 속도 측면에서는 느려진다. 이에 대해 이번 장에서는 신경망을 얼마나 빠르게 학습시키는 가와 관련해서 최적화 알고리즘에 대해 살펴보자. 이번 장에서 다룰 내용들은 대략적으로 아래 그림과 같이 나타낼 수 있다.

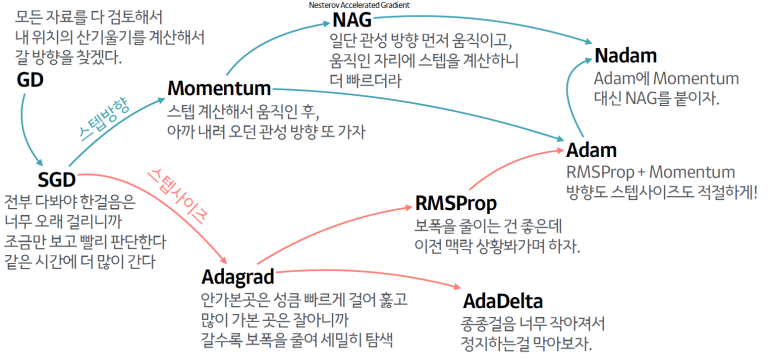
2. 경사하강법

앞선 장에서도 설명했기에 간단하게만 짚고 넘어가자. 경사하강법이란 손실함수의 최소화 되는 지점을 찾기 위해서 사용된 파라미터의 기울기가 줄어드는 방향으로 가중치를 최적화하는 기법이다. 종류로는 임의의 데이터 1개만 사용하여 에러를 구하고, 기울기를 계산하는 Stochastic GD, 반대로 전체 데이터 셋에 대한 에러를 구한 후 기울기를 한 번만 계산해 모델의 파라미터를 업데이트하는 Batch GD, 그리고 Stochastic 과 Batch 의 중간 과정으로 전체 데이터 중 일부만을 추출해 각 데이터에 대한 기울기를 계산한 후, 이를 평균 기울기로 모델의 파라미터를 업데이트 하는 Mini-Batch GD 가 있다.
하지만 경사하강법의 경우, Saddle Point 혹은 Local Minima 문제에 빠질 수 있다는 단점이 있으며, 별다른 규제가 없다면, 학습이 원할하지 않아, 그레디언트가 소실되거나, 발산하는 문제도 발생하게 된다.

3. 모멘텀 (Momentum)

위의 내용과 같이 경사하강법에서 발생하는 문제를 해결하기 위해서 사용된 알고리즘이며, 관성의 법칙과도 연관이 있다. 모멘텀, 즉 관성이란, 물체에 작용하는 힘의 총합이 0일 때, 현재 운동상태를 유지하려는 현상을 의미한다.
즉, 내가 이동했던 방향으로 관성을 갖고 경사하강법을 수행하는 것이 모멘텀 알고리즘의 특징이다. 이를 수식으로 표현하면 다음과 같다.

$ v_t = {\gamma }v_{t-1} + {\eta }{\nabla }_{\theta } J({\theta }) $

$ \theta_t = \theta_{t-1} - v_t $

경사하강법을 계산한 수식과 비교하면, 이전 결과부분에 감마(γ) 가 곱해졌다는 점이 차이인데, 이는 이전 그레디언트의 비중을 추가해 줌으로써, 관성을 갖도록 하기 위한 장치라고 볼 수 있다.
아래 그림은 기존의 경사하강법을 이용했을 때 최적화 진행 과정과 모멘텀을 이용했을 때 최적화 진행과정을 비교한 것이다.

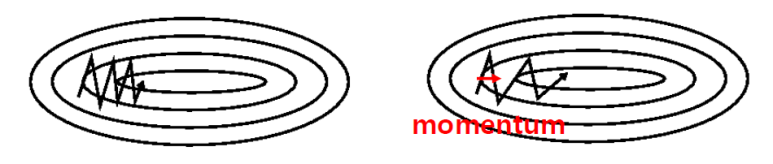
왼쪽이 기존의 경사하강법을 사용한 결과인데, 모멘텀은 기존 결과에 비해 좀 더 큰 폭으로 중앙(최적점)에 도달할 수 있다. 하지만, 진자의 운동처럼, 한 번에 최적점에 도달하는 것이 아니라 조금 지나쳤다가 점차적으로 최적점에 도달하게 된다.

4. NAG (Nesterov Accelerated Gradient)

방금 전에 본 모멘텀은 경사하강법 보다는 빠르게 학습할 수 있다는 장점이 있지만, 최적점을 지나치고 진자운동을 통해 최적점에 도달하는 데에는 다소 오래 걸릴 수도 있다는 단점이 있다. 때문에 이를 개선하기 위한 모델이 NAG 이다.
NAG는 기존 경사하강법, 모멘텀의 기법과는 달리, 먼저 관성을 방향으로 이동한 뒤에 그레디언트를 계산한다. 이것이 어떤 차이를 만드는 지는 아래 그림과 함께 설명하겠다.

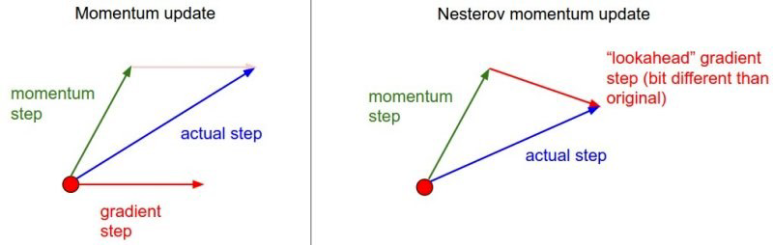
일반적으로 경사하강법이나, 모멘텀은 이전 위치에서 그레디언트를 계산했고, 계산 결과와 관성방향에 대해 내적방향으로 이동했었다. 하지만, NAG는 순서를 바꿔서, 관성의 방향(momentum step)으로 먼저 이동을 하고, 해당 위치에서 그레디언트를 계산해서 위치를 찾는다. 이후 이전 결과에서 도출된 위치까지 이동하는 방식으로 동작한다.
그 결과 위의 그림에서처럼, NAG로 최적화 했을 때의 이동하는 거리가 모멘텀을 사용했을 때보다 더 짧은 거리로 이동한다는 것을 확인할 수 있으며, 이는 그만큼 최적점을 지나치는 거리가 짧아지기 때문에, 모멘텀보다는 좀 더 빠르게 학습을 완료할 수 있다는 말과 이어진다. 위의 내용을 수식으로 표현하면, 다음과 같다.

$ v_t = \gamma v_{t-1} + \eta \nabla_{\theta} J(\theta - \gamma v_{t-1}) $

$ \theta_t = \theta_{t-1} - v_t $

5. AdaGrad (Adaptive Gradient Descent)

이전까지 살펴본 모멘텀, NAG는 그레디언트의 진행 방향에 대한 이야기들이었고, 지금부터 다룰 최적화 기법들은 그레디언트가 이동하는 폭에 대한 이야기이다.
가장 먼저 만나볼 기법은 AdaGrad 인데, 이 기법이 등장하게 된 배경은 학습률의 감소와 연관이 있다. 이전 장에서 설명했듯이, 학습률이 너무 적으면 학습 시간이 너무 길어지고, 반대로 학습률이 너무 크면, 발산하게 되서 학습이 제대로 이뤄지지 않는다. 이를 위해 수행되는 것이 학습률 감소라는 방법이다.
AdaGrad 는 개별 매개 변수에 적응적으로(adaptive) 학습률을 조정하면서 학습을 진행한다. 이해를 돕기위해 아래와 같이 w1 과 w2 인 노드가 있다고 가정해보자.

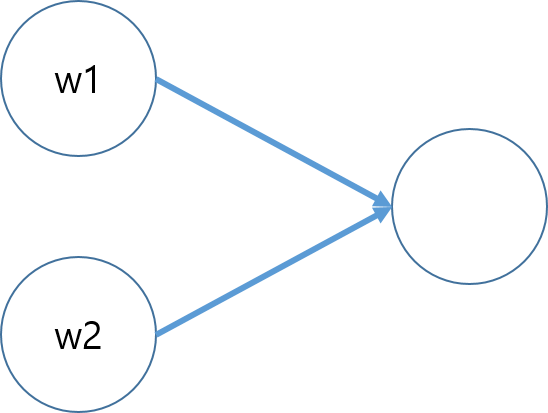
만약 w1 에 비해 w2 가 더 빠르게 최적값에 도달하는 경우라면, 학습을 중지해야되지만, w1 의 학습이 원할하지 않으면, 그레디언트가 크게 증가하고, 학습률도 2개 노드 모두 공유하는 상황이기 때문에 학습속도가 느려진다는 단점이 있다. 그렇다면 AdaGrad 는 어떻게 조정할 수 있을까? 갱신 방법을 수식을 표현하면 아래와 같다.

$ G_t = G_{t-1} + {(\nabla_{\theta} J(\theta_t))}^2 $

$ \theta_{t+1} = \theta_t - \frac {\eta } {\sqrt {G_t + \epsilon } } \cdot \nabla_{\theta} J(\theta_t) $

다소 복잡해보이지만, 위의 수식 내용을 해석해보면 다음과 같다.
먼저, 등장하는 변수들부터 정리해보면, θ 는 갱신할 가중치 매개 변수, ∇θJ(θt) 는 W에 대한 손실함수 기울기, η 는 학습률이다. 추가적으로 위 식에 등장하는 Gt 는 기존 기울기 값을 행렬곱해서 나온 결과이며, 이는 가중치 갱신할 때, 학습률을 조정해주는 역할 로 사용된다. 즉, 매개변수들의 원소 중에서 가장 많이 움직인(갱신이 크게 된) 요소의 경우에는 학습률을 낮춘다는 것이고, 이는 학습률 감소가 매개변수의 원소마다 다르게 적용시킨다는 말이다. 이 말은 신경망으로 구성하는 각 노드 별로 학습률이 각각 적용된다는 것이다. 이로 인해 앞서 예시로 든 w1 과 w2 가 서로 최적값에 도달하는 시간이 다르더라도, 학습률을 다르게 설정할 수 있기 때문에 모델 전체적인 학습속도는 이전보다 오를 것이다.
하지만, AdaGrad 도 단점은 있다. 위의 수식을 살펴보면, 변수 h 는 앞서 언급한 것처럼 과거의 기울기를 행렬곱으로 곱하고 이를 계속 더해간다. 때문에 학습이 오래 진행될 수록 갱신되는 정도가 약해지게 되며, 무한히 학습을 하게되면, 어느 순간 갱신량이 0이 되는, Gradient Vanishing 이 발생한다.

6. RMSProp

위에서 본 AdaGrad의 단점을 해결하기 위해서 개발된 기법이다. 동작 과정은 AdaGrad 기법과 유사하지만, 그레디언트가 이동할 때, 이동 비중을 곱해 줌으로써 기울기를 단순 누적하는 것이 아니라 지수 가중 이동 평균(Exponentially Weighted moving average)으로 더 크게 반영하도록 한다. 수식으로는 아래와 같다.

$ G_t = \gamma G_{t-1} + (1 - \gamma ){(\nabla_{\theta} J(\theta_t))}^2 $

$ \theta_{t+1} = \theta_t - \frac {\eta } {\sqrt {G_t + \epsilon} }\nabla_{\theta} J(\theta_t) $

위의 수식들을 잘 보면 낯익은 부분들이 있다. 그레디언트 계산하는 부분은 위에서 등장했던 모멘텀과 유사하다는 것을 알 수있다. 즉, 그레디언트를 계산할 때 가중치에 대한 비중(Moving Rate)을 그레디언트를 계산할 때 반영함으로써, 가중치를 반영할 때 더 크게 반영될 수 있도록 해준다.

7. Adam(Adaptive Moment Estimation)

Adam 알고리즘은 간단하게 말해서, 모멘텀의 장점과 RMSProp 을 장점만을 가져와 결합한 결과물이라고 할 수 있다. 즉, 이동 방향은 모멘텀 처럼 관성을 가진 채로 이동하고, 학습률을 조정하는 방법은 RMSProp 처럼 신경망을 구성하는 각각의 노드별로 가중치를 부여하겠다는 의미이다. 식으로 표현하면 아래와 같다.

$ m_t = \beta_1 m_{t-1} + (1 - \beta_1)g_t $

$v_t = \beta_2 v_{t-1} + (1 - \beta_2)g_t^2 $

위의 수식에서 $ \beta $ 값은 Bias Correction Term 이라고 해서 편향을 조정하기 위한 값이라고 보면 된다.

8. 정리하며

지금까지 7개정도의 최적화 기법들을 살펴봤다. 위에서 살펴본 기법들 외에도 여러가지 기법들이 있으며, 궁금한 사람은 최적화 기법과 관련해서 조사해보기 바란다. 마지막으로 앞서 본 기법들의 학습 속도를 전체적으로 비교해보자.

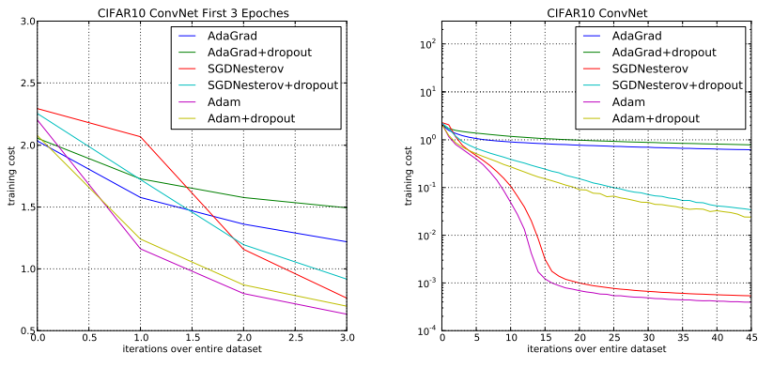
위의 그래프는 데이터 셋의 크기별로 소요된 학습 비용을 표시한 것이다. 때문에 학습비용이 덜 들어갈 수록 최적화가 잘 되고, 학습 속도가 빠르다라고 이해하면 되며, 그래프 상으론 Adam 기법을 사용하는 것이 가장 좋다고 볼 수 있다.