[Python Deep Learning] 5. 신경망의 학습

1. 신경망의 종류

신경망은 은닉층의 갯수에 따라 크게 얕은 신경망과 깊은 신경망으로 나뉘게 된다고 1장에서 언급한 적이 있다. 현재까지 다뤘던 예제들의 경우 대부분이 은닉층이 2개 이하였던 얕은 신경망에 대해서 다뤄봤다. 때문에 이번 장을 시작으로 깊은 신경망에 대해서 다룰 예정이며, 그 전에 지금까지 이야기 했던 신경망에 대한 기초적인 내용들과 다루지 않았던 내용들을 다루고자 한다. 앝은 신경망이 은닉층 2개 이하의 신경망이였다면, 깊은 신경망은 아래 그림과 같이 구조상으로 은닉층이 3개 이상인 경우가 해당된다.

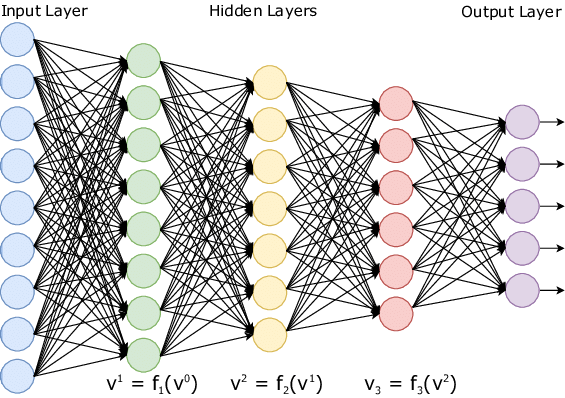
입력층으로부터 입력을 받아 좀 더 복잡해진 은닉층에서 활성화 함수를 통해 계산된 결과를 다음 층으로 전달되며, 최종 출력층에서는 손실함수를 통해 결과가 도출된다.
그렇다면, 앝은 신경망일 때와 달라진 점은 어떤 것이 있을까? 우선 은닉층의 수가 많아졌고, 이에 따라 비선형적으로 변환되는 일이 발생한다. 뿐만 아니라 학습의 매개 변수 수가 계층이 많을수록 계층 크기의 제곱에 비례하는 성형이 있다. 마지막으로 신경망이 깊어짐에 따라 그레디언트가 소실되는 등 기존 얕은 신경망을 사용했을 때는 드러나지 않았던 문제들이 나오게 된다. 관련된 문제들과 문제에 대한 해결법 역시 이번 장에 다룰 예정이다.

2. 학습 시 고려해야되는 사항들

신경망의 학습과정은 이전 장이였던 경사하강법 부분에서 설명을 했기에, 대신 이번 장에서는 신경망의 학습과정에서 고려해야되는 사항들을 살펴보자.

1) 가중치 초기화 (Weight Initialization)

위의 내용을 보고 가장 먼저 드는 의문은 가중치는 어떻게 초기화가 될까이다. 최초에는 특정 범위 내에서 임의의 값을 추출해서 사용했다. 임의의 값으로 사용하게 된 계기는 가중치의 값이 모두 같은 경우 하나의 클래스에 대해서 가중치 전체가 동시에 같은 값으로 업데이트될 것이다. 이는 노드의 가중치별로 차별성을 둬야되는 데, 그것이 사라지게 되는 것과 같아서 결과적으론 학습이 원할하지 않게 된다.
하지만 임의의 값으로 부여하는 것에도 문제가 있었다. 만약 설정된 값이 전부 0에 수렴할 정도로 가까운 값들로 구성된다면 어떨까?
가중치가 업데이트될 때는 일반적으로 정규분포를 만들기 위해 0 ~ 1 사이의 값으로 설정하게 되는데, 0에 가까운 값에 0에 가까울 만큼 작은 값을 곱하면, 결과적으로 더욱 0에 가까워지게된다. 그리고 이러한 현상이 반복되면 그레디언트가 소실되는 “Gradient Vanishing” 현상이 발생한다. 위와 같은 문제를 해결하기 위해 가중치 초기화에는 총 2가지의 방법이 있다.

(1) 자비에르 초기화(Xavier Initialization)

단순히 0에 가까운 임의의 값을 사용하는 것이 아니라, 연결된 노드 개수를 고려해서 가중치를 초기화하는 방법이다. 초기 값은 임의의 가중치를 설정하되, 설정된 값은 노드 개수의 제곱근한 값으로 설정한다. 가령 전체 노드 개수가 16개인 경우에는 “ 초기화 값 = 설정값 / 4” 으로 설정한다는 의미이다. 단, 사용을 위해서는 활성화 함수가 선형함수여야 하고, 입력과 출력의 분산이 같다고 가정해야한다.
활성화함수는 뒤에서 나오겠지만, 자비에르 초기화는 비선형성이라는 특징이 있어 사용되는 것인데, 결과가 선형으로 나오면 의미가 없어지기 때문이다.

(2) He 초기화(He Initialization)

앞서 본 자비에르 초기화는 활성화 함수가 비선형함수여야만 한다는 단점을 해결하기 위해 만들어진 초기화 방법론이며, 활성화함수에 관계없이, 분산을 같게 보자는 것이 목적이다.

2) 활성화 함수(Activation Function)

그렇다면, 활성화 함수는 무엇일지 알아보자. 활성화 함수(Activation Function)은 노드로 들어오는 입력값에 대해 출력의 결과가 비선형성을 갖도록 만들어주는 함수이며, 비선형성을 만들어야하기 때문에, 활성화 함수로 사용되는 함수들은 모두 비선형 함수의 형태를 갖는다.
이에 대해 선형 함수를 썼을 때 어떤 문제가 있었을까에 대한 의문이 생긴다. 이와 관련된 답은 퍼셉트론과 연관이 있다. 인공신경망이 생성되기 전, 회귀와 분류문제 모두에 대해서 퍼셉트론이 사용될 만큼 성능이 우수했었다. 당시에 주어진 문제들이 모두 선형함수를 이용해서 분류가 가능했고, 회귀에 대한 예측도 가능했기 때문이다. 하지만, XOR 를 분류하는 문제에서 퍼셉트론이 분류하지 못하는 현상이 발생한다. 이 문제를 해결하기 위해서 등장한 것이 앞선 예제에서 봤던 Sigmoid 함수이다. 다른 말로는 Logistic 함수라고도 불리는 이 함수는 선형 구조인 다층 퍼셉트론에서 비선형 값을 얻어내기 위해 사용되었다. 이를 계기로 활성화 함수는 선형이 아닌 비선형함수들, 특히 Sigmoid 계열의 함수를 사용했다.

(1) 시그모이드 계열 함수

활성화 함수는 크게 2가지 계열이 많이 사용되었는데, 하나는 방금 전에 나온 Sigmoid 계열이고, 다른 하나는 ReLU 계열이다. Sigmoid 계열의 함수들은 그래프로 나타냈을 때 형태가 S 자 형태를 띄고, 특정 범위 내에서만 값을 나타내며, 특정 지점을 기준으로 분류할 수 있다는 장점이 있다.
때문에 활성화 함수를 비선형함수로 바꿨을 때 많이 사용된 함수 계열이지만, 여기에도 심각한 문제점들이 있다.

• Gradient Vanishing 시그모이드 게열 함수의 특성 상 분모에 1+ ex 와 같이 큰 값이 존재한다. 때문에 x 에 들어오는 입력 값의 크기가 클 수록 더욱 0에 가까워지개 되며, 특정 입력 값 이상의 수치에 대해서는 그레디언트가 소실되는 문제가 발생한다.
  

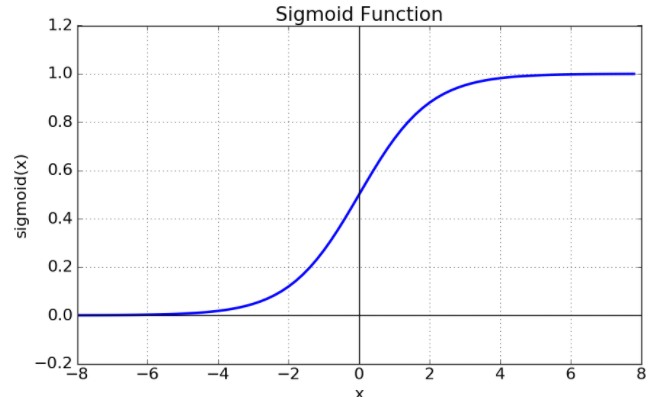
• 0 에 근사한 값으로 수렴하기 때문에 완벽하게 0이 출력되지 않는다. 위의 함수 형태를 보면, 어떤 구간에서는 양수가 나올 수 있고, 어떤 구간에서는 음수가 나올 수 있다. 때문에 활성화 함수의 결과값인 f(wx + b) 가 양수일 수도, 음수일 수도 있기 때문에 그래프로 표현하게 되면, 아래 그림과 같이 나타날 수 있게 된다.
  

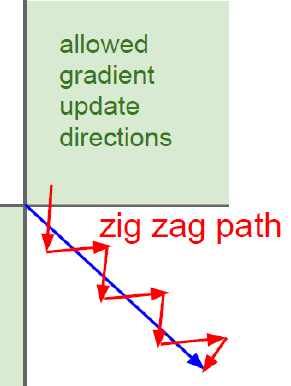
• 지수의 거듭제곱으로 계산되기 때문에 연산량이 많아져 학습 속도가 느려진다. 시그모이드 함수의 수식으로 보면 알 수 있듯이, 지수의 거듭제곱 형태가 존재하기 때문에 숫자가 커질 수록 그에 대한 연산량도 많아지게 된다.
  

(2) ReLU(Rectified Linear Unit) 계열 함수

위와 같은 문제가 발생해서 ReLU 함수를 사용하게 된 것이다. ReLU 계열의 함수는 아래 그래프에서처럼 입력값이 양수인 구간에서의 출력값은 양수를, 0 이하인 경우에는 0을 출력하는 비선형 함수다.

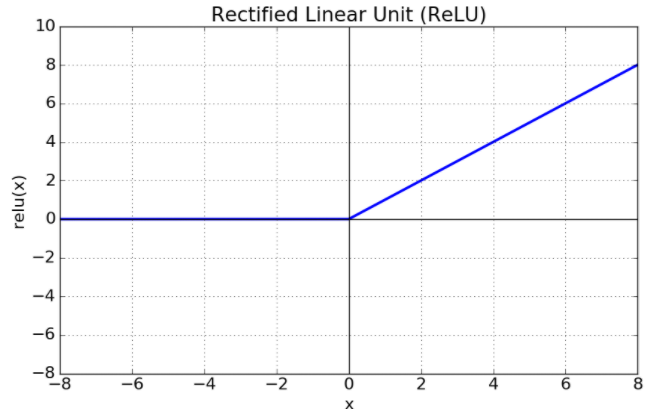
특징으로는 입력값이 양수인 부분에서만 계산하면 되기 때문에, 시그모이드 계열의 함수들보다는 계산 속도가 빠르고, 그만큼 연산 비용이 들지 않으며, 구현도 간단하다. 하지만, 음수인 값에 대해서는 출력이 0이기 때문에 뉴런이 죽을 수도 있다는 단점이 존재한다. 이러한 단점을 해결하기 위해, Leaky ReLU, PReLU 등의 함수들이 추가적으로 생성되었다.

(3) SoftMax 함수

앞서 본 시그모이드 계열이나 ReLU 계열이나 모두 이진분류에서는 확실히 효과를 보였다. 하지만, 다중 분류 문제에서는 어떨까? 만약 시그모이드 계열이나 ReLU 계열을 사용한다라고 하면 불가능했을 것이다. 만약 가능하다해도, 이진분류된 것을 다시 각각 이진분류를 하는 등 계산에 대한 비용이 많이 들었을 것이다. 이런 문제를 해결하기 위한 함수 중 대표적인 예시로 SoftMax 함수가 있다.
SoftMax 함수는 입력 받은 값을 0 ~ 1 사이의 값으로 출력해주며, 모두 정규화하여 출력 결과의 총합이 1이 되도록 하는 함수이다. 출력되는 값의 개수는 분류하려는 클래스의 개수와 동일하다.
다중분류 문제의 경우 SoftMax 함수에 One-Hot Encoding 을 같이 사용하는 경우가 많은데, One-Hot Encoding 이란, 정답인 인덱스에 해당하는 부분만 1로 표기하고, 나머지는 0으로 채워주는 벡터 표현법을 의미한다.

3) Learning Rate Tunning

(1) 학습률(Learning Rate)

앞서 경사하강법에서도 언급했던 것처럼 학습률이라 함은, 현재 위치에서 다음 위치로 얼마만큼 이동할지, 얼마만큼 세세하게 학습을 하는지를 결정하는 요소다. 그만큼 학습에 대한 속도와 오차발생과도 연관이 있는 중요한 요소라고 할 수 있다.

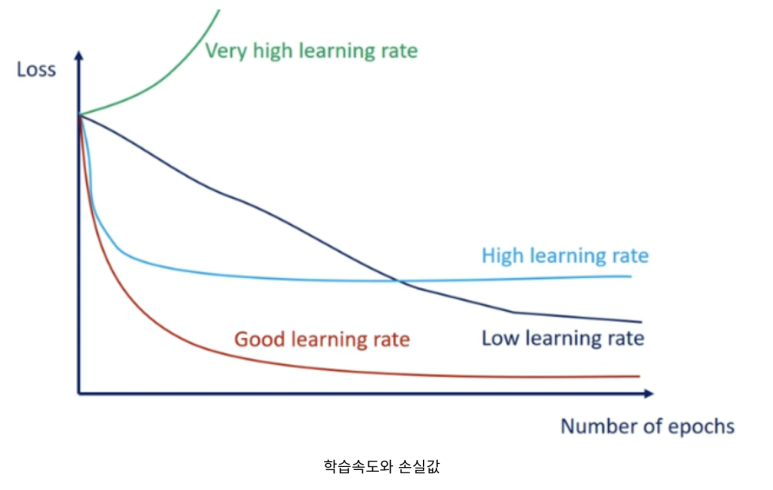
만약 학습률을 크게 설정하면, 최적값을 지나쳐 발산하게되는 경우가 발생할 수 있으며, 반대로 너무 작은 값으로 설정하게되면, 학습의 속도가 너무 느리거나, 지역 최소값에 빠지는 문제(Local Minima)가 발생할 수 있다.

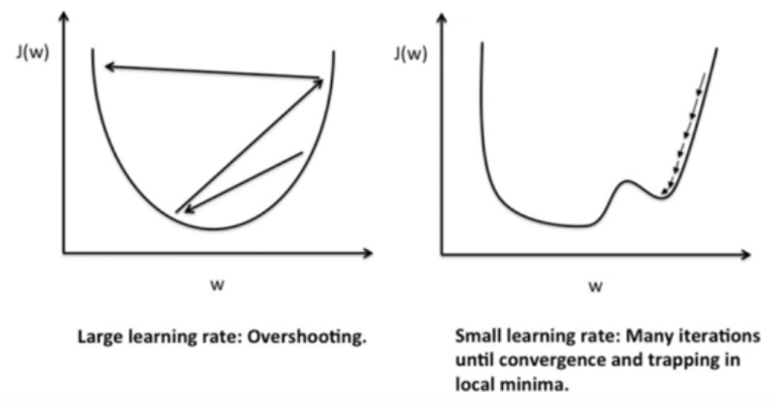
때문에 적절한 학습률을 찾기 위해서는 여러 값을 직접 대입해보는 방법이 가장 좋은데, 이와 관련하여 어떻게 설정하면 좋을지, 크게 3가지 방법에 대해서 살펴볼 예정이다.

(2) Learning Rate Decay

먼저 알아볼 방법은 Learning Rate Decay 이다. 앞서 언급한 데로, 학습률을 너무 크게 하면 발산을, 너무 작으면 제 시간에 학습을 못하거나, 지역 최소값에 빠질 수 있다. 이를 방지하기 위해서, 학습 초기에는 큰 폭으로 움직이다가 일정 조건이 되면, 점차적으로 보폭을 줄이는 방법이다.

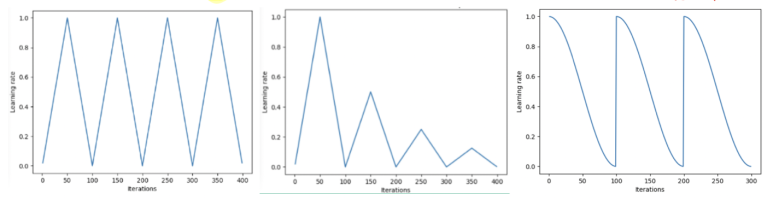
위의 그림에서처럼 특정 조건을 만족할 때마다 학습률이 급속하게 감소하는 것을 볼 수 있으며, 학습이 진행됨에 따라 학습률이 조금씩 감소하는 것도 확인할 수 있다.
하지만, 이 방법의 경우 최적 값을 금방 찾을 수 있지만, 지역 최소값이 포함되거나 saddle point 와 같은 부분이 존재할 때, 학습률이 낮은 상태에서 직면하면, 탈출하지 못한다는 단점이 있다.

(3) Cyclic Learning Rate

Learning Rate Decay 로는 saddle point 를 포함한 지역최소값에서 학습률 마저 작은 상태라면 탈출하지 못한다는 단점을 극복하기 위해서 등장한 방법이다. 극복하기 위한 방법은 학습률을 주기적으로 변경해보자는 의견이다. 이러한 방법은 지역 최소값을 만나게 되면 학습률을 키워서 빠져나갈수 있다는 장점이 있지만, Learning Rate Decay 보다 최적 값을 찾는 시간은 늦어질 수 있다는 단점이 있다.

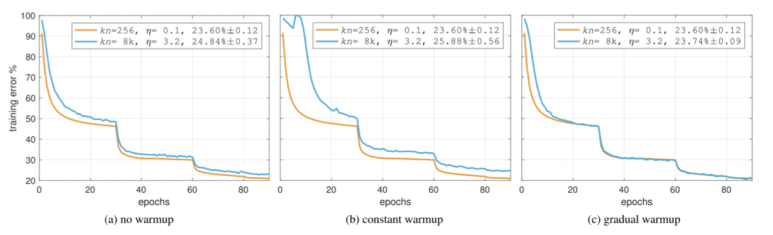
(4) Warm-up

이번에는 Warm up 에 대해서 알아보자. 흔히 웜 업(warm up) 이라고 하면, 운동을 하기 전에 몸을 풀어주기 위한 준비운동을 말한다. 이와 유사하게 모델의 학습을 위해 학습률을 선형적으로 증가시켰다가 일정 수준이 되면, 조금씩 줄이는 방법이다.

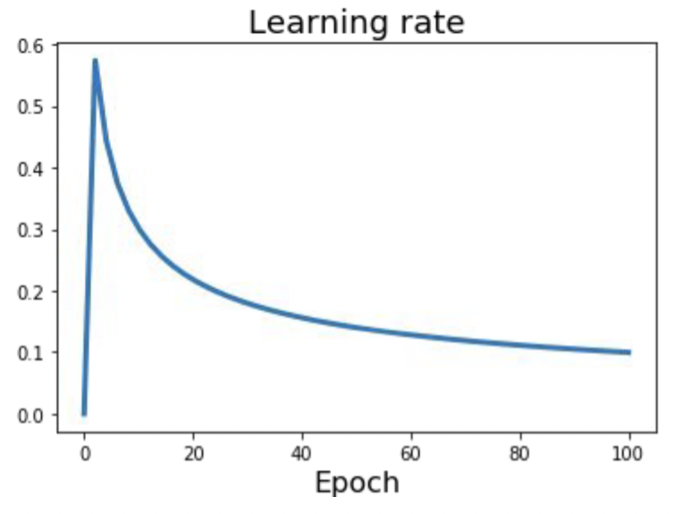
이를 Linear Warm Up 이라고 부른다. 학습 초기에 학습률이 선형적으로 증가하는 모습을 보고 붙여진 이름이다. 위의 그림처럼 학습률이 특정 값까지 도달하게되면, 이후부터 점점 낮아지는 현상으로 보이며, 일정 학습시간 후부터는 수렴하는 현상을 볼 수 있다.

4) 딥러닝을 어렵게 만드는 것

이번에는 딥러닝 학습 시, 이를 어렵게 만드는 요소들을 살펴보자. 크게 아래와 같이 3가지의 문제점이 존재한다.

(1) Vanishing Gradient

앞서 ReLU 계열의 함수를 사용하기 이전에는 시그모이드 계열의 함수를 사용했다고 언급했었다. 분류 문제등에서 물론 잘 동작하였지만, 치명적인 문제점이 하나 있었다. 바로 시그모이드 계열 함수를 활성화함수로 사용하고, 그레디언트를 계산할 때, 계산된 그레디언트의 값이 너무 작아져서 나중에서는 0에 근사하는, 소멸되어버리는 것이다.
아래 그림에서처럼 output 방향에서 input 방향으로 역전파를 수행할 때, 그레디언트를 거듭 곱하게 되기 때문에, 점점 0에 근사한 값이 생성되고, input 에 도달했을 때는 가중치가 0이 되어 없어진것처럼 보이게 된다.

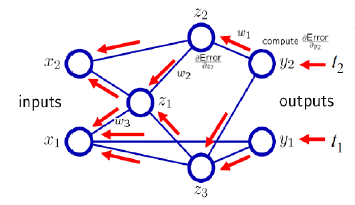
(2) Underfitting vs. Overfitting

우선 신경망의 목적은 처음 보는 데이터에 대해서도 예측하는 것이 목적이며, 그에 대한 오차를 줄이는 것이 목적이다. 여기서 말하는 오차란, 학습오차(Trainning Error) 와 일반화 오차(Generation Gap) 의 합을 의미하며, 결과적으로 신경망의 목적은 이 두가지 모두를 최소화하는 것이 목적이라고 할 수 있다.

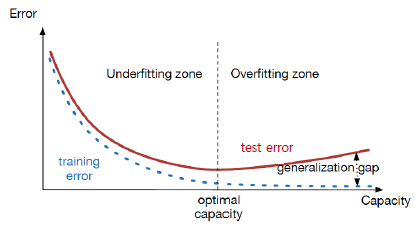
이 중 일반화 오차는 모델의 학습파라미터 수(model capacity)와 관련이 있는데, 만약 모델의 파라미터 수가 너무 작으면, 아무리 학습을 해도 성능이 나오지 않을 것이다. 이를 과소적합(Underfitting) 이라고 부른다. 반면 모델의 파라미터 수가 너무 많으면, 일반화 오차가 커지게 되며, 모델이 데이터에 의존하는 성향으로 보인다. 이를 과대적합(Overfitting)이라고 부른다.

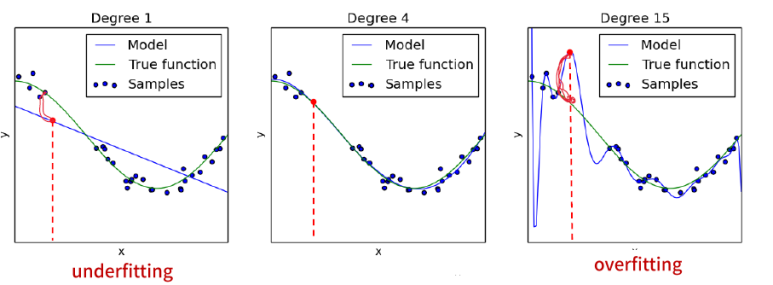
일반적으로 딥러닝에서 사용되는 모델들은 학습 파라미터 수가 많은 편에 속하기 때문에 과대적합에 노출될 가능성이 높다. 이를 어떻게 해결하는 지에 대해서 살펴보도록 하자.

(3) Stuck in Local Minima

학습 시, 에러를 최소화해주는 파라미터를 찾는 과정에서 아래 그림처럼, 지역 최소값에 갇혀서 움직임 없이 종료하는 문제를 가리켜 Stuck in Local Minima 라고 표현한다.

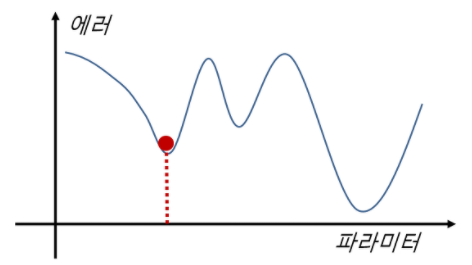
이처럼 지역 최소값에 빠지게 되는 이유는 앞서 신경망은 학습 시, 경사하강법을 사용해 학습을 한다고 했다. 이 때 학습의 속도를 결정짓는 것은 학습률인데, 학습률을 너무 크게 설정하면, 전역 최소값을 지나칠 수 있고, 반대로 너무 작게 설정하면 학습속도가 느려져 지역 최소값에 빠지게 된다.

5) 해결 방법

그렇다면 위의 문제들을 어떤 식으로 해결할 수 있을 지 하나씩 살펴보자.

(1) Early Stopping

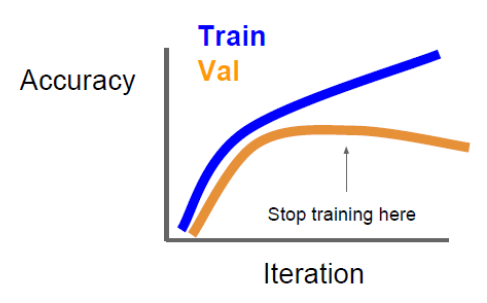
일반적으로 딥러닝에 사용되는 신경망을 학습시키기 위해서는 학습을 많이 해야되며, 이에 따라 Epoch 수도 크다. 하지만, 너무 커지면 Overfitting이 발생할 수 있으며, Overfitting을 피하기 위해 Epoch 수를 줄인다해도 너무 줄이면, 오히려 Underfitting 이 발생할 수 있다.
이를 위해 학습 시, 학습 정확도와 모델 검증 정확도를 비교해, 검증 정확도가 떨어지는 시점에서 학습을 종료하는 방법이다.

텐서플로에서 Earlystopping 을 설정하려면 아래와 같이 코드를 작성하면 된다.

[Python Code]

import tensorflow as tf
from tensorflow import keras

early_stopping = keras.callbacks.EarlyStopping(monitor='val_loss', patience=100)

hist = model.fit(
    x_train, y_train,
    epochs=10, batch_size=10,
    callbacks=[early_stopping]
)

(2) 규제 (Regularization)

또다른 방법으로는 모델에 제약을 줘서, 모델의 손실이 최대한 0에 근사한 값이 나올 수 있도록 하는 방법이다.
이 때 제약이 가해지는 대상은 가중치이다. 가중치를 최적화 하기 위해서는 해당 값이 최소화 항목이 되는 것이 좋다. 방법을 확인하기 전에, 먼저 손실함수에 대해서 수식적으로 살펴보자.

$ L(W) = \frac {1} {N} \sum _{i=1}^N L_i(f(x_i, W), y_i)$

다음으로는 규제를 하게 되면 어떻게 수식으로 표현할 지를 알아보자.

$ L(W) = \frac {1} {N} \sum _{i=1}^N L_i(f(x_i, W), y_i) + \lambda R(W) $

위의 식과 다른 점은 규제를 적용한 부분이 추가 되었으며, 이는 손실에 가중치 규제를 최소화 시킴으로써, 가중치가 커지지 못하게 하여, 결과적으로는 과적합을 방지할 수 있다.
규제를 하는 방법은 크게 L1, L2 규제방법이 존재하며, 이는 머신러닝 중 회귀 부분에서 다뤘기 때문에 이번장에서는 넘어가기로 하자. 궁금한 사람은 머신러닝 회귀 부분을 확인하고 오기 바란다.

[Python Machine Learning] 2. 회귀

(3) 드롭아웃 (Dropout)

앞서 살펴본 정규화 혹은 규제와 관련된 기법 중 하나로, 학습 회차 마다 일정한 확률로 임의의 노드만 선택해서 학습과정에서 제외하고 학습하는 방법으로, 주로 신경망의 구조가 복잡해지면 가중치의 감소 만으로 조절하기 어려워지기 때문에, 드롭아웃 기법을 통해 과적합에 좀 더 내성이 있는 모델을 생성하기 위함이다.
물론 학습 과정에서 임의의 뉴런을 배제하고 학습하는 것이며, 실제 예측을 하는 과정에서는 신경망을 구성하는 모든 노드를 활용해서 사용한다.

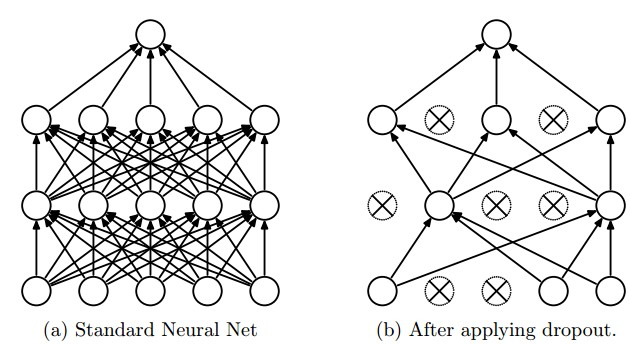
위의 그림에서처럼 x 가 없는 노드들만 학습에 사용하며, 이와 같은 과정을 반복하게 되면서 과적합에 내성이 생기는 것이다. 또한 학습마다 사용되는 노드들과 파라미터 값이 바뀌기 때문에, 앙상블 기법의 일종으로 보기도 한다.

(4) 배치 정규화 (Batch Normalization)

우선 배치 정규화를 설명하기 전에, 연관된 문제점인 화이트닝(Whitening) 에 대해서 알아보자. 화이트닝이란, 소위 백색잡음이라는 말로 많이 쓰이는데, 각 레이어별로 입력의 분산을 평균 0, 표준편차가 1인 입력값으로 정규화 시키는 방법이다. 이는 기본적으로 들어오는 입력값 및 특징들간에 상호연관성이 없도록 해주며, 각각 분산을 1로 만을어 주는 효과가 있다. 하지만, 계산량이 많을 뿐만 아니라, 일부 파라미터들의 영향은 무시되는 단점이 존재한다. 이를 해결하기 위한 방법 중 하나가 지금부터 살펴볼 배치 정규화다.
배치 정규화는 평균과 분산을 조정하는 과정이, 신경망안에 포함되어 학습 시 평균과 분산을 조절이 같이 된다. 즉, 각 레이어마다 정규화하는 레이어를 둬서, 변형된 분포가 나오지 않도록 조절하는 방법이라고 이해하면 된다.
방법은 미니배치의 평균과 분산을 이용해 정규화를 하게 되는데, 여기서 사용되는 변수들은 모두 학습 가능한 변수이며, 역전파를 통해서 학습이 진행된다.

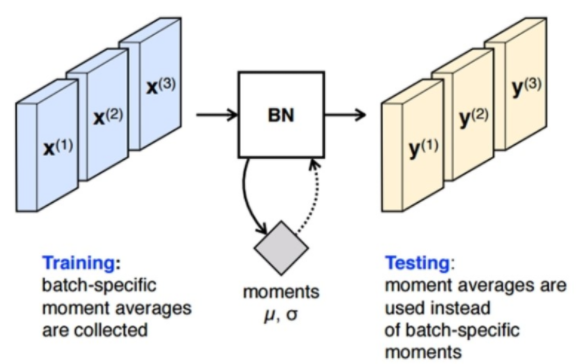
배치 정규화를 적용하게 되면, 먼저 단순하게 평균과 분산을 구하는 것이 아니라 감마, 베타를 통한 변환이 적용되므로 비선형 성질을 유지하면서 학습을 할 수 있다. 학습 시에 신경망 레이어의 중간에 위치하여 학습을 통해 관련 변수를 계산할 수 있다.
두번째로는 학습률(Learning Rate) 값을 높게 설정해도 이상이 없다는 점이다. 기존에는 학습률을 높게 잡을 경우 그레디언트가 소실되거나, 발산하거나 혹은 Local Minima 와 같이 지역 최솟값에 갇힐 우려가 있었지만, 배치정규화는 파라미터의 scale 에 영향을 받지 않기 때문에, 위의 문제들을 걱정할 필요가 없다.
마지막 효과로는 규제의 일종이 되기도 한다. 앞서 살펴본 다른 기법들을 보면, 일반적으로 평균과 분산을 바꿔주기 위해 랜덤하게 선택된다거나 하는 식으로 랜덤성을 충족해야되는데, 배치를 핼 때 랜덤하게 선택되기 때문에 규제의 효과도 갖는다고 할 수 있다.
방금 언급했듯이, 드롭아웃처럼 랜덤성이 존재하기 때문에 학습 시에만 사용되어야하며, 테스트 단계에서는 제거를 하고 수행해야한다.

[참고자료]
https://eehoeskrap.tistory.com/430