[Python Deep Learning] 4. 경사하강법 (Gradient Descent)

1. 신경망의 학습과정
경사하강법이 어떻게 신경망과 연관이 있는지 알아보기 위해 간단하게 신경망의 학습과정을 살펴보자. 신경망은 아래 그림에서처럼 총 2단계로 나눠서 학습이 진행된다. 먼저 예측값을 계산하는 과정인 순방향 전파(Feed-Forward) 라고 부르는 과정과, 실제값과 예측결과의 비교를 통해 오차를 계산하고, 적절한 가중치를 수정하는 과정인 역방향 전파(Back-Propagation)이다.
1) 순방향 전파(Feed Forward)
순방향 전파는 신경망이 실행하는 시작부분부터 최종 결과가 산출되는 부분까지의 과정이다. 신경망을 실행하게되면 가장 먼저 실행되는 부분은 초기 가중치(Weight) 및 편향(Bias)에 대한 설정이다. 가중치는 입력되는 데이터들에 대해 얼마만큼의 비중을 둘 것인가에 대한 수치로 이해하면되며, 편향은 하나의 뉴런을 통해 나오는 결과를 조절해주는 역할이라고 보면 된다.
하나의 뉴런에 들어오는 입력값을 x, 해당 입력에 대한 가중치를 w, 결과를 조정하기 위한 편향을 b 라고 할 때, 뉴런에서 출력되는 값인 y 는 아래와 같이 표현할 수 있다.
$ y = wx + b $
계산된 y 값들은 활성화 함수(Activation Function) 에 의해 합으로 처리되어 최종적인 출력값이 나오게 되고, 이렇게 계산된 출력값은 다시 다음 은닉층의 입력으로 사용되게 된다. 이를 입력 값이 n개인 상황이라면 아래 그림과 같이 나타낼 수 있다.

위의 그림에서처럼 입력층으로부터 입력을 받아 은닉층을 통해 출력층으로 전달되어 최종 예측값을 출력해준다. 위의 과정을 수식으로 표현하면 아래와 같이 표현할 수 있다.
$ \hat{y} = w_0x_0 + w_0x_1 + … + w_{n-2}x_{n-2} + w_{n-1}x_{n-1} $
2) 역방향 전파(Back Propagation)
역전파는 앞서 언급한 데로 실제 결과 값과 예측 결과 값의 오차를 계산해서 가중치를 업데이트 하는 과정이다. 이 때, 오차부터 역방향으로 1단계씩 미분 값을 계산하고, 계산된 미분 값을 체인 룰에 의해 곱해가면서 가중치에 대한 그레디언트를 계산한다.
연산과 관련된 부분은 뒤에 나올 경사하강법 부분에서 좀 더 살펴보기로 하자.
2. 최적화 (Optimization)
다음으로 알아볼 내용은 최적화(Optimization) 이다. 본래 최적화란, 특정 제약조건이 있을 수 있는 상황속에서, 여러 가지 입력값을 넣어가며, 정해진 기준에 최대한 부합하는 값을 선택하는 방법론을 의미한다. 최적화 기법에는 여러 종류가 있는데, 이번 장에서 알아볼 경사하강법 역시 최적화 알고리즘에 대표적인 예시라고 할 수 있다.
최적화 알고리즘에 대해서는 이 후에 좀 더 다룰 예정이므로 이번 장에서는 정의와 경사하강법이 최적화 알고리즘이구나 정도만 알고 넘어가면 될 것이다.
3. 미분
이번 장의 제목은 Gradient Descent 인데 갑자기 왠 미분이냐고 의문이 들 수 있다. 하지만, 미분과 Gradient Descent 와의 연관성은 매우 중요하고, 이후에 살펴볼 신경망의 동작원리에서도 사용될 만큼 중요하기에 시작에 앞서 먼저 살펴보자.
미분이란, 임의의 그래프에서 특정 시점에 대한 순간 변화율 혹은 기울기라고 배웠을 것이다. 수식으로 표현하자면 아래와 같다.
$ \frac {f(x+t) - f(x)} {t} $
위의 수식에서 t 는 시간을 의미하며 매우 작은 값으로 가정하며, x 값이 t 만큼의 시간이 흐르기 전 후의 비교량은 결국 순간의 변화율을 의미하는 것과 같다.
4. 손실함수 (Loss Function)
앞서 경사하강법은 함수의 최소값을 찾는 과정이라고 했다. 이 때 적용 대상인 함수가 바로 손실함수인데, 손실함수란, 우리가 만든 혹은 사용하는 알고리즘이 얼마나 잘못하고 있는지를 표현하는 지표이며, 다른말로 비용함수(Cost Function) 이라고도 부른다.
만약 학습이 잘됬다면, 손실함수의 값은 작게 표현될 것이며, 이는 정답과 알고리즘 출력인 예측결과를 비교하는 데 사용된다. 앞선 장에서 학습 과정에서 출력되는 loss 와 val_loss 가 이에 해당한다.
손실함수에는 여러 종류가 있지만, 가장 많이 만나볼 손실함수는 MSE(평균제곱오차, Mean Squared Error) 와 CEE(교차 엔트로피 오차, Cross Entropy Error) 가 있다.
1) MSE (평균 제곱오차, Mean Squared Error)
단어 뜻 그대로, 실제 결과와 예측 결과 간의 오차에 제곱을 하고 평균을 낸 결과에 대한 함수이다. 수식으로는 아래와 같이 표현된다.
$ Error = \frac {1} {2} \sum _i^n {(y_i - {\hat{y}}_i)}^2 $
위의 수식에서 $ y_i $ 는 실제 결과 값을, $ y^i $ 는 예측 결과 값을 의미한다. 위의 수식은 앞서 회귀 부분에서 다룬 적이 있기에 예제는 생략하도록 하겠다.
2) CEE (교차 엔트로피 오차, Cross Entropy Error)
설명에 앞서 먼저 엔트로피의 정의부터 살펴보자. 엔트로피라는 단어는 무질서도를 의미하는 단어인데, 물리를 배웠던 사람이라면 익숙한 단어일 것이다. 열역학에서는 유용하지 않은 에너지의 흐름을 의미하는 용어이고, 지금부터 설명하려는 엔트로피는 이러한 특징을 정보공학으로 가져온 개념이다.
정보공학에서의 엔트로피란 정보량의 기댓값(평균)을 의미한다. 만약 어떤 사건이 항상 발생하는 사건이라면 발생할 확률은 1이 되기 때문에, 이것이 갖고 있는 정보량은 0이 된다. 즉, 일어나는 확률이 적을 수록 많은 정보를 담고 있으며, 엔트로피의 값은 커지게 된다는 의미이다.
이를 수식으로 표현하게되면 아래와 같다.
$ Error = \sum _{i=1}^n P(x_i)I(x_i) = - \sum _{i=1}^n P(x_i) \log _b P(x_i) $
예를 들어 동전 던지기를 한다고 가정해보자. 이 때 동전에 대한 엔트로피는 다음과 같다.
$ H(X) = - (0.5 \log _2{0.5} + 0.5 \log _2{0.5}) = 0.5 + 0.5 = 1 $
위의 결과와 같이 앞면이 나올지, 뒷면이 나올지 확률은 0.5 이기 때문에 엔트로피의 값은 1이 되고, 이는 정보량이 최대인 상태라고도 표현할 수 있다.
위의 내용을 모델이 학습하는 과정에 대입해보면 아래와 같이 표현할 수 있을 것이다. 설명하기에 앞서 이해를 돕기위해 아래 설명에서 등장하는 “확률분포” 이라는 표현은 “이산확률분포”가 정확한 표현이라는 점을 감안해주기 바란다.
먼저, 실제 결과에 대한 확률분포를 p라고 표현하고, 예측 결과에 대한 확률분포를 q라고 표현할 때, 엔트로피 식을 아래와 같이 바꿀 수 있다.
$ H(p, q) = - \sum _i p_i \log {q_i} $
또한, 2개의 확률 분포가 존재할 때, 두 확률 분포의 거리(오차) 계산은 쿨백-라이블러 발산(Kullback-Leibler Divergence, KL-Divergence) 으로 나타내며, 확률분포 p 를 기준으로 확률분포 q 가 얼마나 다른지를 나타낸다. 수식으로는 아래와 같이 나타낸다.
$ D_{KL}(p \parallel q) = \sum _i p_i \log { \frac {p_i} {q_i} } $
위의 2가지를 이용해서 정리하면, 아래와 같이 표현할 수 있다.
$ H(p, q) = - \sum i p_i \log {q_i} $
$ = - \sum _i p_i \log q_i - \sum _i p_i \log {p_i} + \sum _i p_i \log {p_i} $
$ = H(p) + \sum _i p_i \log {p_i} - \sum _i p_i \log q_i $
$ = H(p) + \sum _i p_i \log \frac {p_i} {q_i} $
$ = H(p) + D{KL}(p \parallel q) $
위의 수식을 통해서 알 수 있듯이, 실제 결과 값(확률 분포 p)을 기준으로 봤을 때, 교차 엔트로피 오차는 실제 결과 값에 대한 엔트로피에 두 결과의 엔트로피에 대한 오차를 더해줌으로써 계산이 가능하다. 이 때, 실제 결과값에 대한 엔트로피는 자체가 불변의 값이기 때문에, 만약 손실함수를 교차 엔트로피 오차함수를 사용한다면, 오차를 최소화 하기 위해서는 두 결과 간의 차이에 대한 엔트로피 값을 조절해줘야 한다. 위의 수식에서 사용된 쿨백-라이블러 발산에 대해 궁금한 사람은 아래의 참고 자료에 링크를 참조하기 바란다.
5. 경사하강법
자, 그렇다면 앞서서 배운 여러 지식들이 어떻게 경사하강법이라는 것과 연관이 있는지 알아보자. 경사하강법이라는 것을 위키백과에서 검색하게되면 아래와 같이 정의되어있다.
경사하강법
1차 근삿값 발견용 최적화 알고리즘이다. 기본 개념은 함수의 기울기(경사)를 구하고 경사의 절댓값이 낮은 쪽으로 계속 이동시켜 극값에 이를 때까지 반복시키는 것이다.
출처: 위키백과
즉, 해당함수의 최소값이 되는 입력값을 찾기 위해, 초기 입력값부터 함수의 순간기울기를 계산하고, 기울기가 낮은 방향으로 입력값을 바꿔가며, 함수의 최소값을 찾는 방법이라고 할 수 있다. 정확히는 특정변수에 대해 편미분을 하는 것이며, 편미분이라함은 특정 함수를 구성하는 여러 변수들 중 1개를 제외한 나머지는 상수로 취급하고 미분을 하는 방법을 의미한다.<ㅠㄱ>
1) 역방향 전파(Back Propagation)
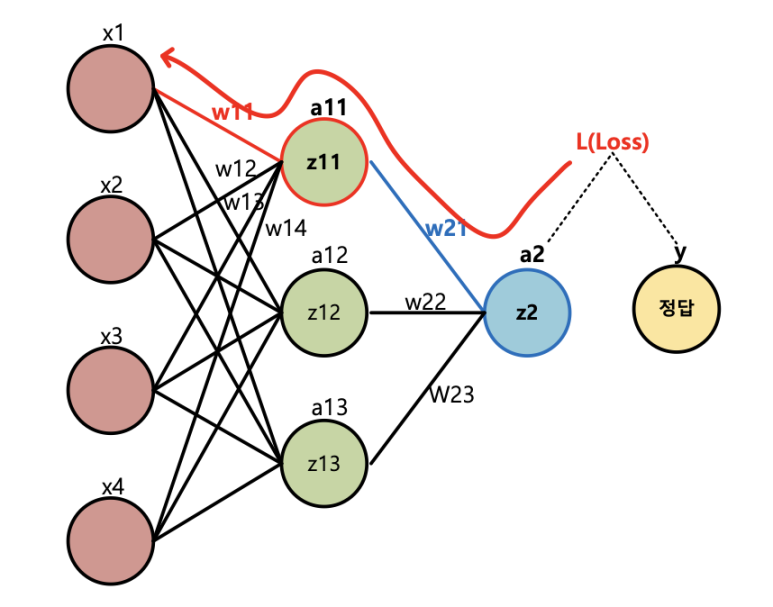
이 장의 맨처음에 언급했던 데로, 경사하강법이 적용되는 부분은 역전파를 통해 가중치가 업데이트되는 과정에서 등장하게 된다. 이해를 돕기위해 예시로 아래의 그림처럼 각 노드에 대한 값과 해당 노드의 값에 대한 함수식이 아래의 내용과 같다고 가정해보자.
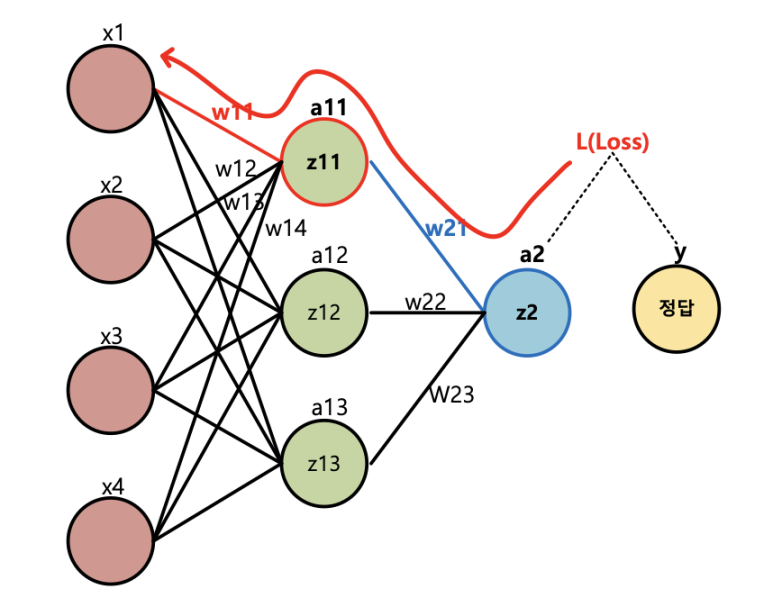
앞서 역전파 과정은 손실에서부터 학습방향의 역방향으로 한 단계씩 미분한 결과를 계산하고 가중치를 업데이트 한다고 말했다. 위의 예시에서처럼 최종적으로 W11 에 대해 업데이트 한다고 가정하면, 각 단계별 미분의 결과는 아래와 같이 계산될 것이다.
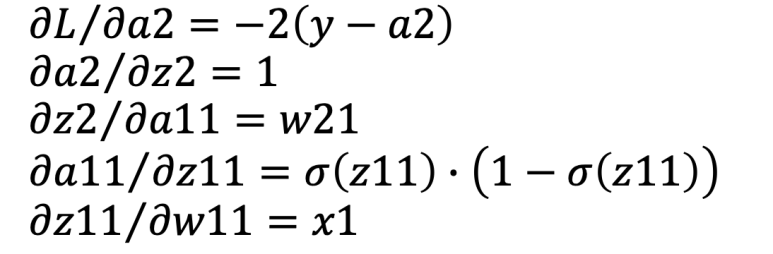
최종적으로 계산하려는 결과는 가중치 W11 에 대한 그레디언트는 다음과 같이 체인 룰로 연산이 가능하다.

2) 그레디언트(Gradient)의 의미
자, 그러면 이제 경사하강법에 대해서 좀 더 정확하게 정의를 내려보자. 경사하강법이란, 손실함수의 미분인 그레디언트(Gradient) 를 이용해서 가중치를 업데이트 하는 방법 이라고 현 단계까지의 내용으로 정의할 수 있다. 수식으로 표현하면 다음과 같다.
$ W_{new} = W_{old} + \alpha $
위의 수식에서 $ \alpha $에 대한 값은 미분값이며, 이는 다음과 같이 정의할 수 있다.
$ W_{new} = W_{old} - \eta {\nabla }_wL $
$ \alpha $에 해당하는 부분을 좀 더 살펴보면 아래 그림과 같이 나타낼 수 있다.
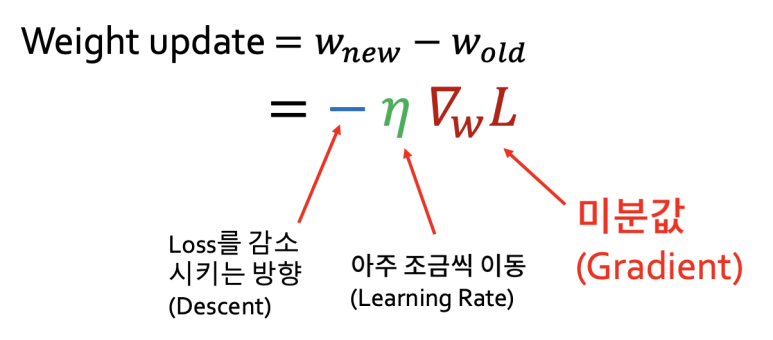
해석을 하면, 미분값인 그레디언트를 손실(Loss)이 감소하는 방향으로 학습률(Learning Rate) 만큼 이동하겠다는 의미이다. 이를 그래프로 표현하면 아래와 같이 나타낼 수 있다.
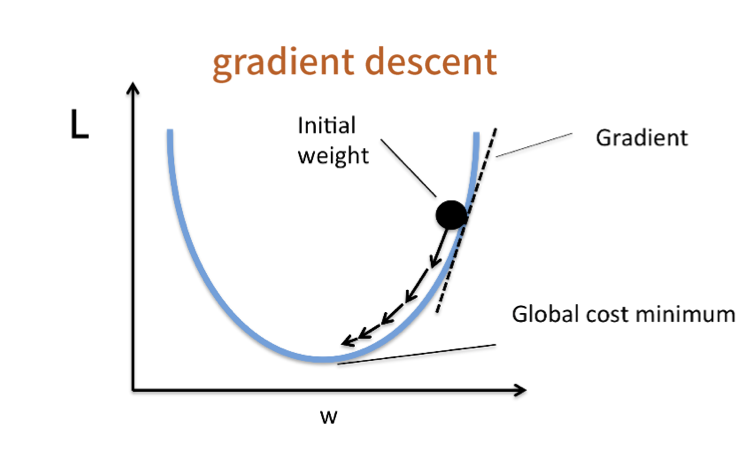
위의 과정처럼 계산되는 그레디언트 값은 양수가 될 것이다. 하지만 앞서 언급한 것처럼 손실이 작아지는 방향은 음의 방향으로 이동해야 되기 때문에, 수식에서 음의 기호가 붙은 것이다. 이렇게 초기 가중치부터 손실이 감소하는 방향으로 가중치의 값을 조금씩 조정하게되며, 최종적으로 기울기가 0이 되는 지점에서 학습이 종료하게 된다.
자, 그렇다면 최종적으로 결론을 내려보자. 결과적으로 경사하강법이라 함은, 손실이 감소하는 방향으로 학습률 만큼 값을 조금씩 이동시킴으로써 신경망의 손실함수에 대한 오차를 줄이는 방법이라고 정의할 수 있다.
6. 학습률 (Learning Rate)
학습률은 그레디언트가 이동하는 크기(보폭)이라고 표현할 수 있다. 학습률은 앞선 예제에서처럼 모델을 컴파일하는 과정에서 설정할 수 있는데, 최종적으로 계산해야되는 기울기의 크기는 학습률과 비례하는 관계에 있기 때문에 적절한 값으로 설정해주는 것이 중요하다. 어떤 의미인지 좀 더 알아보기 위해 예시로 아래와 같은 함수가 있다고 가정해보자.
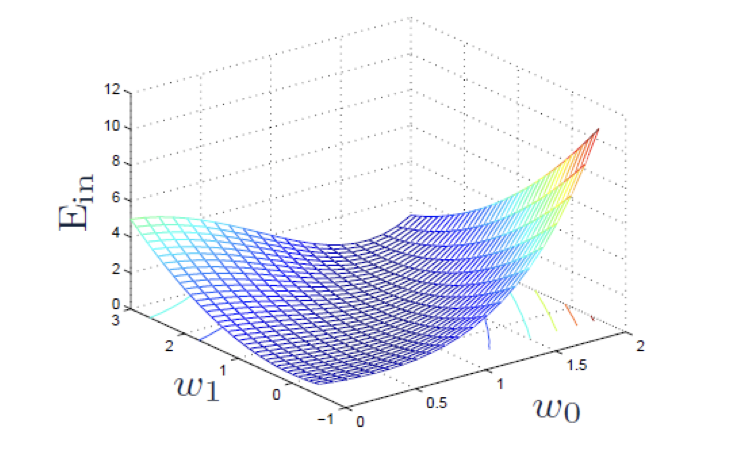
해당 함수에 대해 경사하강법을 적용할 것이며, 변하는 값은 학습률에 대해서만 변경해줬을 때, 다음과 같이 경사하강법이 진행되었다.
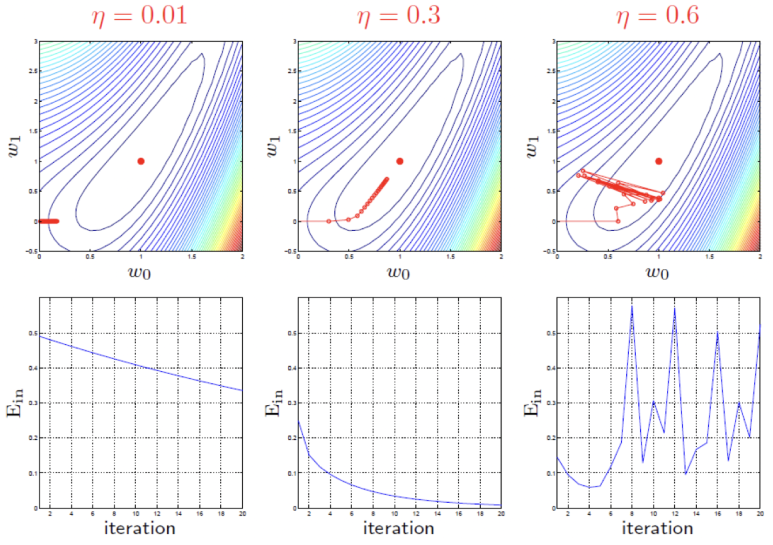
위의 결과에서 중앙의 빨간 점이 최적점이며, 화살표는 실제 해당 학습률로 경사하강법을 진행했을 때의 진행 방향 및 이동 크기를 나타낸 것이다. 3개의 사진을 비교하면 알 수 있듯이, 학습률을 너무 작게 설정하면, 같은 시간동안 그레디언트가 이동한 크기가 너무 작으며, 반대로 너무 클 경우, 맨 오른쪽 결과처럼 최적점에 도달하지 못하거나, 최적점을 지나치고 발산을 하는 경우를 볼 수 있다. 위의 3가지 중에서는 학습률을 0.3 으로 설정한 결과가 학습률을 잘 설정했다고 할 수 있다.
7. 경사하강법의 종류
경사하강법의 종류라고 표현했지만, 정확히는 입력 데이터의 양을 어떻게 설정할 것인가에 따른 분류라고 할 수 있다. 크게 3가지 방법이 있는데 내용은 다음과 같다.
1) 배치 경사하강법(Batch Gradient Descent)
일반적으로 컴퓨터와 관련해서 Batch 라고 하면, 일괄적으로 처리되는 작업을 의미하는 경우가 많다. 비슷한 맥락으로 배치 경사하강법은 입력데이터를 한번에 넣어서 최적의 1개 스텝으로 학습을 진행하는 방식이다. 물론 학습되는 양이 많기 때문에 결과는 좋게 나올 수 있지만, 학습에 소요되는 시간이 오래걸리고, 데이터의 용량이 크면, 메모리도 부족할 수 있다는 단점이 있다.
2) 확률적 경사하강법(Stocastic Gradient Descent)
앞서 배치 경사하강법의 경우, 한 번 학습할 때 사용되는 데이터의 양이 많아, 소요되는 시간이 너무 많다는 단점이 있다. 이를 해결하기 위해 입력 데이터를 최대한 작은 단위로 나눠서 일부의 데이터만 학습을 시키는 방법이다.
이럴 경우, 앞서본 배치 경사하강법보다는 학습시간이 적게 소요될 수 있지만, 학습 정확도의 측면에서는 같은 데이터를 다시 사용할 수 있다는 점이 있어 원할하게 진행되지 않는다.
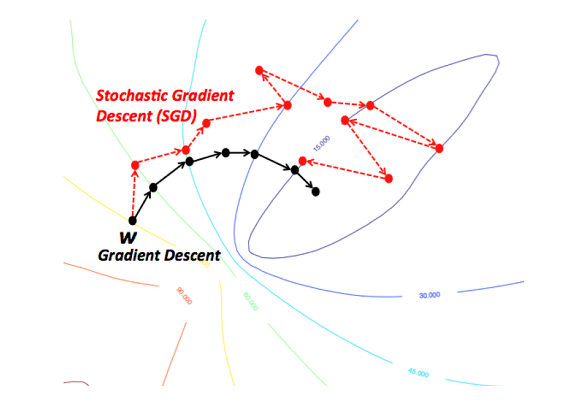
3) 미니배치 경사하강법(Mini batch Gradient Descent)
앞서 본 배치 경사하강법과 확률적 경사하강법에 존재하는 장점만을 가져온 경사하강법으로, 학습속도와 정확도 모두 배치 경사하강법과 확률적 경사하강법의 중간쯤에 위치한다고 할 수 있다.
만약, GPU를 사용한다면, 미니배치 방법을 적용했을 때, 가중치 업데이트 속도는 상승할 것이며, 이는 GPU의 특성상 병렬처리 및 계산에 특화되어 있기 때문이다. 뿐만 아니라 학습률과 배치 사이즈 서로 상관관계가 있어, 만약 학습률을 기존의 2배로 증가시켰다면, 배치 크기 역시 2배로 증가시켜주는 것이 학습에 있어 효율적일 것이다.
8. 실습: 얕은 신경망과 경사하강법
이번 실습에서는 각 10개의 무작위점을 기준으로 주변에 10개 점씩 추가하며, 예측 대상은 무작위 점 10개를 통해 기준점 10개의 라벨로 분류하는 것이다.
우선 데이터를 생성하기 앞서, 먼저 모델부터 생성하도록 하자. 이번에는 1장에서 나온 내용 중 모델 서브클래싱 방식을 이용해서 구현할 것이다.
[Python Code]
import numpy as np
import tensorflow as tf
# 하이퍼파라미터 설정
EPOCHS = 200
# 네트워크 정의
class MyModel(tf.keras.Model):
def __init__(self):
super(MyModel, self).__init__()
self.d1 = tf.keras.layers.Dense(128, input_dim=2, activation='sigmoid')
self.d2 = tf.keras.layers.Dense(10, activation='softmax')
def call(self, x, training=None, mask=None):
x = self.d1(x)
return self.d2(x)
앞서 1장에서 나온대로 서브클래싱 방법을 사용할 때는 반드시 __init() 메소드와 call() 메소드를 오버라이딩 해줘야한다. 또한 모델 초기화와 동시에 신경망의 구조를 같이 설정해줬다. 입력값은 x, y 좌표로 2개이고, 은닉층은 128개의 노드로, 출력은 10개 노드로 구성했다.
다음으로 학습 방법을 정의해주자. 이번 예제에서는 경사하강법을 이용해서 가중치 업데이트 하는 과정을 저수준 API 방식으로 구현할 것이다. 이를 위해선 먼저 그레디언트를 계산하기 위해 tensorflow 2.x 에서 제공하는 기능인 Auto Gradient(자동미분) 기능을 사용할 것이다. 우선 아래와 같이 코드를 작성해보자.
[Python Code]
# 학습 루프 정의
@tf.function
def train_step(model, inputs, labels, loss_object, optimizer, train_loss, train_metric):
# 그레디언트 계산
with tf.GradientTape() as tape:
predictions = model(inputs)
loss = loss_object(labels, predictions)
gradients = tape.gradient(loss, model.trainable_variables) # df(x) / dx
optimizer.apply_gradients(zip(gradients, model.trainable_variables))
train_loss(loss)
train_metric(labels, predictions)
위의 코드를 보면 GradientTape() 이라는 함수가 사용됬는데, 이 부분은 해당 객체가 생성된 이후로 수행되는 모든 연산의 결과를 마치 카세트 테이프처럼 기록한다. 그 다음 .gradient() 메소드를 통해 해당 메소드가 등장하기 전까지의 모든 연산 결과에 대해 미분을 하여 그래디언트를 계산한다.
그 다음으로 눈에 들어오는 것은 @tf.function 이다. 해당 어노테이션 역시 1장에서 언급한 것처럼, train_step() 을 사용하는 모든 함수에서 적용가능하도록 설정해주는 부분이다.
이렇게 모델과 학습 방법을 설정했다면, 다음으로 데이터를 생성해주자. 임의의 점을 생성하기 위해서 넘파이의 random 함수를 사용한다.
[Python Code]
# 데이터 셋 생성 & 전처리
np.random.seed(0)
## 각 10개의 무작위 점들에 대해서 구분하는 모델 생성 예정
pts = list()
labels = list()
center_pts = np.random.uniform(-8.0, 8.0, (10, 2))
for label, center_pt in enumerate(center_pts):
for _ in range(100):
pts.append(center_pt + np.random.rand(*center_pt.shape))
labels.append(label)
pts = np.stack(pts, axis=0).astype(np.float32) # GPU를 사용할 경우 float32 형으로 변환해서 넣어줘야함
labels = np.stack(labels, axis=0)
시작할 때 말했던 것처럼 무작위로 10개의 중심점을 찍고, 그 점을 기준으로 10개씩 랜덤한 위치에 점을 찍는다. 물론 랜덤 값을 다시 넣어도 동일한 결과가 나오도록 seed() 값을 설정한 후에 사용했다.
총 100개의 점이 결정됬다면, 해당 값을 넘파이의 stack 함수를 사용해서 정리해준다. 이 때, 학습에 사용되는 장치에 따라 추가적인 형 변환이 들어가는데, GPU를 사용해서 학습하는 경우에는 입력 데이터를 float32 형으로 변환을 해줘야하며, 그 외에는 형 변환을 할 필요는 없다.
위의 과정까지 완료됬다면, 텐서플로를 사용하기에 알맞은 형태로 학습 데이터를 만들어주자.
[Python Code]
train_ds = tf.data.Dataset.from_tensor_slices((pts, labels)).shuffle(1000).batch(32)
위의 코드에서처럼 Dataset 의 from_tensor_slices() 함수를 사용해 데이터셋 형태로 바꿔주며, 각 포인트들과 라벨을 포함시켜서 짝을 맞춰준다. 그리고 랜덤하게 셔플링을 한 후, 1개 배치마다 32개씩 사용하도록 설정해준다.
데이터까지 생성 완료했기 때문에 모델 객체를 생성하고, 학습을 진행하도록 하자.
[Python Code]
model = MyModel()
loss_object = tf.keras.losses.SparseCategoricalCrossentropy()
optimizer = tf.keras.optimizers.Adam()
train_loss = tf.keras.metrics.Mean(name='train_loss')
train_accuracy = tf.keras.metrics.SparseCategoricalAccuracy(name='train_accuracy')
# 학습 루프
for epoch in range(EPOCHS):
for x, y in train_ds:
train_step(model, x, y, loss_object, optimizer, train_loss, train_accuracy)
template = 'Epoch {}, Loss: {}, Accuracy: {}'
print(template.format(epoch+1, train_loss.result(), train_accuracy.result() * 100))
[실행 결과]
Epoch 1, Loss: 0.1438901275396347, Accuracy: 98.69353485107422
Epoch 2, Loss: 0.14318959414958954, Accuracy: 98.69999694824219
Epoch 3, Loss: 0.14249573647975922, Accuracy: 98.70640563964844
Epoch 4, Loss: 0.14180870354175568, Accuracy: 98.7127456665039
Epoch 5, Loss: 0.1411280483007431, Accuracy: 98.71902465820312
...
Epoch 196, Loss: 0.07336199283599854, Accuracy: 99.33686828613281
Epoch 197, Loss: 0.07317738234996796, Accuracy: 99.33853912353516
Epoch 198, Loss: 0.07299371063709259, Accuracy: 99.34020233154297
Epoch 199, Loss: 0.07281097769737244, Accuracy: 99.34185791015625
Epoch 200, Loss: 0.07262912392616272, Accuracy: 99.343505859375
학습에 사용할 손실함수는 SparseCategoricalCrossEntropy 를 사용하고, 최적화 함수는 Adam을 사용한다.
그 외에 손실에 대한 함수와 정확도 지표까지 설정해준다.
이 후 앞서 정의한 학습 방식 함수인 train_step() 함수를 사용해서 학습을 진행한다. 학습 초기에는 정확도가 98.69였지만, 최종적으로는 99.34까지 상승한 것을 확인할 수 있다.
[참고자료]
쿨백-라이블러 발산 참고자료
https://datascienceschool.net/02%20mathematics/10.03%20%EA%B5%90%EC%B0%A8%EC%97%94%ED%8A%B8%EB%A1%9C%ED%94%BC%EC%99%80%20%EC%BF%A8%EB%B0%B1-%EB%9D%BC%EC%9D%B4%EB%B8%94%EB%9F%AC%20%EB%B0%9C%EC%82%B0.html

댓글남기기