[Python Deep Learning] 2. 회귀 (Regression)

2020-11-08 9 분 소요

python_deep_learning

1. 회귀

영국의 유전학자 갈튼이 생각한 문제로, 출력 변수와 입력변수가 선형관계를 가정하는 단순한 통계 분석 기법으로 하나 이상의 특성과 연속적인 타깃 변수 사이의 관계를 모델링 하는 것이다. 갈튼은 부모의 키 평균과 자녀의 키 평균을 비교하면, 자녀의 키가 부모의 키보다는 평균에 가까워진다는, 평균으로 되돌아온다는 경향을 보인다고 지적했다. 즉, 회귀란 데이터에 대한 평균값들의 연속적인 집합이라고 볼 수 있다. 그리고 회귀에서 입력으로 사용되는 변수를 독립변수, 출력으로 사용되는 변수는 종속변수라고 부른다. 그리고 독립변수와 종속변수의 관계에 따라 단순 선형 회귀와 다중 선형 회귀로 크게 나눠볼 수 있다.

1) 단순 선형 회귀

학습 데이터의 경향성을 가장 잘 설명하는 하나의 직선을 예측하는 모형이라고 할 수 있으며, 주어진 데이터로 근사하는 선형 함수로 표현한다. 수식으로 표현하면 아래와 같다.

$ y = wx + b $

위의 내용을 1장에서 살펴본 신경망인 퍼셉트론으로 표현하면, 아래 그림처럼 표현할 수 있다.

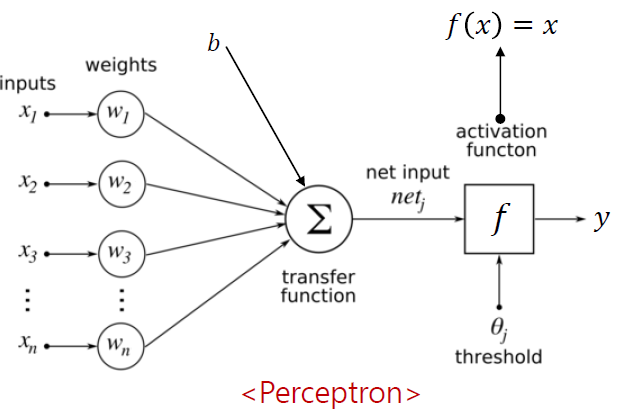
퍼셉트론 개념도

갑자기 선형회귀에서 왠 신경망이 나오냐에 의아할 수 있다. 간단하게 설명하자면, 선형회귀로 데이터를 분류하던 와중에 데이터가 선형의 관계가 아닌 경우에는 선형회귀 모델을 구현하여 분류할 수 없다. 대표적인 예시가 XOR 문제이다. 자세한 내용은 딥러닝개론에서 설명했으며, 궁금한 사람은 아래 링크에서 확인할 수 있다.

[DeepLearning 101] 1. 딥러닝의 역사

XOR 와 같이 선형관계가 없는 데이터를 분류하기 위해 등장한 것이 퍼셉트론이며, 사실 신경망의 본질이 선형모델이기 때문이다. 이러한 이유로 회귀라는 주제에서 신경망을 언급한 것이다.
위의 내용을 응용해서 아래 실습 예제를 수행해보자. 예제는 통계청에서 조사한 2018년 한국의 지역별 인구증가율과 고령인구비율에 대한 데이터이다.

지역	인구증가율	고령인구비율
인천	0.3	12.27
서울	-0.78	14.44
경기	1.26	11.87
강원	0.03	18.75
충남	1.11	17.52
세종	15.17	9.29
충북	0.24	16.37
경북	-0.24	19.78
전북	-0.47	19.51
대전	-0.77	12.65
대구	-0.37	14.74
울산	-0.85	10.72
전남	-0.41	21.94
광주	-0.27	12.83
경남	0.02	15.51
부산	-0.76	17.14
제주	2.66	14.42

위의 데이터를 한 눈에 보기 편하게 시각화를 하면 아래의 그림과 같다.

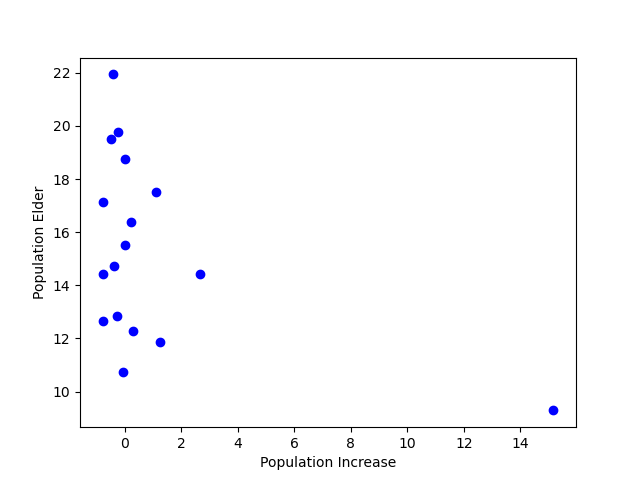
샘플 데이터

위의 그래프에서 오른쪽 하단에 치우친 점이 하나 있는데 이를 이상치(Outlier) 라고 한다. 회귀모델의 경우 이상치에 영향을 많이 받으며, 이상치를 처리할 때는 반드시 필요유무 및 원인 분석을 한 후에 처리를 판단하는 것이 좋다. 위의 예시에서는 제거해도 무방하다고 보기 때문에 제외하도록 한다. 이상치를 뺀 나머지 데이터에 대한 분포는 아래 그림과 같다.

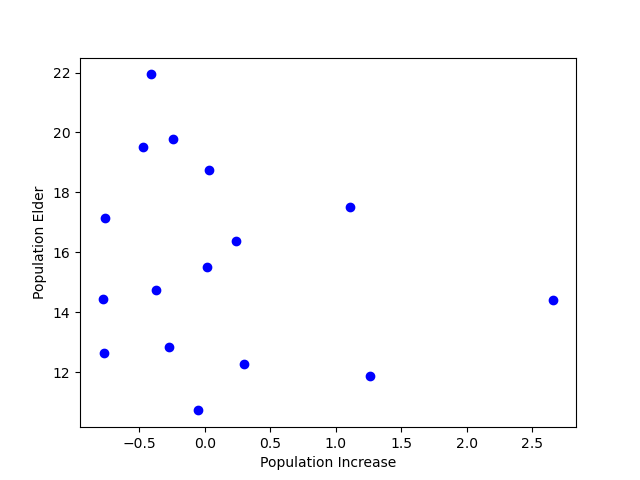
샘플 데이터 이상치 제거 결과

위의 데이터를 사용해서 선형 회귀 모델을 만들어보자. 데이터의 경샹성을 가장 잘 설명하는 직선과 각 데이터 간의 거리(차이) 를 잔차라고 하는데, 잔차의 제곱을 최소화 하는 알고리즘을 최소 제곱법이라고 한다. 이번예제에서는 최소제곱법으로 선형회귀선인 y=ax+b 의 기울기 a 와 y 절편인 b 를 구할 수 있다. 이에 대한 수식은 다음과 같다.

$ a = \frac {\sum _{i=1}^n(y_i - \hat{y}) (x_i - \hat{x})} {\sum _{i=1}^n{(x_i - \hat{x})}^2} , b = \hat{y} - a \hat{x} $

위의 수식에서 xi , yi 는 각 입력 데이터 이고, x_hat 과 y_hat 은 각각 평균을 의미한다. 위의 내용을 코드로 구현한 것이 아래의 내용이다.

[Python Code]

x = population_inc[:5] + population_inc[6:]
y = population_old[:5] + population_old[6:]

x_bar = sum(x) / len(x)
y_bar = sum(y) / len(y)

a = sum([(y - y_bar) * (x - x_bar) for y, x in list(zip(y, x))])
a /= sum([(x - x_bar) ** 2 for x in x])
b = y_bar - a * x_bar

print('a: ', a, ', b: ', b)

[실행 결과]

a:  -0.6995837173734697 , b:  15.719335973503764

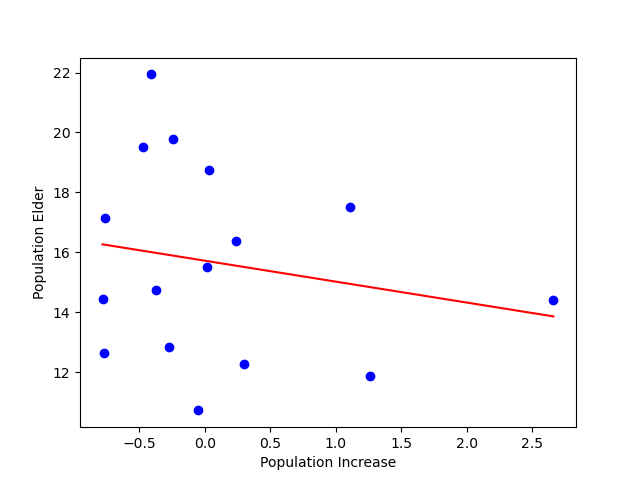
회귀모형 수식구현

이번에는 앞선 코드와 같이 복잡한 수식으로 구현하는 것이 아니라, 텐서플로를 이용해서 회귀선을 계산하는 코드를 구현해보자.

[Python Code]

import numpy as np
import pandas as pd
import random
import tensorflow as tf

x = population_inc
y = population_old

a = tf.Variable(random.random())
b = tf.Variable(random.random())

def compute_loss():
    y_pred = a * x + b
    loss = tf.reduce_mean((y- y_pred) ** 2)

    return loss

optimizer = tf.optimizers.Adam(lr = 0.07)
for i in range(1000):
    optimizer.minimize(compute_loss, var_list=[a, b])

    if (i + 1) % 100 == 0:
        print(i+1, 'a: ', a.numpy(), ', b: ', b.numpy(), ', loss: ', compute_loss().numpy())

[실행 결과]

a:  0.38390833 , b:  6.8514504 , loss:  87.261215
a:  -0.16095385 , b:  11.3204565 , loss:  28.639748
a:  -0.47758487 , b:  13.905612 , loss:  12.760078
a:  -0.6245779 , b:  15.1065 , loss:  9.878871
a:  -0.6789176 , b:  15.550483 , loss:  9.535722
a:  -0.6949609 , b:  15.681566 , loss:  9.508943
a:  -0.69875115 , b:  15.712533 , loss:  9.507578
a:  -0.69946456 , b:  15.718363 , loss:  9.50753
a:  -0.69957006 , b:  15.719227 , loss:  9.507532
a:  -0.69958156 , b:  15.71932 , loss:  9.507531

회귀모형 텐서플로

결과는 수식을 코드화 한 결과와 유사하다. 다만, 신경망의 초기 값을 random() 으로 구현하였기 때문에, 시도할 때마다 결과가 달라질 수 있다. 이번에는 코드를 좀 더 살펴보도록 하자. 가장 먼저 기울기인 a 와 y 절편인 b 를 랜덤 값으로 초기화한 다음, 잔체의 제곱의 평균을 구하는 함수를 정의한다. 기대출력인 Y에서 모델의 예측 결과인 y_pred를 빼는 과정이 있는데, 차이를 잔차라고 앞서 언급했다. 계산된 잔차의 제곱을 모두 더해서 평균 낸 값으로 손실을 계산한다. 딥러닝을 포함한 머신러닝의 주요 알고리즘은 학습에 대한 손실을 최소화하는 것이 주요 목적 중 하나이다.
끝으로 최적화 함수는 복잡한 미분 계산 및 가중치 업데이트를 자동으로 진행해주는 도구이다. 최적화 함수는 적당한 학습률을 넣어주면 안정적이고 효율적으로 학습한다. 일반적으로 학습율은 0.1 ~ 0.0001 사이의 값을 사용한다. 이를 바로 다음줄부터 등장하는 반복문안에서 수행을 하게 되는데, minimize() 메소드를 사용해 최소화할 손실을 메소드의 첫 번째 파라미터에 전달하고, 두 번째 파라미터는 학습 변수들을 리스트 형식으로 전달한다.

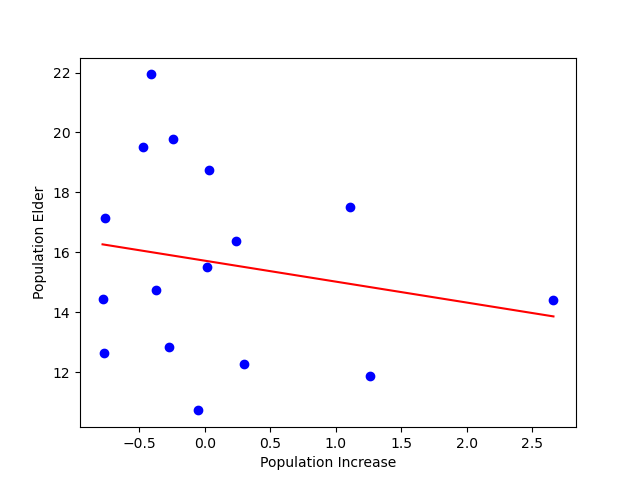
위의 내용을 1000번 반복하면, 실행 결과와 같이 a 와 b 가 잔차 제곱의 평균을 최소화하는 적절한 값에 도달하고 이를 연속적인 직선으로 표현한 것이 시각화 부분의 붉은 직선이다.
시각화의 결과는 수식으로 표현한 것과 퍼셉트론으로 학습했을 때의 결과 모두 동일하게 나오며, 이를 통해 텐서플로를 활용해 신경망으로 학습하는 것이 얼마나 쉬운지까지 확인했다.

2) 다중 선형 회귀

앞서 살펴본 것은 선형회귀, 그 중에서도 변수가 1개인 단순선형회귀에 대해서 살펴봤다. 하지만 현실의 문제에서는 여러 가지의 변수들이 존재하기 때문에 이를 회귀 식으로 표현하기 위해서는 다항 회귀를 사용하는 것이 적절하다. 뿐만 아니라 단일입력이 아닌 다중입력을 받기 때문에 변수가 확장되어 벡터의 내적 형태로 수식을 작성할 수 있다.
이번 절에서는 다항회귀, 그 중에서 비선형 회귀를 신경망으로 어떻게 학습하는 지를 살펴보기로 하자. 우선 다항회귀는 직선이 아닌 2차, 3차 함수와 같은 곡선형이다. 예시를 위해 아래에 나온 2차함수 코드를 실행해보자.

[Python Code]

import numpy as np
import random
from matplotlib import pyplot as plt

import tensorflow as tf

x = [0.3, -0.78, 1.26, 0.03, 1.11, 0.24, -0.24, -0.47, -0.77, -0.37, -0.85, -0.41, -0.27, 0.02, -0.76, 2.66]
y = [12.27, 14.44, 11.87, 18.75, 17.52, 16.37, 19.78, 19.51, 12.65, 14.74, 10.72, 21.94, 12.83, 15.51, 17.14, 14.42]

a = tf.Variable(random.random())
b = tf.Variable(random.random())
c = tf.Variable(random.random())

def compute_loss():
y_pred = a * x * x + b * x + c
loss = tf.reduce_mean((y - y_pred)**2)

    return loss

optimizer = tf.keras.optimizers.Adam(lr=0.07)
for i in range(1000):
# 잔차제곱의 평균을 최소화시킴
optimizer.minimize(compute_loss, var_list=[a,b,c])

    if i % 100 == 99:
        print(i, 'a : ', a.numpy(), ' ,b: ', b.numpy(), ' ,c: ', c.numpy(), ' ,loss: ', compute_loss().numpy())

line_x = np.arange(min(x), max(x), 0.01)
line_y = a * line_x * line_x + b * line_x + c

plt.plot(line_x, line_y, 'r--')
plt.plot(x, y, 'bo')
plt.xlabel('Population Growth Rate (%)')
plt.ylabel('Eldery Population Rate (%)')

[실행결과]

a :  3.8019838  ,b:  -5.1587806  ,c:  6.2514377  ,loss:  71.53412
a :  2.822443  ,b:  -4.7601194  ,c:  10.201875  ,loss:  32.286655
a :  1.3649138  ,b:  -2.5580266  ,c:  12.838653  ,loss:  16.520706
a :  0.38468897  ,b:  -1.0172037  ,c:  14.495486  ,loss:  11.165136
a :  -0.15211624  ,b:  -0.17264327  ,c:  15.401946  ,loss:  9.77893
a :  -0.40635747  ,b:  0.22731057  ,c:  15.831422  ,loss:  9.503637
a :  -0.5111243  ,b:  0.39211902  ,c:  16.008408  ,loss:  9.461542
a :  -0.54874855  ,b:  0.45130548  ,c:  16.071968  ,loss:  9.45659
a :  -0.56051296  ,b:  0.46981156  ,c:  16.091845  ,loss:  9.456142
a :  -0.56370384  ,b:  0.474831  ,c:  16.097235  ,loss:  9.456114

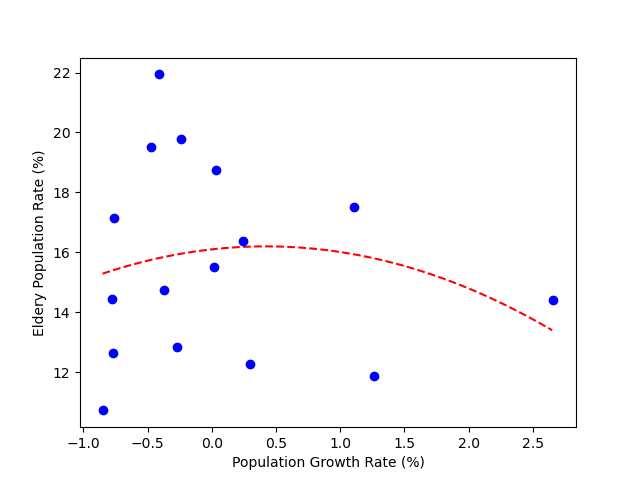
다중회귀모델

위의 코드와 같은 방식을 가리켜, 저수준 API 를 활용한 방식이라고 부르며, 라이브러리 등에서 제공해주는 함수를 사용하는 것이 아닌 직접 제작을 해서 사용하는 방식이라고 보면 된다.
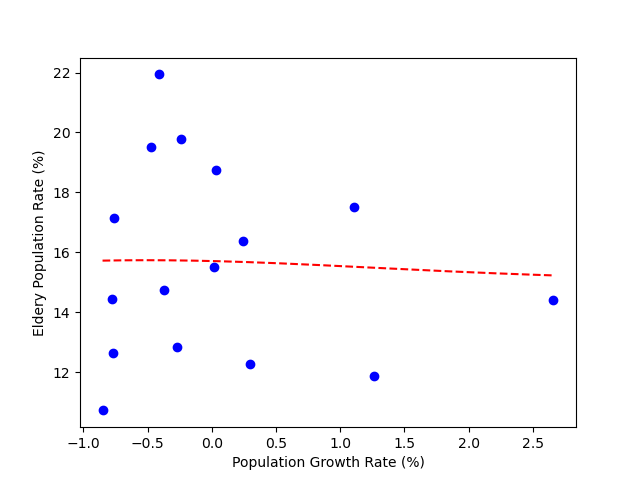
이번에는 반대로 고수준 API 방식으로 사용해서 구현해보자. 고수준 API 방식은 실제 라이브러리 및 안에 포함된 여러가지 함수들과 메소드들을 활용해서 구현하는 방식이며, 아래와 같이 구현할 수 있다.

[Python Code]

import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt

x = [0.3, -0.78, 1.26, 0.03, 1.11, 0.24, -0.24, -0.47, -0.77, -0.37, -0.85, -0.41, -0.27, 0.02, -0.76, 2.66]
y = [12.27, 14.44, 11.87, 18.75, 17.52, 16.37, 19.78, 19.51, 12.65, 14.74, 10.72, 21.94, 12.83, 15.51, 17.14, 14.42]

model = tf.keras.Sequential([
    tf.keras.layers.Dense(units=6, activation='tanh', input_shape=(1,)),
    tf.keras.layers.Dense(units=1)
])

model.compile(optimizer=tf.keras.optimizers.SGD(lr=0.1), loss='mse')
model.summary()

model.fit(x, y, epochs=10)
model.predict(x)

line_x = np.arange(min(x), max(x), 0.01)
line_y = model.predict(line_x)

plt.plot(line_x, line_y, 'r--')
plt.plot(x, y, 'bo')
plt.xlabel('Population Growth Rate (%)')
plt.ylabel('Eldery Population Rate (%)')

[실행결과]

Model: "sequential_2"
_________________________________________________________________
Layer (type)                 Output Shape              Param #
=================================================================
dense_4 (Dense)              (None, 6)                 12
_________________________________________________________________
dense_5 (Dense)              (None, 1)                 7
=================================================================
Total params: 19
Trainable params: 19
Non-trainable params: 0
_________________________________________________________________

Epoch 1/10
1/1 [==============================] - 0s 0s/step - loss: 261.4496
Epoch 2/10
1/1 [==============================] - 0s 0s/step - loss: 98.8627
Epoch 3/10
1/1 [==============================] - 0s 0s/step - loss: 12.6620
Epoch 4/10
1/1 [==============================] - 0s 0s/step - loss: 9.9969
Epoch 5/10
1/1 [==============================] - 0s 1ms/step - loss: 9.8173
Epoch 6/10
1/1 [==============================] - 0s 1ms/step - loss: 9.7966
Epoch 7/10
1/1 [==============================] - 0s 0s/step - loss: 9.7837
Epoch 8/10
1/1 [==============================] - 0s 0s/step - loss: 9.7716
Epoch 9/10
1/1 [==============================] - 0s 1ms/step - loss: 9.7596
Epoch 10/10
1/1 [==============================] - 0s 0s/step - loss: 9.7479

다중회귀모형 텐서플로

2. 텐서플로 추정기

여기서 말하는 추정기란, 계산그래프 생성, 변수 초기화, 모델 훈련, 체크 포인트 저장, 텐서보드 파일 로깅과 같은 모든 활동을 처리하는 역할을 의미하며, 텐서플로에서는 추정기를 상위 레벨의 API로 제공해주기 때문에, 이를 통해 확장 가능하고, 생산 지향적인 솔루션을 제공한다.

1) 추정기 종류

텐서플로에서 제공하는 추정기의 종류로는 기성 추정기와 맞춤형 추정기가 존재하며, 각각에 대한 설명은 다음과 같다.

① 기성 추정기
텐서플로 추정기 모델 중 하나로, 미리 작성된 추정기 모델이다. 사전에 생성된 모델이기 때문에 단순히 입력 특징만 전달하면 바로 사용 가능하다.

② 맞춤형 추정기
텐서플로 케라스에 구축된 모델에서 자신에게 맞는 추정기를 생성할 수 있다. 때문에 사용자 정의 추정기 라고도 부른다.

2) 추정기의 구성요소

텐서플로 추정기를 사용하려면, 먼저 추정기 파이프라인의 2가지 주요 구성요소를 먼저 알아야한다. 내용은 다음과 같다.

(1) 특징 열

텐서플로2.x 버전에서 등장하는 feature_column 모듈은 입력 데이터와 모델간의 가교 역할을 해준다. 이 때, 훈련을 위한 추정기가 사용하는 입력 매개 변수를 가리켜 특징 열이라고 부른다. 이러한 매개변수는 텐서플로의 feature_column 에서 정의되고 모델에서 데이터를 해석하는 방법을 지정한다.
특징 열을 생성하려면 tensorflow.feature_column 에서 아래 9가지의 함수들 중 하나를 호출해서 사용해야한다. 각 함수와 그에 대한 설명은 다음과 같다.

함수	설명
categorical_column_with_identity	각 범주는 원 핫 인코딩 되어, 공유한 ID를 갖는다. 숫자 값에만 사용할 수 있다.
categorical_column_with_vocabulary_file	범주형 입력은 문자열이고, 그에 대한 범주가 파일로 제공될 때 사용한다. 문자열은 먼저 숫자 값으로 변환된 후, 원 핫 인코딩을 수행한다.
categorical_column_with_vocabulary_list	범주형 입력은 문자열이고, 그에 대한 범주가 리스트로 정의되는 경우에 사용한다. 문자열은 먼저 숫자 값으로 변환된 후, 원 핫 인코딩을 수행한다.
categorical_column_with_hash_bucket	범주 수가 매우 많아 원 핫 인코딩이 불가능할 때, hash를 사용한다.
crossed_column	2개의 열을 병합해 하나의 특징으로 사용하고자 할 때 사용하며, 지정학적 위치를 예로 들면, 위도와 경도를 합쳐 하나의 좌표로 사용하는 것을 들 수 있다.
numeric_column	특징이 수치형인 경우에 사용하는데, 단일 숫자 혹은 행렬의 형태도 사용 가능하다.
indicator_column	직접적으로 사용하지 않지만, 범주형 컬럼과 함께 사용되는 데, 이 때 범주 수에 제한이 있고, 원 핫 인코딩으로 표시할 수 있는 경우에만 사용한다.
embedding_column	직접적으로 사용하지 않지만, 범주형 컬럼과 함께 사용하며, 이 때 범주 수가 매우 많고, 원 핫 인코딩으로 표시할 수 없는 경우에만 사용한다.
bucketized_column	특정 수치 값 대신 값에 따라 데이터를 서로 다른 범주로 분류하는 경우에 사용한다.

위의 6가지 함수는 Categorical Column 클래스에서 상속을 받고, 다음 3개 함수는 Dense Column 클래스에서, 마지막 함수는 2개 클래스 모두에서 상속받는다.

Twitter Facebook LinkedIn

김길현

[Python Deep Learning] 2. 회귀 (Regression)

1. 회귀

1) 단순 선형 회귀

2) 다중 선형 회귀

2. 텐서플로 추정기

1) 추정기 종류

2) 추정기의 구성요소

(1) 특징 열

공유하기

댓글남기기

참고

[Review] 2. WIS 2023 후기

[Spring] 18. RestTemplate 사용하기 Ⅱ : Post 방식

[Spring] 17. RestTemplate 사용하기 Ⅰ : Get 방식

[Spring] 16. Spring Interceptor