[Python Deep Learning] 17. 문장을 표현하는 방법

0. 들어가며

앞선 장 까지는 Token 을 이용한 표현(Token representation) 에 대해 알아봤다. 간단하게 정리해보자면, 신경망의 입장에서는 첫번째 노드를 지나면, 문장은 특정 단어(토큰)의 벡터로 바뀌게 되며, 각 벡터들은 갖고 있는 토큰마다 어떠한 의미를 갖고 있으며, 이를 이용해 계산을 해서 나오는 결과 벡터는 카테고리의 개수와 동일하며, 그래야만 softmax 활성화 함수를 통해 분류 가능한 형태로 나오게 될 것이다. 때문에 사실상 카테고리 분포로 다중 클래스 분류를 하는 것과 유사하다고 볼 수 있다. 하지만, 문장의 경우에는 길이가 고정되어 있지 않으며, 짧은 문장도 있고, 긴 문장도 존재할 수 있다. 이처럼 입력의 길이가 바뀌는 경우에는 어떻게 고정된 길이의 표현법을 찾을 수 있을지를 이번 장에서 살펴보도록 하자.

1. CBOW 기반의 텍스트 다중 분류 모델

가장 간단한 방법이라고 한다면, 앞선 장에서 봤던 CBOW 기법일 것이다. 이는 토큰 순서가 어떻든, 관계없이 bag 으로 보겠다는 의미이며, 어떤 단어가 들어가 있는가가 중요하다는 의미이다.

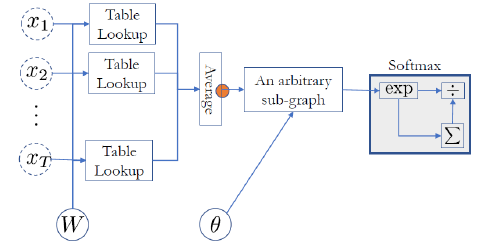
예를 들면 위의 그림과 같이 각 단어, 토큰들이 이미 table lookup 을 통해서 벡터 형태로 바뀌었다고 가정해보자. 이제 벡터로 변환된 값을 이용해 averaging 한다고 가정해보자. average 하는 것도 하나의 노드이며, 말이 averaging 이지, sum을 하는 것이기 때문에 자코비안 계산도 간단하다. 다시 돌아와서 각 벡터를 고차원으로 이동시켜서 본다면, 점으로 존재하게 될 것이다. 그리고 이 점들의 average point 가 어디 있는지 찾는 것이 목표이며, 해당 포인트가 곧 문장을 의미한다고 볼 수 있다. 그렇다면 이를 CBOW 로 어떻게 가능할까? 사실 CBOW 기법은 일반화를 하면 Continuous Bag-of-N-gram 으로 볼 수 있다. 때문에 토큰 하나만으로 의미 파악이 부족하다면, 2개 씩 묶어서 보는 시도도 가능하다는 것이다. 위와 같이 할 경우, 장점은 CBOW 는 순서를 무시함에도 성능이 좋다는 점이다. 즉, 텍스트 분류와 같은 문제에서 CBOW를 사용하고, 그 뒤에 layer를 추가해서 분류 모델을 만들면 성능이 좋은 편이다. 결과적으로 다음과 같이 과정에 대해 정리할 수 있다.

[CBOW 기반 텍스트 분류 모델 동작 과정]
1. 입력된 문장을 토큰 단위로 나눈다.
2. 각 토큰에 대해서 동일한 가중치로 table lookup 하는 과정을 거친다 (Word Embedding)
   해당 과정을 거친 토큰들은 모두 벡터 형태로 변환된다.
3. averaging 노드를 이용해 전체 averaging 한다.
   이 과정을 통해 도출된 결과는 입력 문장에 대한 표현값이 된다.
   그리고 이 값은 representation space 내에서 비슷한 의미를 가진 문장들은 가까운 위치에 있으며,
   다른 의미를 가진 문장은 멀리있는 형태가 된다. (텍스트 분류 하기 좋은 상태임)
4. representation 된 벡터를 이 후에 구성해 둔 분류모델을 통과시키고, softmax 활성화함수를 통과하면,
   전체에 대한 분류 결과가 나오게 된다.

2. Relation Network

다음으로 알아볼 방법은 Relation Network 기법이다. 단어에 Network 라는 단어가 포함되었지만, 사실상 Skip Bigram 기법이라고 봐도 된다. 여기서 Bigram 이란, 단어나 토큰이 2개가 나란히 있을 때를 말한다. 이 또한 의미가 Bigram 이지만, 꼭 나란히 있는 2개의 토큰일 필요는 없고, 띄엄띄엄 볼 수도 있다. 해당 기법은 문장 내의 모든 단어간의 관계를 계산하지만, 이 때 자기자신은 제외하고 계산하게 된다. 때문에 특정 문장이 주어졌을 때, 단어들은 x1, …. , xt 와 같이 주어졌을 때, 모든 pair case 에 대해서 신경 쓰며, 모델의 구조는 다음과 같이 나타낼 수 있다.

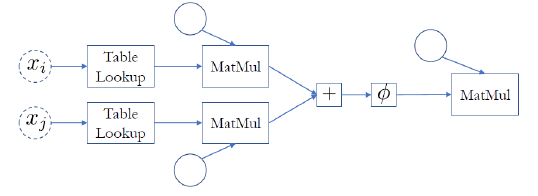
위의 모델에서 학습에 사용되는 가중치는 “Dense layer의 가중치 + 이전에 주어진 가중치” 로 계산된다. 그리고 앞서 언급한 모든 pair case 에 대한 표현은 다음과 같다.

$ f(x_i, x_j) = W_{\Phi }(U_{left} e_i + U_{right} e_j)$

모든 pair case가 위의 수식과 같을 때, 최종적으로 Relation Network 를 통해 계산되는 관계에 대한 값은 다음과 같다.

$RN(X) = \frac{1}{2N(N-1)} \sum _{i=1}^{T-1} \sum _{j=i+1}^Tf({x}_i,\ {x}_j)$

위의 수식들을 이용해서, 앞서 본 Relation Network 그림을 좀 더 세부적으로 표현해보자면, 다음과 같이 나타낼 수 있다.

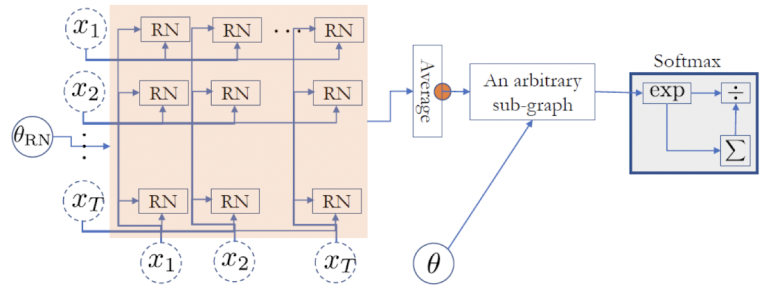
이처럼 여러 개의 단어를 pair로 구성함으로써, 단어들 간의 관계를 통해 전체적인 문장에 대한 분류를 할 수 있다.

3. CNN 을 이용한 N-gram 방식: K-grams

세번째로 알아볼 방법은 CNN 을 응용해서 텍스트 분류를 하는 방법이다. 갑자기 영상처리에서 사용되는 CNN 으로 뭘하겠다는 것인지 의문이 들 수도 있다. 우선 이 기법의 아이디어는 계층적으로 N-gram 방식을 적용하겠다는 점이다. 우선, 우리가 워드 임베딩을 통해 토큰을 벡터화하게되면, 수치형으로 변경된다는 것은 알고있다. 그리고 앞서 영상처리에서 배운것처럼 CNN은 필터를 통해 수용영역 만큼의 데이터에서 특징을 찾아내는 방식으로 학습을 진행한다. 이 2가지를 응용해서 보면, 아래 그림과 같이 벡터화된 토큰들을 계층적으로 연관지어 K-gram 방식으로 학습한다는 점이다. 여기서 K 값은 커널의 크기를 의미한다.

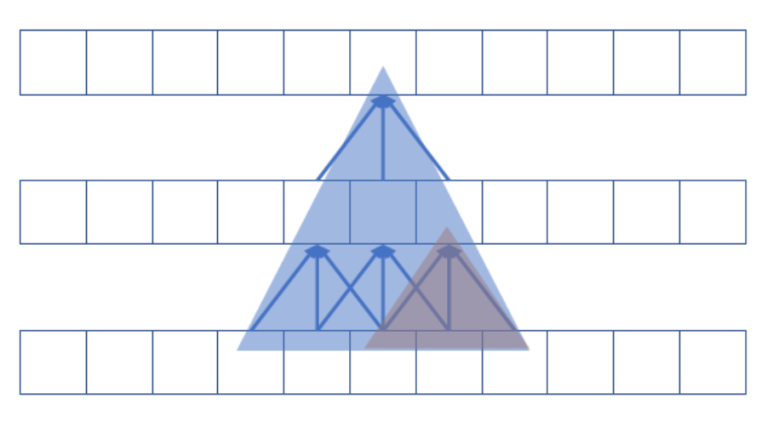
이 때는 모든 토큰간의 관계를 확인해야되므로, 1D-Conv. layer를 사용한다. 또한 앞선 설명에서는 하나의 벡터화된 토큰에 대해 다음 문장의 벡터화된 토큰들 간의 N-gram을 구성한다고 했지만, 이를 여러 개의 1D-Conv. layer로 이어주면, 점진적으로 확장하는 윈도우를 구성할 수 있다. 뿐만 아니라, Conv. layer 자체가 필터로서의 역할도 제공해주기 때문에, 컨볼루션 레이어의 장점 상 입력 데이터에 대한 특징을 더 잘 찾아주는 효과도 기대할 수 있다. 하지만, 중요한 특징이 서로 먼 거리에 있다고 가정하면, 이를 찾기 위해 컨볼루션 레이어를 여러 개 쌓아야하고, 그렇게 되면, 모델 자체가 커지게 되어, 학습도 느려질 수 있다는 단점이 있다.

4. Self Attention

앞서 우리는 Relation Network(RN) 와 CNN 을 사용한 N-gram 방식까지 살펴봤다. 요약해보자면, RN은 전체적인 토근에 페어를 만들어 비교하는 식으로 문장을 표현하고, CNN 은 일정부분의 토큰에 페어를 만들어 비교하는 식으로 문맥에 대해서만 초점을 두는 방식이다. 하지만, 우리는 문장의 길이만큼 보지만, 그렇다고 전체를 보는 것이 아니라 중요 부분만 확인하면 된다. 그렇다면, 이 둘을 적절하게 섞으면 어떻게 될까? 위의 2가지 기법의 장점만을 섞어 고안한 방식이 바로 지금부터 다룰 Self Attention 이라는 방식이다. Self Attention 방식은 앞선 2가지 기법의 Super Set 에 마스킹 된 벡터(입력 벡터에 대한 반전)을 곱해서 더하는 방식이다. 원리를 설명하기 위해, 먼저 RN의 가중치 계산법과 CNN 의 가중치 계산법을 비교해보자.

$ RN: h_t = f(x_t, x_1) + … + f(x_t, x_{t-1}) + f(x_t, x_{t-1}) + … + f(x_t , x_T) $

$ CNN: h_t = f(x_t, x_{t-k}) + … + f(x_t, x_t) + … + f(x_t , x_{t+k})$

다음으로 RN에서의 방식대로 CNN의 가중치를 계산한다면 아래와 같이 식으로 표현할 수 있을 것이다.

$본래 가중치계산: h_t = f(x_t, x_{t-k}) + … + f(x_t , x_t) + … + f(x_t , x_{t+k}) $

$변형 가중치계산: h_t = \sum_{t’=1}^T \prod (\vert {t’-t} \vert \leq k)f(x_t , x_{t’}) (S가 참이면,\prod (S)=1 , 아니면 0) $

위와 같이 가중치 계산 방식을 바꿨을 때, 이를 0 ~ 1로 고정하지 않고 가중치를 계산할 수 있을까? 이를 가능하게 하려면, 각 pair 별로 가중치를 적용하는 것이다. 이를 식으로 표현하면 다음과 같다.

$h_t = \sum_{t’=1}^T \alpha (x_t, x_{t’}) f(x_t , x_{t’})$

위의 수식에서 $ \alpha(x_t , x_{t’}) $ 부분은 RN에서 사전에 학습된 가중치를 사용하기 때문에, 다음과 같이 표현할 수 있다.

$ \alpha (x_t , x_{t’}) = \sigma (RN(x_t , x_{t’})) \in [0, 1]$

$ \alpha (x_t , x_{t’}) = \frac {\exp (\beta (x_t , x_{t’}))}{\sum_{t’=1}^T \exp (\beta (x_t, x_{t’}))}, (단, \beta (x_t , x_{t’})=RN(x_t, x_{t’}) 일 때)$

결과적으로 Self Attention 은 앞서 언급한 것처럼 CNN 과 RN 의 장점만을 사용한 방법이다. 위에서 볼 수 있듯이, 기존에 RN 만으로 할 때, 중요 단어간의 거리가 먼 경우에 학습이 어렵다는 단점을 해결하였으며, 문장의 길이에 상관없이 학습이 가능하다는 점을 해결했다. 하지만, 기존의 RN 이 갖는 단점을 해결한 만큼, 문장이 들어오면, 전체 토큰에 대해 가중치를 계산하고, 계산된 결과를 Matmul 연산으로 통합(Merge) 해주기 때문에 계산량이 많이 든다는 단점이 있다.
위의 문제를 해결하기 위해서 등장한 것이 RNN을 활용한 Attention 이며, 현재 자연어 처리, 특히 기계 번역 등에서 많이 사용되는 Transformer 의 시초가 된다.

[참고자료]
https://wikidocs.net/21995 https://junklee.tistory.com/43