[Python Deep Learning] 15. LSTM

1. 개요
앞서 우리가 배운 RNN은 한 가지 단점이 있다. 앞선 장에서도 언급했듯이, 입력 데이터가 길어질 수록 학습능력이 떨어진다는 점이다. 이를 가리켜 장기 의존성(Long Dependency) 의 문제라고 한다. 입력 데이터와 출력 사이의 길이가 멀어질 수록 연관 관계가 적어지며, 현재의 답을 얻기 위해 과거의 정보에 의존해야하는 RNN이지만, 과거 시점이 현재와 너무 멀기 때문에 문제를 해결하기 어려워지는 것이다.
이러한 장기 의존성 문제를 해결하기 위해 1997년에 LSTM (Long Short Term Memory)이 등장하게 된다.
2. LSTM (Long Short Term Memory)
LSTM의 구조를 살펴보기 전에 RNN의 구조를 간단하게 짚고 넘어가보자. 앞선 장의 내용을 살펴보면, t 시점에서 입력 x와 이전 시점의 출력인 ht-1 을 합친 후, 활성화함수 tanh 를 통과하고, 출력 ht 를 다음 시점 방향과 출력방향으로 값을 출력한다. 그림은 다음과 같다.
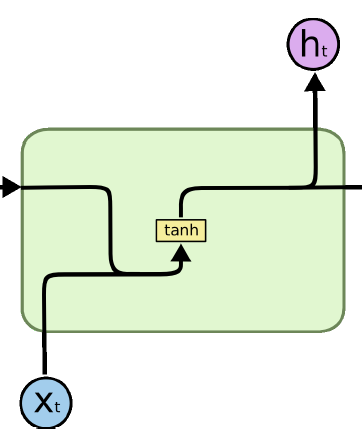
이에 비해 LSTM은 아래 그림과 같이 셀의 형태로 나타나며, RNN에 비해 다소 복잡한 모양을 갖는다.
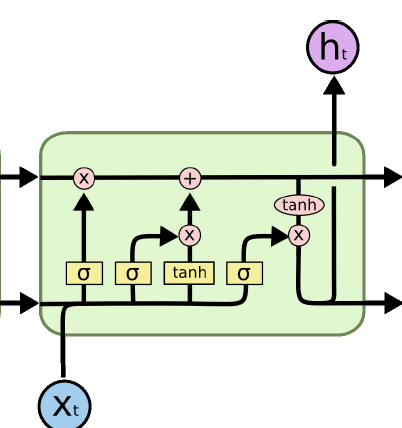
위의 그림을 봤을 때, 가장 큰 차이점을 말하자면, 시점 방향으로 각 셀의 상태인 ci 과 이전 셀에서의 가중치인 ht 를 같이 전달한다. 다음으로 RNN에는 없었지만, 내부적으로 Gate 및 State 에 대한 노드들이 생겼다. 구체적인 내용은 다음과 같다.
1) 구조
앞서 언급한 것처럼 LSTM에는 3개의 Gate 와 2개의 State 가 존재한다. 각 노드들에 대한 설명은 다음과 같다.
(1) Forget Gate
가장 먼저 살펴 볼 Forget Gate 는 기억을 잊고자 하는 정도를 나타낸다. 활성화함수로 시그모이드(Sigmoid) 함수를 사용하며, 출력값이 0 ~ 1 사이의 값을 갖는다. 특징이 여러 차원으로 되어 있기 때문에, 결과적으로 특징별로 기억할 지의 여부를 결정한다.
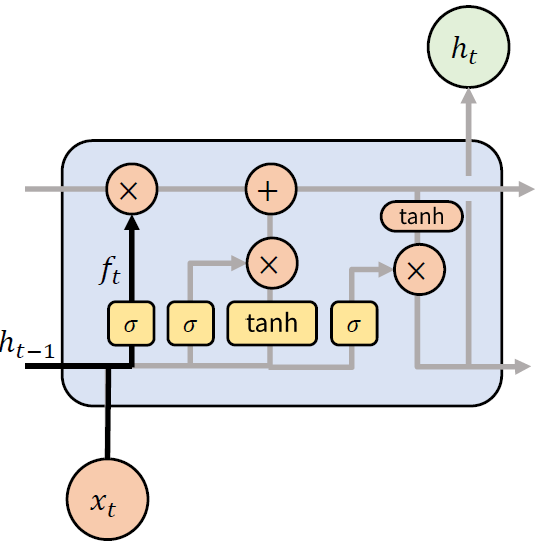
위의 내용을 수식으로 표현하면 다음과 같다.
$ f_t = \sigma (W_{xf} x_t + W_{hf} h_{t-1} + b_f) $
(2) Input Gate
다음으로 볼 Input Gate 는 새로운 입력을 받고자 하는 정도를 나타낸다. Forget Gate와 동일하게 시그모이드 함수를 활성화함수로 사용하며, 특징이 여러 차원으로 되어 있기 때문에, 특징별로 받아들일지 말지를 결정한다.
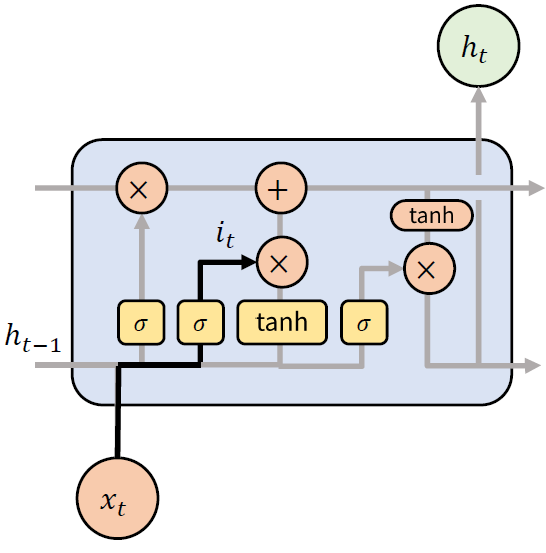
이를 수식으로 표현하면 다음과 같다.
$ i_t = \sigma (W_{xi} x_t + W_{hi} h_{t-1} + b_i) $
(3) Output Gate
Output Gate 는 Cell State 중에서 어떤 특징을 출력할 지에 대해 결정한다. 앞선 Gate 들과 동일하게 시그모이드 함수를 활성화 함수로 사용한다.
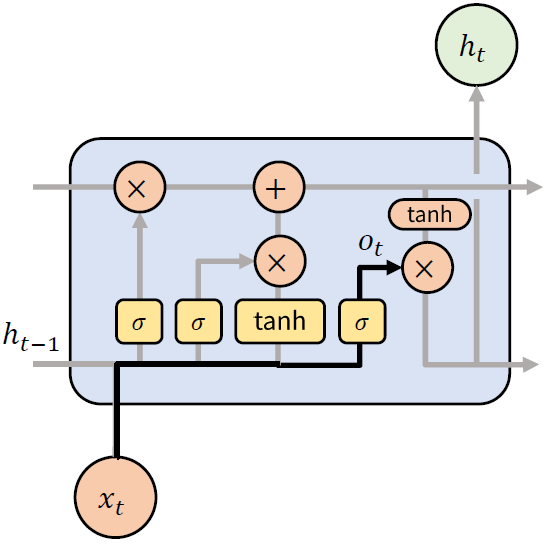
수식으로 나타내면, 다음과 같다.
$o_t = \sigma (W_{xo} x_t + W_{ho} h_{t-1} + b_o) $
(4) Cell State
Cell State는 메모리 역할을 한다. 여러 차원으로 되어있어, 각 차원은 특정 정보를 기억한다. 때문에, 특징별로 기억하거나, 잊거나, 새로운 정보를 받을 수 있다.
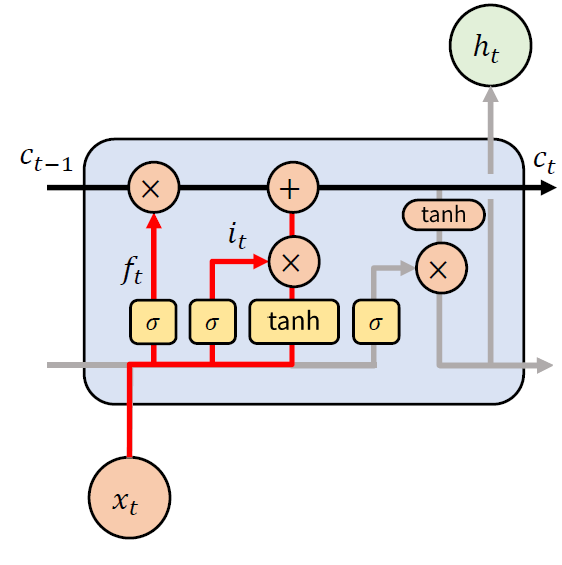
수식으로 표현하면, 다음과 같다.
$ f_t = \sigma (W_{xf} x_t + W_{hf} h_{t-1} + b_f) $
$ i_t = \sigma (W_{xi} x_t + W_{hi} h_{t-1} + b_i) $
$ g_t = \tanh (W_{xg} x_t + W_{hg} h_{t-1} + b_g) $
$ c_t = f_t \odot c_{t-1} + i_t \odot g_t $
(5) Hidden State
마지막으로, Hidden State 는 Cell State 에 하이퍼볼릭 탄젠트(tanh) 함수를 활성화 함수를 적용한 후, Output Gate 로 선별해서 출력한다. 활성화 함수로 하이퍼볼릭 탄젠트 함수를 사용한 이유는 그림을 통해 알 수 있듯이, Cell State 값이 계속 누적되는 것을 확인할 수 있는데, 시간이 지날 수록 값이 커지게 되고, 이로 인한 그레디언트 값도 점차적으로 커지게 되어, 그레디언트 폭주(Gradient Explode)현상이 발생할 수 있다. 이를 억제하고자 출력 값의 범위가 -1 ~ 1 사이로 나오도록 설정하기 위함이다.
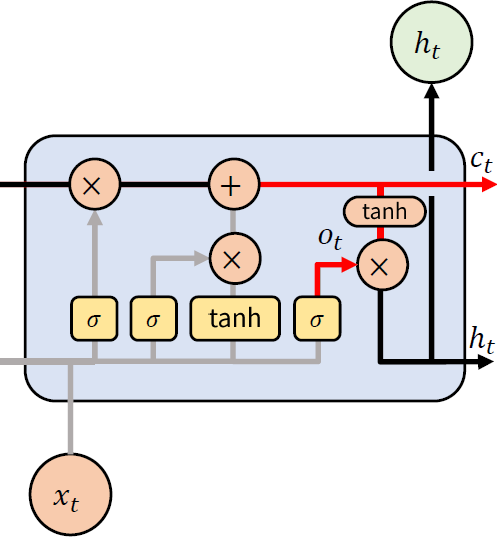
수식으로 표현하자면, 아래와 같이 나타낼 수 있다.
$ o_t = \sigma (W_{xo} x_t + W_{ho} h_{t-1} + b_o) $
$ h_t = o_t \odot \tanh (c_t) $
2) 동작 원리
앞서 살펴본 구조를 좀 더 길게 보자면, 아래 그림과 같이 사슬 형태로 연결되어 있다는 것을 확인할 수 있다.
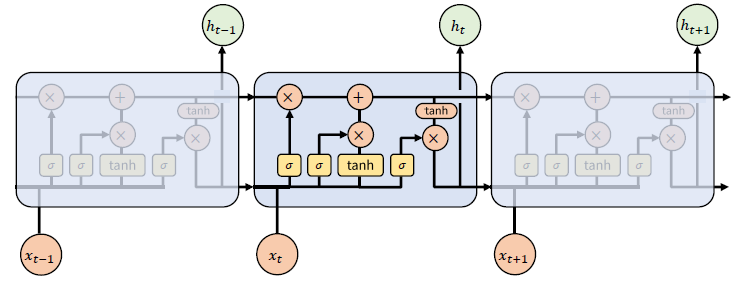
LSTM 순환신경망이 동작하는 원리는 다음과 같다.
[LSTM 동작원리]
1. Forget Gate 를 통해 이전 특징 별로 기억 여부를 결정한다.
2. Input Gate 를 통해 현 시점의 정보가 얼마나 중요한 지를 반영하여 기록한다.
3. 이전 Cell State의 결과와 현 시점의 Forget Gate에서 잊고, Input Gate의 중요도만큼 곱한 값을 합쳐, 현 시점의 메모리 셀(Memory Cell) 값을 생성한다.
4. 현 시점의 Forget Gate, Input Gate 에 의해서 변경된 현 시점의 Cell State 값을 얼마만큼 다음 레이어로 전달할 지를 계산한다.
3) 한계점
순수 RNN 보다 개선된 모델이 LSTM 이긴 하지만, 파라미터가 많고 복잡하다는 단점이 있다. 뿐만 아니라, Gate를 통해 연산된 결과를 곱해서 0 ~ 1 사이의 값으로 비선형성을 주기 때문에, 굳이 별도의 활성화 함수를 사용할 필요는 없을 수도 있다.
3. 구현하기
끝으로, 앞서 RNN에서 본 Hello 를 학습해보는 예제를 실습해보면서, 간단한 LSTM 모델을 생성해보도록 하자.
시작하기에 앞서, 실습에 사용할 데이터를 먼저 생성해주도록 하자.
[Python Code]
import os
import numpy as np
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
from tensorflow.keras.utils import to_categorical
import matplotlib.pyplot as plt
# One-Hot Encoding
h = [1, 0, 0, 0]
e = [0, 1, 0, 0]
l = [0, 0, 1, 0]
o = [0, 0, 0, 1]
x_data = np.array([[h, e, l, l, o],
[e, o, l, l, l],
[l, l, e, e, l]], dtype=np.float32)
RNN 계열의 모델에서는 hidden_size, sequence, one-hot vector 를 사용하기 때문에 3차원으로 구성해야한다. 그렇기 때문에 x_data 의 형태가 얼핏 보면 2차원으로 보일 수 있지만, One-Hot 인코딩의 결과를 반영하게되면, 3차원의 데이터가 생성되는 것이다.
다음으로 LSTM 모델을 만들어보자. 이번 예제에서는 간단하게 LSTM 셀 1개만 사용할 예정이며, 텐서플로의 케라스에서 함수로 제공해준다. 그리고 모델에 대한 출력은 output, 은닉 상태, 셀 상태 순으로 반환해준다.
[Python Code]
# 간단하게 LSTM 모델 생성
rnn = layers.LSTM(units=2, return_sequences=False, return_state=True)
outputs, h_states, c_states = rnn(x_data) # 출력 결과 순서 : outputs, hidden_states, cell_states
print('x_data: {}, shape: {} \n'.format(x_data, x_data.shape))
print('outputs: {}, shape: {} \n'.format(outputs, outputs.shape))
print('hidden_states: {}, shape: {}'.format(h_states, h_states.shape))
print('cell_states: {}, shape: {}'.format(c_states, c_states.shape))
[실행 결과]
x_data: [[[1. 0. 0. 0.]
[0. 1. 0. 0.]
[0. 0. 1. 0.]
[0. 0. 1. 0.]
[0. 0. 0. 1.]]
[[0. 1. 0. 0.]
[0. 0. 0. 1.]
[0. 0. 1. 0.]
[0. 0. 1. 0.]
[0. 0. 1. 0.]]
[[0. 0. 1. 0.]
[0. 0. 1. 0.]
[0. 1. 0. 0.]
[0. 1. 0. 0.]
[0. 0. 1. 0.]]], shape: (3, 5, 4)
outputs: [[ 0.14071466 -0.06253189]
[ 0.23642766 0.11880982]
[ 0.21439378 0.20815167]], shape: (3, 2)
hidden_states: [[ 0.14071466 -0.06253189]
[ 0.23642766 0.11880982]
[ 0.21439378 0.20815167]], shape: (3, 2)
cell_states: [[ 0.32512775 -0.10648637]
[ 0.74161536 0.2519838 ]
[ 0.6292345 0.46296534]], shape: (3, 2)
함수 사용법에 대한 자세한 내용은 텐서플로 공식 홈페이지에서 확인이 가능하니 참고바란다. 또한 RNN 계열의 모델을 사용하기 위해서는 단어 임베딩(Word Embedding) 을 한 후에, 모델에 대한 학습이 가능하며, 관련된 내용은 추후에 다룰 예정이며, 좀 더 복잡한 자연어처리와 관련된 예제는 해당 내용과 함께 다룰 예정이므로, 이번 예제의 실습은 여기서 마무리하겠다.

댓글남기기