[Python Deep Learning] 14. RNN

1. 언어모형
자연어 처리나 언어 번역등에 사용되는 언어 모형은 주로 다음으로 올 단어를 예측하는 문제를 해결하기 위해서 만들어진다. 일반적이라면, 다음으로 이미 주어진 단어 시퀀스를 통해 다음으로 올 단어들의 확률을 계산하는 방식으로 연산한다. 다른 유형의 언어 모델로는 주어진 양쪽의 단어들로부터 가운데 비어있는 단어를 예측하는 모델도 있다. 마치 영어문제 중에 문장 중 일부를 빈 칸으로 하고 들어갈 말이나 단어를 찾는 것과 유사하다. 언어 모형은 주로 기계 번역이나, 오타 교정, 음성인식, 검색엔진 등에서 많이 활용된다.
2. 통계적 언어 모델
1) 조건부 확률
조건부 확률은 두 확률 P(A) 와 P(B)에 대해 다음과 같은 관계를 갖는다. 수식으로 표현하면, 다음과 같다.
$ p(B \mid A) = \frac {p(A, B)} {p(A)} $
$ P(A, B) = P(A)P(B \mid A) $
예를 들어 4개의 확률에 대한 조건부 확률을 계산하자면 다음과 같다.
$ P(A, B, C, D) = P(A)P(B \mid A)P(C \mid A, B)P(D \mid A, B, C) $
위와 같이 표현된 것을 조건부 확률의 연쇄법칙(Chain rule) 이라고 한다. 위의 식은 4개였다면, 이를 일반화한다면, 다음과 같이 표현할 수 있다.
$ P(x_1, x_2, x_3, … , x_n) = P(x_1)P(x_2 \mid x_1)P(x_3 \mid x_1, x_2) … P({x_n} \mid {x_1…} x_{n-1}) $
2) 문장에 대한 확률
그렇다면 어떻게 사용되는 지 알아보도록 하자. 예를 들어, 문장 ‘An adorable little boy is spreading smiles’ 의 확률인 를 식으로 표현해보자.
각 단어는 문맥이라는 관계로 인해 이전 단어의 영향을 받아서 나온 단어들이다. 그리고 모든 단어로부터 하나의 문장이 완성된다. 앞서 언급한 조건부 확률의 일반화식을 문장의 확률 관점에서 구성해보자면 다음과 같이 나타낼 수 있다.
$ P(An\ \ adorable\ \ little\ \ boy\ \ is\ \ spreading\ \ smiles) = P(An)P({adorable} \mid {An})P({little} \mid {An\ \ adorable})P({boy} \mid {An\ \ adorable\ \ little})P({is} \mid {An\ \ adorable\ \ little\ \ boy})P({spreading} \mid {An\ \ adorable\ \ little\ \ boy\ \ is})P({smiles} \mid {An\ \ adorable\ \ little\ \ boy\ \ is\ \ spreading}) $
3) 카운트 기반의 접근
문장의 확률을 구하기 위해서 다음 단어에 대한 예측확률을 모두 곱한다는 것을 알아봤다. 그렇다면 통계적 언어 모델은 이전 단어로부터 다음 단어에 대한 확률의 계산은 어떻게 구할까? 예를 들어 An adorable little boy 가 나왔을 때, 다음 단어로 is 가 나올 확률을 계산해보자.
$ P({is} \mid {An\ \ adorable\ \ little\ \ boy}) = \frac {count(An\ \ adorable\ \ little\ \ boy\ \ is)} {count(An \ adorable \ \ little \ \ boy)} $
| 예를 들어, An adorable little boy 가 100 번 등장했는데 그 다음에 is 가 나온 경우가 30번이라고 가정한다면, P(is | An\ \ adorable\ \ little\ \ boy) 는 30% 가 된다. |
3. N-gram 언어 모델
N-gram 모델은 일종의 통계적 언어 모델 중 하나로, 임의의 개수를 정하기 위한 기준을 위해 사용하는 모델이다. 코퍼스에서 n 개의 단어 뭉치 단위로 끊어서 이를 하나의 토큰으로 간주한다. 예를 들어, 문장 An adorable little boy is spreading smiles 가 있을 때, 각 n에 대해서 n-gram을 전부 구하면, 다음과 같다.
[N-gram]
unigrams (n=1)
- an, adorable, little, boy, is, spreading, smiles
bigrams (n=2)
- an adorable, adorable little, little boy, boy is, is spreading, spreading smiles
trigrams (n=3)
- an adorable little, adorable little boy, little boy is, boy is spreading, is spreading smiles
4-grams (n=4)
- an adorable little boy, adorable little boy is, little boy is spreading, boy is spreading smiles
n-gram을 통한 언어 모델에서는 다음에 날올 단어의 예측은 오직 n-1개의 단어에만 의존한다. 즉, 4-grams 이고, “An adorable little boy is spreading” 다음에 나올 단어를 예측한다하면, 사실 “boy is spreading” 3개의 단어만 고려하게 된다. 따라서 위의 문장 다음에 나올 단어의 확률을 계산하면 다음과 같다.
$ P(w \mid {boy\ \ is\ \ spreading}) = \frac {count(boy\ \ is\ \ spreading\ \ w)} {count(boy\ \ is\ \ spreading)} $
위와 같을 때, boy is spreading 이 1000번 등장했다하자. 그리고 boy is spreading insults 가 400번, boy is spreading smiles 가 200번이라고 하면, insults가 등장할 확률은 50%, smiles가 등장할 확률은 20%가 된다.
이러한 n-gram 모델도 한계점은 있다. 코퍼스 데이터를 어떻게 가정하느냐의 나름이고, 전혀 말이 안되는 문장은 아니나, 일부 단어 몇 개만 보다보니 의도하고 싶은 데로 문장을 끝맺지 못할 수도 있다는 한계점이 있다.
4. RNN (Recurrent Neural Network)
앞서 살펴 본 통계적 언어모델을 개선하기 위해서 등장한 것이 바로 RNN 이다. RNN은 입력과 출력을 시퀀스 단위로 처리하는 시퀀스 모델(Sequence Model)이다. 대표적인 것이 바로 번역기인데, 입력은 번역하고자 하는 단어의 시퀀스인 문장이고, 출력에 해당되는 번역된 문장 또한 단어의 시퀀스이다. 이렇듯 연속된 데이터를 처리하는 모델을 시퀀스 모델이라고 하는데, RNN은 그 중 가장 기본적인 인공신경망 시퀀스 모델이다.
1) 구조
이전까지 살펴본 모델들 혹은 신경망 구조는 모두 은닉층에서 활성화 함수를 통과한 결과를 출력층 방향으로만 향하도록 설계되어 있었다. 그리고 이러한 구조를 가리켜, 피드 포워드(Feed Forward) 신경망이라고 한다. 하지만, RNN의 경우 아래 그림에서와 같이 은닉층의 노드에서 활성화 함수를 통해 나온 결과를 출력층으로 보내는 동시에 다시 은닉층 노드의 다음 입력 값으로도 보내는 특징을 갖고 있다. 그리고 이 유닛을 가리켜, 셀(Cell) 이라고 한다.
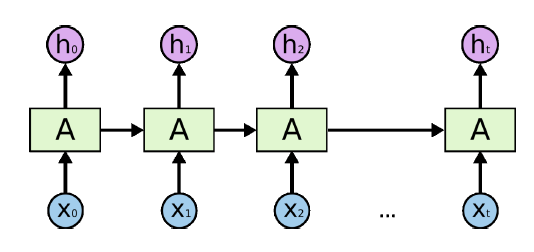
위의 구조를 통해서 알 수 있듯이, 동일한 가중치를 셀에서 다음 셀로 적용할 수 있으며, 이러한 구조를 통해 이전의 값을 기억하는 일종의 메모리 역할을 수행하기 때문에, 메모리 셀 또는 RNN 셀이라고 표현한다.
은닉층의 메모리 셀은 각각의 시점에서 바로 이전 시점에서의 은닉층 결과를 다시 입력을 사용하는 재귀적인 구조를 갖는다. 예를 들어, 현재 시점을 t라고 하고, 다음 시점인 t+1에게 보내는 값은 위의 그림상 가로선에 해당하며, 이 값을 은닉 상태(Hidden State) 값이라고 한다. 추가적으로 입력층과 출력층에서 각각 사용되는 값은 입력 벡터, 출력 벡터라는 표현을 주로 사용한다.
2) 유형
RNN은 입력과 출력의 길이를 다르게 설계할 수 있으므로 아래 그림과 같이 다양한 구조로 설계할 수 있다.
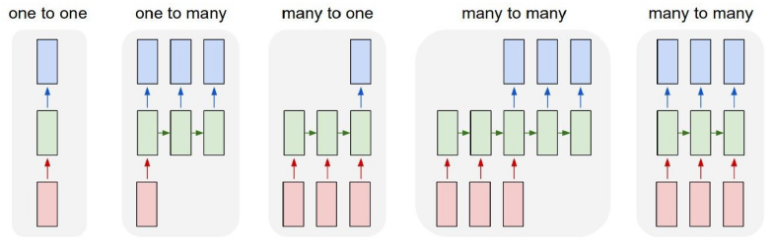
RNN 셀의 각 시점의 입, 출력 단위는 사용자가 정의하기 나름이나, 보편적으로는 단어 벡터 단위로 한다.
3) 동작 원리
(1) 순전파
다음으로 RNN의 동작원리를 알아보자. RNN에 대한 구조를 수식으로 표현하면, 다음과 같다.
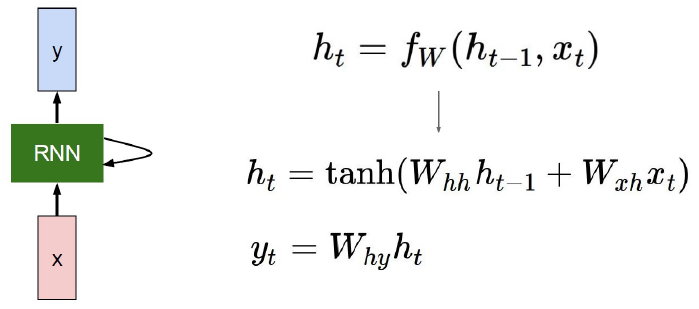
현 시점을 t라고 표현하면, 직전 시점은 t-1, 직후 시점은 t+1 로 표현할 수 있으며, 셀 별로 은닉상태는 $h_t$ 로 정의하자. 이 때 은닉상태 $h_t$ 를 계산하기 위해서는 총 2개의 가중치를 가진다. 하나는 입력층에 대한 가중치 $W_x$ 이고, 다른 하나는 이전 은닉 상태값 $h_{t-1}$ 에 대한 가중치 $W_h$ 이다. 이를 수식으로 표현한 것이 위의 그림에 나온 내용이다. 위의 수식에서는 tanh 함수를 사용했지만, 그 외에 비선형 활성화 함수 중 하나를 사용하면 된다.
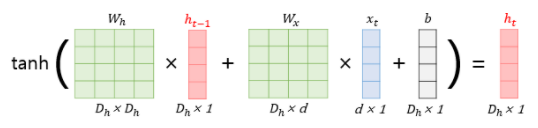
이를 행렬로 표현하자면 다음과 같다. 입력 $x_i$ 는 d 의 길이를 갖는 단어 벡터이며, 은닉 상태의 크기를 $D_h$ 라고 했을 때, 각 벡터 및 행렬의 크기는 다음과 같다.
- 입력($x_t$) : $d \times 1$
- 입력 가중치($W_x$) : $D_h \times d$
- 은닉 가중치($W_h$) : $D_h \times D_h$
- 직전 은닉 상태($h_{t-1}$) : $D_h \times 1$
- 바이어스(b) : $D_h \times 1$
위의 내용들과 활성화함수로 하이퍼볼릭탄젠트 함수를 이용해 현재 은닉상태 값인 $h_t$ 를 계산하면 다음과 같이 나타낼 수 있다.
이해를 돕기위해, “hello” 라는 단어를 학습한다고 가정하며, 입력으로는 “hell” 이라는 시퀀스가 주워지면, o 를 출력하는 모델을 만든다고 가정해보자. 이 때, 단어를 구성하는 철자는 ‘h’, ‘e’, ‘l’, ‘o’ 이며, 이를 one-hot 인코딩으로 표현하면 다음과 같다.
[hello 의 철자 one-hot 인코딩 결과]
h: 1000 e: 0100 l: 0010 o: 0001
또한 은닉층은 아래 그림과 같이 구성되고 가중치가 부여되어 있다고 가정해보자.

위의 그림에서 ‘h’ 단어가 학습할 때 사용되는 은닉층은 이전 결과가 없기 때문에 랜덤한 값으로 채워지게 된다. 어찌됬든 각 단어를 넣었을 때, 계층별로 출력된 결과가 아래의 그림과 같다고 가정해보자.
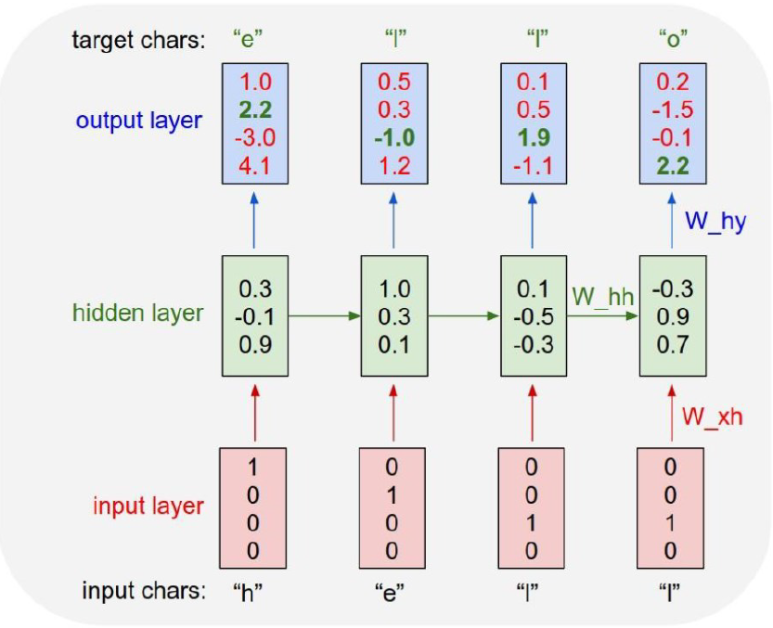
위의 그림에서 output layer의 4개 숫자가 계산된 결과이며, 숫자 중 초록색으로 표시된 부분이 정답에 해당하는 부분이다. 다른 인공신경망과 동일하게 RNN 역시 정답을 필요로 하며, 이러한 정보를 토대로 역전파를 진행하게 된다.
(2) 역전파
RNN이 학습하는 파라미터는 구조에서 볼 수 있듯이, 2가지의 가중치를 갖는다. 하나는 이전 은닉층에서 다음 은닉층으로 전달되는 가중치($W_{hh}$) 와 은닉층에서 입력층의 값으로 연산되어 출력층으로 전달하는 가중치 ($W_{hy}$) 가 해당된다.
하지만 여기서 한가지 문제가 있다. 기존 인공신경망들처럼 역전파를 하게 되면 아래 그림과 같은 현상이 발생하게 되고, 이걸 다 제대로 계산할 지도 의문이다.
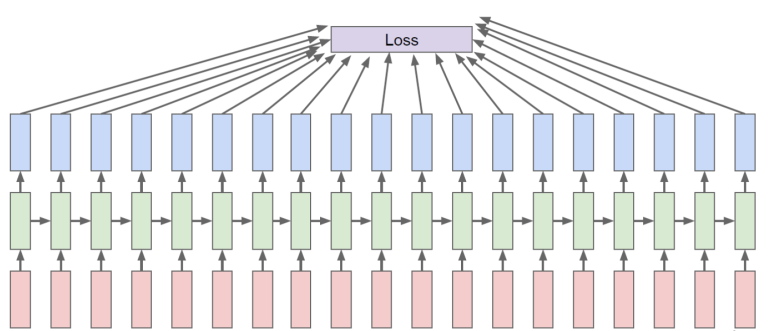
때문에, 기존의 역전파와 동일하게 하기 위해서 시간적으로 펼친 상태로 역전파를 진행한다. 이를 가리켜 시간 펼침 역전파(BPTT, BackPropagation Through Time) 이라고 부른다. 이해를 돕기 위해 아래 그림을 살펴보자.
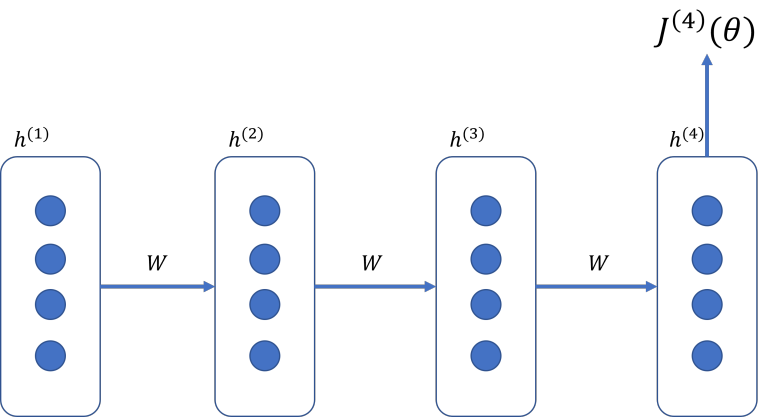
앞서 우리가 했던 ‘o’ 라는 철자를 예측하기 위해서 순차적으로 계산을 해서 최종적으로는 $J^{(4)}(θ)$ 에 대한 값을 구했다. 하지만, 값이 잘못 됬었고, 이를 위해 2개의 가중치를 수정한다고 말했다. 따라서 우리가 수정해야되는 값은 가장 처음에 설정한 가중치인 $h(1)$ 이 되며, 이를 계산하기 위한, $dJ^{(4)}/dh^{(1)}$ 을 계산해야 되며, 이는 다음과 같다.
$ \frac {\delta J^{(4)}} {\delta h^{(1)}} = \frac {\delta J^{(4)}} {\delta h^{(4)}} \times \frac {\delta h^{\left(4\right)}}{\delta h^{(3)}} \times \frac {\delta h^{(3)}} {\delta h^{(2)}} \times \frac {\delta h^{(2)}} {\delta h^{(1)}} $
위의 수식과 같이 계산을 하면, 역전파를 통해 계산된 그레디언트가 나오게 된다.
4) 한계점
여기서도 문제가 하나 있다. 만약 가중치 간의 그레디언트(dh(4)/dh(3), dh(3)/dh(2) , dh(2)/dh(1)) 가 1보다 작거나 1보다 큰 경우라면 어떨까? 결론부터 말하면, 그레디언트가 소실되거나 발산할 수 있다. 이런 현상이 발생한 원인은 하이퍼볼릭 탄젠트 함수로 역전파를 할 경우에 발생한다.
우선 위의 현상을 설명하기에 앞서, 우리가 계산한 수식을 일반화 시켜보자. 위의 수식에서 h(t) 에 대한 함수를 정리해보자면, 다음과 같다.
$ h^{(t)} = \tanh (w_h h^{(t-1)} + W_x x^{(t)} + b) $
위의 수식을 이용해 $dh(t)/d(t-1)$ 을 계산하자면, 다음과 같이 표현할 수 있다.
$ \frac {\delta h^{(t)}} {\delta h^{(t-1)}} = W_h \times \tanh (W_h h^{(t-1)} + W_x x^{(t)} + b) $
위의 식으로, 예제 문제를 간략하게 표현하자면 다음과 같다.
$ \frac {\delta J^{(4)}} {\delta h^{(1)}} = W_h^3 \times \tanh ^3 $
이를 일반화하기 위해서 특정 n번째 계층부터 시작해 m 번째 출력값까지 역전파를 진행한다고 가정하면, 다음과 같이 수식을 작성할 수 있다.
$ \frac {\delta J^{(m)}} {\delta h^{(n)}} = W_h^{(n-m)} \times \tanh ^{(n-m)} $
자, 그럼 다시 문제의 현상으로 되돌아와보자. 위의 일반화 수식에서 하이퍼볼릭 탄젠트를 미분한 값을 사용한 것을 확인할 수 있다. 이에 대해, 하이퍼볼릭 탄젠트 함수를 미분한 결과 그래프를 그려보자면, 아래 그림과 같다.
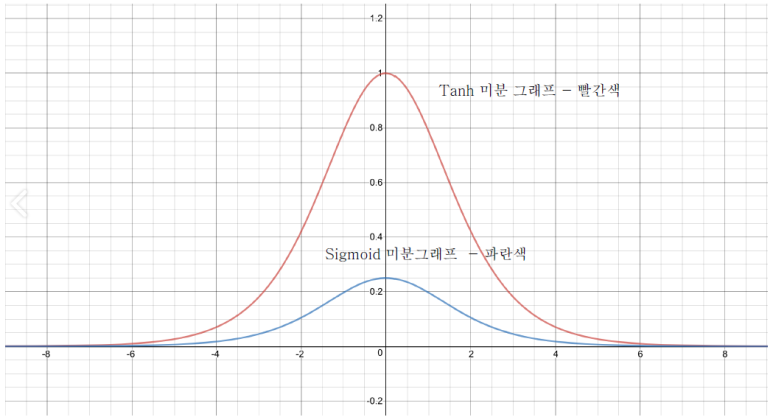
그림에서처럼 0일 때 1을 갖고, 그 외의 값에서는 0 ~ 1사이의 값을 갖는다. 따라서 위의 수식에서 가중치에 0에 가까운 값을 곱하게 되면, 가중치는 점점 작아지게되고, 여기에 덧붙여서, (n-m) 간의 차이가 큰 상황이라면, n 에 가까워 질 수록 그레디언트는 0에 근접하게 되며, 그레디언트 소실 문제를 발생시키고, 학습을 원활하게 할 수 없게 된다.
위의 예시에서는 하이퍼볼릭 탄젠트 함수를 사용해서 그레디언트 소실만 발생할 수 있지만, 만약 가중치의 값이 1보다 큰 경우라면, 반대로 그레디언트 폭주 현상이 발생할 수도 있다. 이러한 현상을 막기 위해 등장한 대표적인 모델로는 LSTM이 있으며, 다음 장에서 다룰 예정이다.
5. 실습: RNN 모델 생성하기
마지막으로 RNN 모델을 Tensorflow를 사용해서 구현해보는 실습을 해보도록 하자. 간단한 예제인만큼 먼저 샘플 데이터를 먼저 생성해보자.
[Python Code]
# 샘플데이터 생성하기
x = []
y = []
for i in range(6):
lst = list(range(i, i + 4))
x.append(list(map(lambda c: [c/10], lst)))
y.append((i + 4) / 10)
x, y = np.array(x), np.array(y)
for i in range(len(x)):
print(x[i], y[i])
[실행 결과]
[[0. ]
[0.1]
[0.2]
[0.3]] 0.4
[[0.1]
[0.2]
[0.3]
[0.4]] 0.5
[[0.2]
[0.3]
[0.4]
[0.5]] 0.6
[[0.3]
[0.4]
[0.5]
[0.6]] 0.7
[[0.4]
[0.5]
[0.6]
[0.7]] 0.8
[[0.5]
[0.6]
[0.7]
[0.8]] 0.9
다음으로 모델을 생성해보자. 모델은 간단하게 RNN 계층 1개와 최종 출력을 생성하기 위해 Dense 계층 1개로 구성한다.
[Python Code]
model = Sequential([
SimpleRNN(units=10, return_sequences=False, input_shape=[4, 1]),
Dense(1)
])
model.compile(optimizer="adam", loss="mse")
model.summary()
[실행 결과]
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
simple_rnn_1 (SimpleRNN) (None, 10) 120
dense (Dense) (None, 1) 11
=================================================================
Total params: 131
Trainable params: 131
Non-trainable params: 0
_________________________________________________________________
이제 모델을 학습하고, 학습된 모델로 예측까지 해보자.
[Python Code]
model.fit(x, y, epochs=100, verbose=0)
print(model.predict(x))
print(model.predict(np.array([[[0.6], [0.7], [0.8], [0.9]]])))
print(model.predict(np.array([[[-0.1], [0.0], [0.1], [0.2]]])))
[실행 결과]
[[0.38668048]
[0.5037124 ]
[0.6123263 ]
[0.7116213 ]
[0.8015863 ]
[0.882784 ]]
[[0.9560398]]
[[0.26315284]]
[참고자료]
https://wikidocs.net/21687
https://bubilife.tistory.com/36

댓글남기기