[Python Deep Learning] 12. Modern CNN Ⅳ : MobileNet

1. 개요

지금까지 살펴봤던 신경망들은 하나 같이 깊고, 연산을 처리하기 위해 사용되는 파라미터의 개수도 많은 편에 속한다. 때문에 학습을 하는 데에 시간도 오래걸리며, 빠르게 하기 위해서는 그만큼 많은 비용이 들어갔다.
하지만, 시간이 지나 현재에는 사물인터넷, 5G 등의 저전력 통신망에서도 딥러닝을 활용하려는 시도가 있었다. 이러한 환경에 맞춰서 등장하게 된 것이 바로 지금부터 다룰 MobileNet 이다.

2. MobileNet

1) 연산량 비교

앞서 개요에서 언급한 것처럼 MobileNet은 모바일 기기에서도 서비스가 가능한 가벼운 모델을 만들기 위해서 진행된 연구다. 때문에 핵심은 연산량과 파라미터 수를 줄이는 것이 목표이기 때문에 앞선 장인 Xception 에서 나온 Depthwise Separable Convolution 연산을 수행한다.

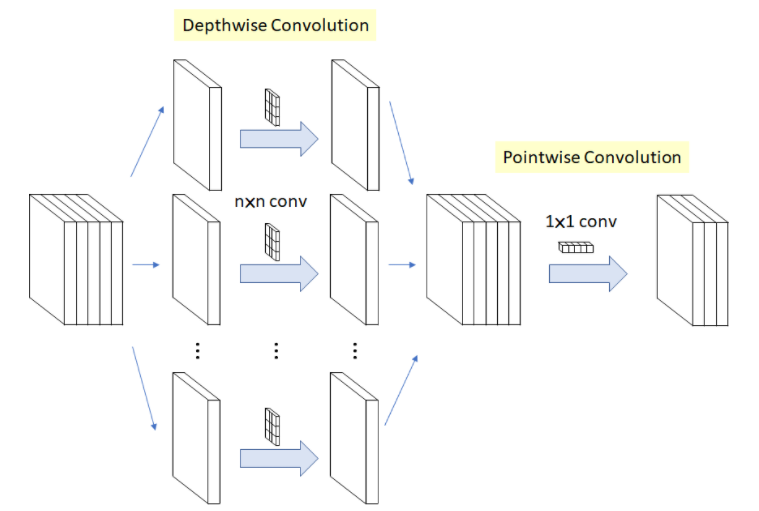
Xception 에서 소개를 했기 때문에 이번 장에서는 간략하게 집고 넘어가기로 하자. Depthwise Separable Convolution 은 위의 그림과 같이 2단계로 진행된다. 일반적인 Convolution 연산은 아래 그림과 같이 필터가 K x K 이고, 이 때 이미지의 높이와 너비가 F, 입력 채널 수가 N 이고, 출력 채널 수가 M 이라고 할 때, 총 연산량은 $ F^2 \times K^2 \times N \times M $ 만큼 작업하게 된다.

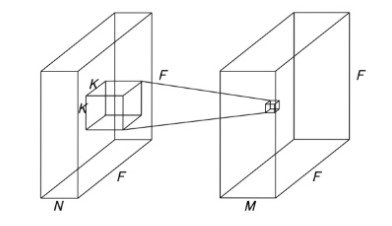
반면, Depthwise Separable Convolution 의 경우에는 Depthwise Convolution 과 Pointwise Convolution을 따로 수행해 합치는 방식이다. 따라서, 총 연산량은 아래 그림에서처럼 $ (F^2 \times K^2 \times N) + (F^2 \times 12 x N x M) $ 만큼 작업하게 된다.

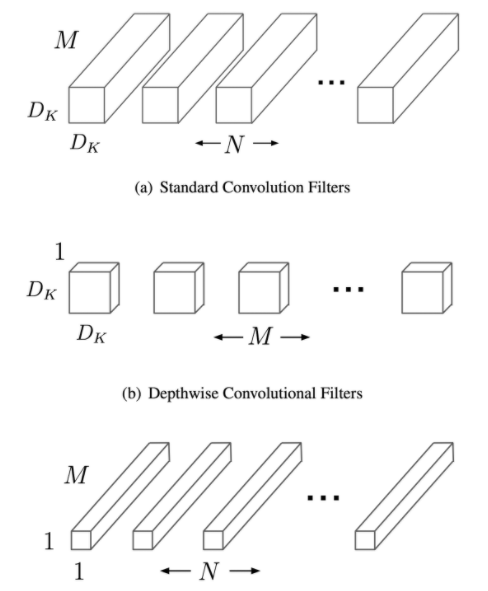
연산량의 비율은 $ K^2 \times M : K^2 + M $ 이며, 만약 위의 식에서, K = 2, M = 64 라고 잡을 경우, 연산량은 약 18배 정도 차이난다.

2) 구조적 비교

이번에는 구조적으로 어떤 차이가 있는 지 살펴보자. 구조적으로 가장 큰 차이는 당연하게도, Depthwise Separable Convolution 이다. 같은 연산을 사용하는 Xception 과의 차이는 Xception의 경우 shortcut 구조를 갖고 있고, 1x1 → 3x3 conv 연산을 사용하지만, MobileNet의 경우, Xception 과 반대로 3x3 → 1x1 순서로 conv. block 을 구성하고, 비선형성이 추가됬다는 점이 다르다. 다음으로 아래 그림을 통해 일반적인 convolution 블록과 Depthwise Separable Convolution 블록간의 구조적 차이를 살펴보자.

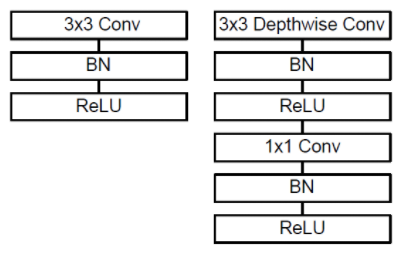
위의 그림에서 왼쪽은 일반적인 Convolution 연산 블록을 표현한 것이고, 오른쪽은 Depthwise Separable Convolution 연산 블록을 표현한 것이다. 차이점은 3x3 Depthwise Conv. 연산과 1x1 Conv. 연산 사이에 Batch Normalizeation 과 ReLU 연산이 추가되어 있는 것을 확인할 수 있다. 끝으로 전체 구조는 아래 표를 통해 확인할 수 있다.

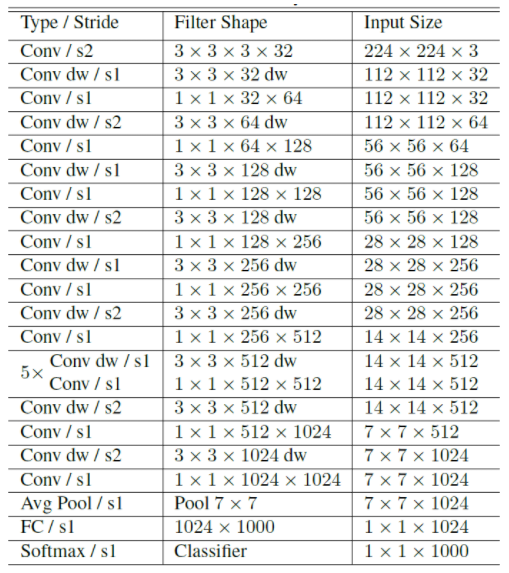
3. Width Multiplier & Resolution Multiplier

1) Width Multiplier

Width Multiplier는 input channel 과 output channel을 조절해주는 파라미터다. 전체적인 채널 수를 조절함으로써 더 가벼운 모델을 생성할 수 있다.

$D_K \cdot D_K \cdot \alpha M \cdot D_F \cdot D_F + \alpha M \cdot \alpha N \cdot D_F \cdot D_F $

$ \alpha $의 값은 1, 0.75, 0.5, 0.25를 가질 수 있으며, 기본값은 $ \alpha = 1 $ 로 설정된다. 따라서, 대략 위의 연산량 식에서 보았을 때 기존의 $ \alpha $ 가 없을 때의 수식과 $ {\alpha }^2 $ 만큼 차이가 나게 되는 것이다.

2) Resolution Multiplier

두 번째 파라미터는 Resolution Multiplier(ρ)이다. 이것은 input 이미지의 크기를 조절하는 역할을 한다. 일반적으로 input resolution이 224, 192, 160, 128을 갖도록 설정하게 된다.

$D_K \cdot D_K \cdot \alpha M \cdot \rho D_F \cdot \rho D_F + \alpha M \cdot \alpha N \cdot \rho D_F \cdot \rho D_F $

위와 같이 width와 같이 ρ2 만큼 연산량의 차이가 나게 된다.

3) 실험: 어떤 모델이 더 좋을까?

첫 번째 실험으로는 채널 수를 변경한 것과 모델 계층 수를 변경한 것을 비교한 것이다. 위에 있는 0.75 MobileNet 은 채널 수를 변화한 것이고, 아래에 있는 Shallow MobileNet 은 모델 내의 계층에 변화를 준 모델이다. 2개 모델에 대해서 ImageNet에서 제공한 데이터로 모델을 학습한 결과 정확도 측면에서보면, 모델의 계층 수를 늘리는 것보다, 채널의 크기를 더 깊게 만들어 주는 것이 좋다는 점을 확인할 수 있다.
두 번째 실험에서는 모델의 계층은 일정하게 유지하면서, 채널의 크기에 변화를 줬을 때, 어떤 현상이 나타나는지를 관찰한 것이다. 내용은 아래 표와 같다.

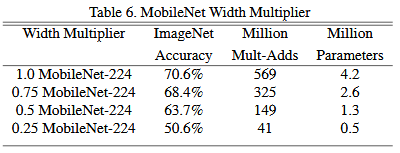
위의 표를 보면 모델의 계층 수는 224개로 일정하게 유지했지만, 입력 데이터의 채널 크기를 줄인 것으로 각각 100%, 75%, 50%, 25% 로 줄인 모델을 나타낸다. 우선 당연한 이야기지만, 채널 수가 줄어들면, 그만큼 학습에 사용되는 파라미터 수도 줄어들어 연산량 자체가 감소하지만, 그에 따라 정확도도 점점 감소하는 것을 볼 수 있다.
마지막으로, 이번에는 동일한 채널 크기에 대해서 계층 수에 변화를 줘봤다. 당연한 이야기이지만, 계층 수가 줄어들면 연산량이 감소하게 된다. 하지만, 그에 따라 정확도(Accuracy) 도 감소하는 것을 확인할 수 있다.

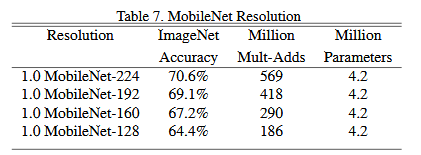
4. 구현하기

마지막으로 위에서 본 MobileNet 의 구조를 보면서 모델을 구현해보자. 현재는 V3 까지 나왔지만, 이번 예제에서 구현할 모델은 가장 초기 모델인 MobileNetV1을 구현할 것이다. 코드는 다음과 같다.

[Python Code]

import os
import numpy as np
import tensorflow as tf
from tensorflow.keras import Input
from tensorflow.keras.layers import Conv2D, DepthwiseConv2D, SeparableConv2D, BatchNormalization, Dense, AveragePooling2D, Activation
from tensorflow.keras import datasets as tfds
from tensorflow.keras.callbacks import ModelCheckpoint, EarlyStopping, ReduceLROnPlateau

def mobilnet_v1(x, alpha=1):
    def depthwise(x, _padding, _filter, _stride):
        x = DepthwiseConv2D(kernel_size=3, padding="same")(x)
        x = BatchNormalization()(x)
        x = Activation("relu")(x)
        x = Conv2D(filters=_filter, kernel_size=1, strides=_stride, padding="same")(x)
        x = BatchNormalization()(x)
        x = Activation("relu")(x)

        return x

    x = Conv2D(filters=int(32 * alpha), kernel_size=3, strides=2, padding="same")(x)
    x = BatchNormalization()(x)
    x = Activation("relu")(x)
    x = depthwise(x, "same", int(64 * alpha), 1)
    x = depthwise(x, "valid", int(128 * alpha), 2)
    x = depthwise(x, "same", int(128 * alpha), 1)
    x = depthwise(x, "same", int(256 * alpha), 2)
    x = depthwise(x, "same", int(256 * alpha), 1)
    x = depthwise(x, "valid", int(512 * alpha), 2)

    for i in range(5):
        x = depthwise(x, "same", int(512 * alpha), 1)

    x = depthwise(x, "valid", int(1024 * alpha), 2)
    x = depthwise(x, "same", int(1024 * alpha), 1)

    return x

[참고자료]
https://hichoe95.tistory.com/53