[Python Deep Learning] 10. Modern CNN Ⅱ : Squeeze - Excitation Network

1. 개요

일반적인 CNN 네트워크를 살펴보면, 컨볼루션 필터 하나씩 이미지 또는 피쳐맵의 수용영역(receptive field) 정보의 조합을 학습하게 된다. 이를 활성함수에 통과시키면 비선형적인 관계를 추론하고, 풀링과 같은 방법으로 크기가 큰 피쳐를 작게 만들어 한 번에 볼 수 있도록 만들기도 한다. 이런 방식으로 CNN은 global repceptive field 의 관계를 효율적으로 다루기 때문에 이미지 분류와 같은 영역에서 인간을 뛰어넘는 성능을 낼 수 있었다.
이러한 성능이 나올 수 있는 이유는 일반적인 CNN 구조보다 효율적으로 특징들을 잘 다룰 수 있는 다양한 구조에 대한 연구와 시도가 있었기 때문이며, 이번 장에서 다룰 SENet 역시 그러한 시도 중에 빛을 발한 결과이다.

2. Squeeze and Excitation Block

SENet의 궁극적인 목표는 Squeeze 와 Excitation 연산으로, 컨볼루션 연산을 통해 얻어진 피처맵에 대해 각 채널간의 상호의존성을 모델링함으로써, 모델의 표현력을 향상하는 것이다.
SENet의 경우에는 크게 2개의 과정으로 나눠볼 수 있다. 각 피쳐맵에 대한 전체정보를 요약해주는 Squeeze Operation 과 요약된 정보를 통해 각 피쳐맵의 중요도를 스케일해주는 Excitation Operation 이 있다. 그리고 이 두가지 과정을 하나의 연산으로 표현한 것이 아래 나와있는 SE 블록 (SE Block) 이다.

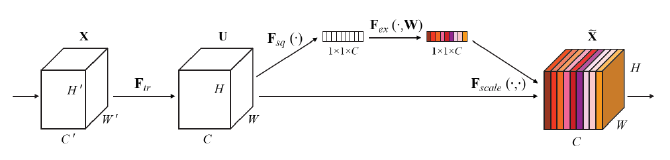
SE 블록이 갖는 장점으로는 다음과 같다.

[SE 블록의 장점]

1. 신경망 어느 위치에서든 상관없이 바로 사용이 가능하다.
2. 파라미터 증가량에 비해 모델 성능 향상도가 매우 크기 때문에, 모델 복잡도, 계산 복잡도가 크게 증가하지 않는다.

그렇다면 어떤 구조이기에 위와 같은 장점이 있는지 세부적으로 살펴보도록 하자.

1) Squeeze : Global Information Embedding

먼저 Squeeze 연산부터 알아보자. 단어 뜻 그대로 짜내는 연산인데, 이를 다르게 말하자면, 각 책널의 중요 정보만 추출해서 가져가겠다는 의미이다. 따라서 부분 수용영역 (local receptive field) 이 매우 적은 네트워크 하위 부분이라면, 이러한 정보 추출의 개념이 매우 중요하다. 논문상에서는 GAP (Global Averages Pooling)을 사용했다. GAP 을 사용하는 경우, global spatial information을 channel descriptor 로 압축하는 것이 가능하다. 수식으로 나타내면 다음과 같다.

$ z_c = F_{sq}(u_c) = \frac {1} {H \times W} \sum _{i=1}^H \sum _{j=1}^W u_c(i, j) $

위의 수식에서 Fsq 는 컨볼루션 연산을 의미하고 HxW 는 2차원의 특성맵을 의미한다. 이러한 특성 맵은 C 개 만큼 존재하며, 결과적으로, H x W x C 크기의 특성맵인 U 가 생성된다고 볼 수 있다. 이 후 C 개의 채널을 2차원 특성맵들을 1 x 1 사이즈의 특성맵으로 변환해주는 작업을 수행한다. 결국 Squeeze 연산은 간단하게 말해서 GAP을 통해 각 2차원 특성맵을 평균내서 하나의 값을 얻는 과정이라고 할 수 있다.

2) Excitation : Adaptive Recalibration

앞서 Squeeze 연산을 통해 이미지를 압축했다면, 이를 재조정해주는 작업이 필요하다. 이러한 연산을 Excitation 연산이라고 하며, 채널 간 의존성을 계산하게 된다. 하지만 연산을 하기 위해서는 아래의 2개 전제 조건이 필요하다.

[전제 조건]

1. 채널들 간의 비선형적인 관계를 학습할 수 있어야 한다.
2. 다양한 채널을 동시에 강조할 수 있어야 한다.

논문에서는 Fully Connected Layer 와 비선형 함수를 사용하여, 간단하게 아래 그림과 같이 구현하였다.

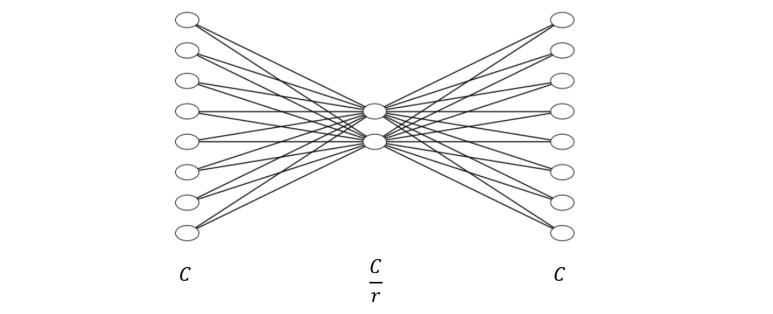
주목할 점은 r 에 해당하는 reduction ratio 를 통해 노드 수를 줄인 다는 점이다. 결과적으로 2개의 Fully-Connected 레이어를 더해서 각 채널의 상대적 중요도를 알아내는 연산이라고 할 수 있다. 그리고 이에 대한 결과는 스케일링 처리가 되어 모두 0 ~ 1 사이의 값을 가지게되며, 채널들의 중요도에 따라 스케일 된다. 위의 SE Block 을 구현해보자면, 아래와 같이 표현할 수 있다.

[Python Code]

import tensorflow as tf
from tensorflow import keras as K

def squeeze_excitation_block(input, ratio=16):
init = input

    if K.backend.image_data_format() == "channels_first":
        channel_axis = 1
    else:
        channel_axis = -1

    filters = init._keras_shape[channel_axis]
    se_shape = (1, 1, filters)

    block = K.layers.GlobalAveragePooling2D()(init)
    block = K.layers.Reshape(se_shape)(block)
    block = K.layers.Dense(filters // ratio, activation='relu', kernel_initializer='he_normal', use_bias=False)(block)
    block = K.layers.Dense(filters, activation="sigmoid", kernel_initializer="he_normal", use_bias=False)(block)

    if K.backend.image_data_format() == "channels_first":
        block = K.layers.Permute((3, 1, 2))(block)

    result = K.layers.multiply([init, block])

    return result

다음으로 실제 적용된 예시를 살펴보도록하자. 아래 그림은 SE 블록을 Inception이나 ResNet 처럼 skip connection이 있는 경우에는 skip connection 부분에 추가했다.

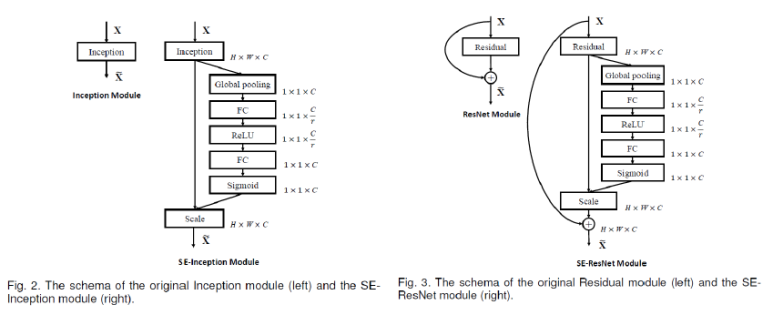
3. 모델 구조 및 복잡도 퍼포먼스

앞서 본 것처럼 SE 블록을 추가한 네트워크의 구조를 보면 알 수 있듯이, 모델에 대한 성능은 올라가지만, 그만큼 모델이 무겁고 복잡해지기 때문에 당연하게도 trade-off 가 발생하게 된다. 논문에서는 SE 블록을 ResNet-50 인 모델에 적용한 SE-ResNet-50 네트워크를 이용해서 계산 복잡도를 측정했다. 논문의 내용에 따른면, 측정한 결과, 모델에 대한 복잡도는 0.26% 만큼 증가했지만, 모델에 대한 오류는 상당히 많이 낮아지는 것을 확인할 수 있었다. 그만큼 squeeze, excitation, channel-wise scaling 연산 모두 계산 복잡도가 그리 높지 않다는 것을 의미한다.
SE 블록에서 계산복잡도에 영향을 주는 변수는 reduction ratio (r) 인데, 이를 적용했을 때의 추가되는 파라미터수는 아래 수식의 계산 결과와 동일하다.

$ N_{param} = \frac {2} {r} \sum _{s=1}^S N_s \cdot C_s^2 $
$ (S: 스테이지 수, C: 출력채널의 차원, N: 스테이지 S에서 반복되는 블록 수) $

앞선 측정 결과는 위의 수식에서 r 값을 변경해가면서 실험을 했고, 아래 표의 내용처럼 r=16 일 때가 에러가 크게 줄어들거나 늘지 않는 최적의 성능임을 보여 주었다.

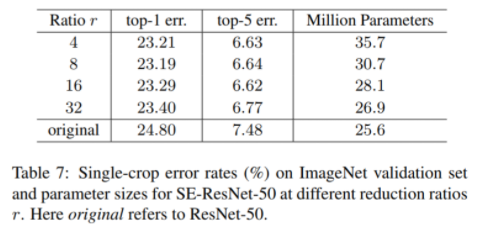
추가적으로 250만개의 파라미터만 추가로 들어가는데, 그래도 10% 정도만 증가한다고 하며, 마지막 레이어의 SE 블록은 제거해도 성능 상 큰 차이를 보이지 않았다고 한다.

[참고자료]
https://jayhey.github.io/deep%20learning/2018/07/18/SENet/ https://bskyvision.com/640 https://smcho.tistory.com/22