[Python Deep Learning] 1. Tensorflow

1. Tensorflow

구글에서 만들었으며, 딥러닝을 쉽게 구현할 수 있도록 다양한 기능을 제공하는 라이브러리이다.

텐서플로 자체는 기본적으로 C++ 과 파이썬을 기반으로 구현되어있으며, 아래 그림과 같이 Python, Java, Go 와 같이 여러가지 언어를 지원한다. 최근에는 Tensorflow.js 와 같이 자바스크립트로도 구현할 수 있도록 지원한다. 뿐만 아니라 시각화를 도와주는 텐서보드를 제공하여, 딥러닝 학습 과정을 추적하는 데 유용하게 사용된다.

2. Tensor

텐서(Tensor)란, 딥러닝에서 데이터를 표현하는 방식이다. 정확하게는 행렬과 같은 2차원형태의 배열을 높은 차원(층)으로 구성된 다차원 배열이다. 예를 들어 이미지의 경우에는 흑백인 경우에는 2차원배열 1개로 구성할 수 있지만, 흔히 우리가 말하는 컬러(RGB) 의 경우 Red, Green, Blue 에 해당하는 각각의 2차원 배열을 3개의 층으로 쌓아서 만드는 다차원배열로 표현할 수 있다.

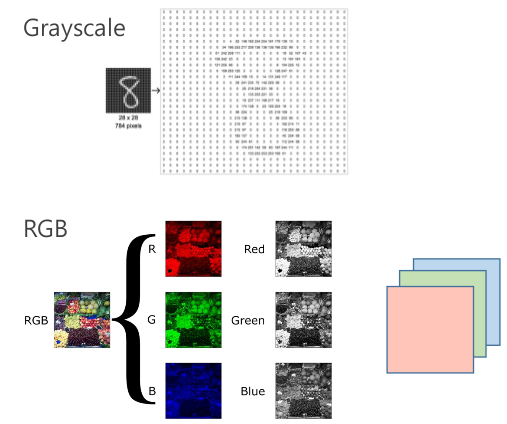
구체적인 내용은 뒤에서 좀 더 자세히 다룰 예정이다.

3. Tensorflow 설치하기

텐서플로는 앞서 언급한 데로 C++ 과 파이썬을 기반으로하는 만큼 2개 언어로 설치가 가능하다. 이번 절에서는 파이썬을 사용해서 텐서플로를 설치해보자.

1) CPU vs. GPU

텐서플로는 설치하려는 PC에 GPU가 있는지 없는지에 따라 적용할 수 있는 버전이 달라진다. CPU나 GPU 버전 중 1개만 설치하는 것이 좋으며, 기본적으로는 CPU를 사용한다. 설치하기 위한 커맨드는 다음과 같다.

[CMD]

pip install tensorflow==2.x   # 여기서의 x 는 버전 숫자를 의미한다.

만약 설치하려는 PC에 GPU 모듈이 존재한다면, 아래와 같이 GPU를 사용하는 텐서플로 GPU 버전을 다운 받아 사용할 수 있다. 물론 설치하기 전에 CUDA를 먼저 설치하길 권장한다. 설치는 아래에 나온 Pytorch 설치 과정에서 언급했기때문에 해당 내용을 참고하기 바란다.

[Pytorch] 1. 개요 및 설치

GPU 버전에 대한 설치 커맨드는 다음과 같다.

[CMD]

pip install tensorflow-gpu==2.x  # 여기서의 x 는 버전 숫자를 의미한다.

설치가 완료됬다면, 아래와 같이 텐서플로를 import 하고 버전확인까지 수행한다.

[Python Code]

import tensorflow as tf

print(tf.__version__)

[실행 결과]

2020-10-20 22:17:15.919724: I tensorflow/stream_executor/platform/default/dso_loader.cc:48] Successfully opened dynamic library cudart64_101.dll

2.3.0

2) Google Colab

파이썬 프로그램을 브라우저 환경에서 직접 실행할 수 있도록 구글에서 제공하는 노트북 파일로, 텐서플로도 지원하기 때문에, 부득이하게 설치가 불가한 경우에 인터넷만 연결되어있다면 사용이 가능하다.

더 자세한 내용은 텐서플로 공식문서를 참고하기 바란다.

[텐서플로 2.0 시작하기: 초보자용

TensorFlow Core](https://www.tensorflow.org/tutorials/quickstart/beginner?hl=ko)

4. 텐서플로 기초

1) 난수 생성

난수는 신경망에서 꼭 필요한 작업으로, 특히 신경망을 처음 사용할 때, 초기값을 지정해줘야하며, 이를 랜덤한 숫자들로 사용해야하기 때문이다. 가장 많이 사용되는 방법은 Xavier 초기화 방법과 He 초기화 방법을 많이 사용한다. 위의 2가지 방법은 랜덤하지만, 어느 정도의 규칙성이 있는 범위 내에서 난수를 생성해준다. 사용방법은 아래와 같다.

[Python Code]

rand_num = tf.random.uniform([1], 0, 1)
print(rand_num)

[실행 결과]

tf.Tensor([0.17084599], shape=(1,), dtype=float32)

위의 코드에서 사용한 tf.random.uniform() 함수는 균일분포의 난수를 생성한다. 균일분포란, 최소값과 최대값 사이의 모든 수가 나올 확률이 동일한 분포에서 수를 뽑는 것을 의미한다. 다음으로 함수 내에 선언한 파라미터 값의 의미를 살펴보자. 첫번째로 [1] 는 출력 결과의 shape 을 의미하며, 위의 예시는 1차원으로 선언했다. 두 번째로 나오는 0은 최소값을, 세 번째에 나오는 1은 최대값을 의미한다.
위의 설명 중 shape 은 행렬을 구성하는 행, 열 과 같이 차원의 수를 나타내는 값이다. 차원을 확인하려면 아래와 같이 생성된 텐서 객체에 .shape 값을 확인하면 된다.

[Python Code]

print(rand_num.shape)

[실행 결과]

(1,)

위의 예시에서는 1차원의 텐서를 생성하도록 설정했기 때문에 shape 역시 (1,) 로 1차원 텐서임을 표현했다. 만약 위의 예시와 달리, 직접 텐서의 shape을 확인하려는 경우에는 제일 외곽에 위치한 대괄호에 해당하는 요소의 갯수를 세며, 외부에서 내부로 이동하면서 계산하면 된다.

[예시-차원 수 계산하기]
ex. 
[[1, 2],
[3, 4]]

[1, 2] , [3, 4] 이므로 2행, [1], [2] 이므로 2열이 된다. 따라서 위의 예시에 나온 텐서의 shape 은 (2, 2) 인 텐서가 된다. 이번에는 shape에 들어가는 숫자 및 차원을 변경해서, 난수를 shape의 개수 만큼 생성해보자.

[Python Code]

rand_num = tf.random.uniform([2,2], 0, 1)
print(rand_num)

[실행 결과]
tf.Tensor(
[[0.37026608 0.35084248]
[0.30862093 0.49645138]], shape=(2, 2), dtype=float32)

위의 예제는 2x2 인 난수 행렬을 생성하였다. 이처럼 첫번째 인수에 콤마( , ) 를 구분자로 하여 각 차원별로 원하는 개수를 입력으로 넣을 수 있다.

지금까지는 균일분포로 난수를 생성하였다면, 이제부터는 정규분포를 사용해서 난수를 생성해보자. 정규분포란, 가우시안 분포라고도 불리며, 그 중 평균은 0, 표준편차는 1인 분포를 표준정규분포라고 한다. 분포를 그래프로 표현하면 가운데가 높고 양극단으로 갈수록 낮아져 0을 기점으로 종모양의 분포를 나타낸다.
정규분포를 이용한 난수를 생성하려면 tf.random.normal() 함수를 사용하면된다. 함수에 사용되는 인자는 tf.random.uniform() 함수와 유사하다. 첫 번째 인수로는 shape 을 입력하면 된다. 하지만, 2번째와 3번째인자는 최소값, 최대값이 아닌, 평균과 표준편차를 입력으로 넣어줘야한다.

[Python Code]

rand_num = tf.random.normal([2], 0, 1)
print(rand_num)

[실행 결과]

tf.Tensor([-1.2944226  -0.96046746], shape=(2,), dtype=float32)

2) 뉴런 생성하기

뉴런이란 신경망에서 가장 기본적인 구성 요소이며, 입력을 받아 계산 후 출력하는 단순한 구조이다.

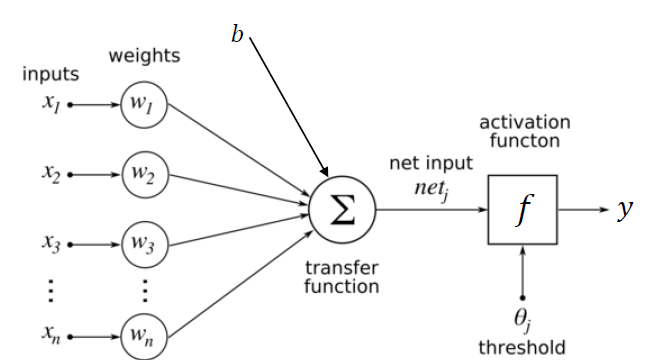
(1) 입력계층

입력을 받아 다음 계층으로 전달하는 역할을 수행하며, 특징 추출에 대한 문제가 존재한다. 계층의 크기는 노드의 개수이며, 이는 입력되는 스칼라 값의 개수라고 할 수 있다. 하지만, 실제로는 벡터의 형식으로 입력이 들어오기 때문에 입력 벡터의 크기라고 보는 것이 맞다.

(2) 은닉계층

입력 계층과 연결된 결합계층이며, 입출력의 관점에서는 보이지 않는다. 은닉계층의 수에 따라 앝은 신경망과 깊은 신경망으로 나뉘는데, 얕은 신경망의 경우에는 은닉층을 1개만 사용하고, 2개이상의 은닉층을 사용하게 되면, 깊은 신경망으로 볼 수 있다.
은닉계층의 또다른 특징은 입력계층에 존재하는 모든 노드와 연결되어있다는 점이다. 정확히는 입력 값에 가중치를 곱한 결과를 은닉계층의 결과로 사용하기 때문이다.

(3) 활성화 함수

활성화 함수는 뉴런의 출력값을 정하는 함수이고, 은닉계층에서 계산된 결과물을 입력으로 한다. 사용되는 함수는 주로 시그모이드 계열이나, ReLU 등을 사용하게 된다.

(4) 출력계층

활성화 함수의 결과를 출력해주는, 최종적인 결과를 출력하는 계층이라고 할 수 있다. 활성화 함수가 적용된 결과를 출력으로 사용하기 때문에, 신경망의 기능은 출력 계층의 활성화 함수에 의해 결정된다고도 볼 수 있으며, 출력 스칼라 값의 개수 만큼 출력 계층의 크기가 결정된다.

위의 내용을 코드로 구현해보자.

[Python Code]

import numpy as np
import pandas as pd
import math

import tensorflow as tf

def sigmoid(x):
    return 1 / (1 + math.exp(-x))

x = 1
y = 0
w = tf.random.normal([1], 0, 1)

output = sigmoid(x * w)
print(output)

[실행 결과]

0.19278175479691903

위의 코드에서는 입력을 x = 1, w 는 정규분포를 따르는 난수 1개를 생성하였고, 이에 대한 뉴런의 출력은 x * w 에 sigmoid 함수를 적용시켜서 생성된 결과이다. 이 때, 만약 실제 y 값(정확히는 기대 출력)이 코드에서처럼 0이라고 가정한다면, 뉴런에서 나온 결과와는 0.19 정도의 차이가 존재한다.
실제 결과와 예측 결과 간의 차이를 오차(Error) 라고 하며, 뉴런은 오차가 0에 가까워지도록 학습해서 출력이 기대 출력에 가까운 값을 얻게 된다. 이는 곧 가중치인 w를 수정하여 학습을 수행한다고 할 수 있다.

가중치 w 를 학습하기 위해서는 경사하강법(Gradient Descent) 이라는 기법을 이용한다. 자세한 내용은 추후에 다루기로 하자. 어쨌든 경사하강법이라는 것을 사용해서 w 의 값을 변화시키게 되는데, w 라는 값은 입력과 학습률, 에러를 곱한 값을 모두 더해주는 것이다. 가중치를 업데이트 하는 방법을 수식으로 표현하면 다음과 같다.

$ w = w + x \times \alpha \times error $

여기서 중요한 것은 학습률(α) 인데, 가중치를 업데이트하는 속도라고 이해하면 된다. 때문에 학습률을 너무 크게 잡으면 학습이 빠르게 진행되지만, 과하게 학습을 수행함으로써 적정 수치를 벗어날 수 있고, 반대로 너무 작으면 학습을 정밀하게 수행하지만, 그만큼 시간이 오래 소요된다는 트레이드 오프(Trade-Off)가 발생한다. 아래 예제에서는 학습률을 0.1로 설정하였다.

[Python Code]

for i in range(1000):
    output = sigmoid(x * w)
    err = y - output
    w = w + x * 0.1 * err

    if i % 100 == 99:
        print(i+1, err, output)

[실행 결과]

100 -0.009432804909735767 0.009432804909735767
200 -0.00862609876891491 0.00862609876891491
300 -0.00794605281218332 0.00794605281218332
400 -0.007365072591480231 0.007365072591480231
500 -0.006863046458448873 0.006863046458448873
600 -0.006424887496195802 0.006424887496195802
700 -0.006039175660590694 0.006039175660590694
800 -0.005697040778043125 0.005697040778043125
900 -0.00539150549408177 0.00539150549408177
1000 -0.005117000447653804 0.005117000447653804

위의 코드에서처럼 가장 먼저 출력 결과를 생성하고, 실제 결과와 출력결과 간의 오차를 계산한다. 마지막으로 오차를 이용해 경사하강법에 따른 가중치 수정값을 계산하고, 수정 값을 변경 전 가중치에 더하는 방식으로 가중치를 업데이트 한다.
하지만 위와 같은 구조인 경우, 문제가 발생할 수 있다. 예를 들어 입력값이 0일 때 출력이 1을 얻는 뉴런을 생성한다고 가정해보자. 그럴 경우 오차가 변하지 않기 때문에, 출력 역시 변동이 없다. 아래의 예시를 통해 확인해보자.

[Python Code]

x = 0
y = 1
w = tf.random.normal([1], 0, 1)

for i in range(1000):
    output = sigmoid(x * w)
    error = y - output
    w = w + x * 0.1 * error

    if i % 100 == 99:
        print(i+1, error, output)

[실행 결과]

100 0.5 0.5
200 0.5 0.5
300 0.5 0.5
400 0.5 0.5
500 0.5 0.5
600 0.5 0.5
700 0.5 0.5
800 0.5 0.5
900 0.5 0.5
1000 0.5 0.5

위와 같은 현상을 방지하기 위해 편향(bias) 라는 값을 추가해줘야 한다. 단어의 뜻 그대로, 입력에 대해 한쪽으로 치우친 고정 값을 받아 입력이 0이라고 해도 뉴런이 학습하지 못하는 현상을 해결하는 역할이다.

[Python Code]

x = 0
y = 1
w = tf.random.normal([1], 0, 1)
b = tf.random.normal([1], 0, 1)

for i in range(1000):
    output = sigmoid(x * w + 1 * b)
    error = y - output
    w = w + x * 0.1 * error
    b = b + 1 * 0.1 * error

    if i % 100 == 99:
        print(i+1, error, output)

[실행 결과]

100 0.09727899885951885 0.9027210011404811
200 0.05097905538856862 0.9490209446114314
300 0.03422328581376666 0.9657767141862333
400 0.025681663808638233 0.9743183361913618
500 0.020525425060062497 0.9794745749399375
600 0.01708173069755614 0.9829182693024439
700 0.014621632230769621 0.9853783677692304
800 0.012777640607069762 0.9872223593929302
900 0.011344619351907115 0.9886553806480929
1000 0.010199373963886482 0.9898006260361135

코드에서처럼 편향 역시 가중치와 동일하게 난수로 초기화하며, 뉴런에 더해져 출력을 계산하게 된다.

5. Tensorflow 1.x vs Tensorflow 2.x

앞으로 우리가 배울 버전은 Tensorflow 2.x 버전이 될 것이다. 때문에 기존에 사용하던 1.x 버전에 비해서 어떤 점이 바뀌었는지에 대해서는 알고 넘어갈 필요가 있으며, 좀 더 편리하고 효율적으로 코드를 작성하기 위해서 어떻게 사용하는지를 하나씩 살펴보도록 하자.

1) Keras

케라스(Keras) 는 딥러닝 모델을 만들고 훈련하기 위해, 신경망의 기초 구성 요소가 포함된 API이다. 텐서플로를 포함해, CNTK, MxNET, Theano 등 여러 딥러닝 엔진에 통합될 수 있다.
특히 텐서플로의 버전이 2.0이 되면서 가장 큰 변화가 케라스가 텐서플로 라이브러리의 일부가 되었다는 점이다. 사용 방법은 tf.keras 로, 텐서 플로 내부에 구현된 케라스를 사용할 수 있다.

2) Tensorflow 1.x 계산그래프 구조

Tensorflow 1.x 에서는 실행까지 총 2단계에 걸쳐서 수행되었다. 먼저 만들고자 하는 신경망의 구조를 먼저 생성하며, 이를 계산그래프의 정의라고도 부른다. 이 후, 정의된 신경망을 학습시키는 그래프 실행 단계를 통해 학습이 진행된다.

(1) 계산 그래프 정의

여기서 말하는 계산 그래프란 노드와 엣지를 가진 네트워크의 구조를 의미한다. 여기서는 텐서 객체와 수행할 모든 연산 객체가 정의되며, 각 노드는 0개 이상의 입력을 가질 수 있지만, 반드시 하나의 출력만 가져야한다. 또한 네트워크에서 노드는 텐서나 연산을 나타내고, 엣지는 연산 간에 흐르는 텐서를 나타낸다.

(2) 그래프 실행

그래프의 실행은 텐서와 연산 객체가 평가 환경을 캡슐화한 “세션(Session)” 이라는 객체를 사용해 수행하게 된다. 세션 객체는 하나의 계층에서 다른 계층으로 정보의 실제 계산 및 전송이 워지는 곳이다. 때문에 다른 텐서 객체의 값은 세션 객체에서만 초기화, 접근, 저장이 가능하다.

(3) 그래프 구조를 사용한 이유

그렇다면 왜 텐서플로 1.x 버전에서는 그래프를 사용했을까? 첫 번째 이유로는 신경망을 설명해 주기에 가장 자연스러운 비유가 가능하기 때문이다. 앞서 신경망의 구조에 대해서 설명할 때, 예시 사진을 보면 알 수 있듯이. 노드와 화살표로 구성된 그래프 구조를 갖고 있다는 것을 알 수 있다.
두 번째는 그래프는 공통 하위 표현식을 제거하고, 커널을 합치며, 중복 표현을 제거해주는 특징이 있ㅇ어 자동으로 최적화가 가능하다는 점이다.
세 번째는 훈련을 하는 도중에도 쉽게 배포하는 것이 가능하며, 환경도 기존의 서버와 같은 다양한 환경에 배포할 수 있다는 장점이 있다.

(4) 변수, 상수, 플레이스홀더 사용법

텐서플로는 다양한 수학 연산을 텐서로 정의해서 수행하는 라이브러리를 제공한다. 여기서 텐서는 기본적으로 n차원의 배열이며, 모든 유형의 데이터(스칼라, 벡터, 행렬 등)는 특수한 형태의 텐서라고 정의한다.
텐서플로에서는 3가지 유형의 텐서가 있다. 첫 번째 상수는 값을 변경할 수 없는 텐서이며, 계산 그래프 정의에 저장되기 때문에 그래프가 로드될 때 같이 로드 되고, 메모리의 사용이 크다.
두 번째로 변수는 세션 내에서 값을 갱신할 때 주로 사용되며, 상수와는 달리 별도로 저장되며, 매개변수 서버에는 존재하지 않는다.
마지막으로 플레이스홀더는 텐서플로 그래프에 값을 대입할 시에 사용되는 텐서이다. 일반적으로 feed_dict() 와 함께 데이터를 공급할 때 사용되고, 훈련 중에 새로운 훈련예시를 제공할 때 사용된다.
위의 3가지에 대한 사용법은 다음과 같다.

[Python Code - Tensorflow 1.x]

t1 = tf.constant(4)  # 상수 사용법
t2 = tf.Variable([0, 1, 2])  # 변수 사용법

initial_op = tf.global_variables_initializer()  # 변수 초기화

saver = tf.train.saver()  # 변수 저장

tf.placeholder(dtype, shape=None, name=None)  # Placeholder 사용법

(5) 세션 생성, 실행, 종료

세션그래프를 생성하고 실행하려면 아래 코드와 같이 작성하면 된다.

[Python Code - Tensorflow 1.x]

x = tf.placeholder("float")
y = 2 * x
data = tf.random_uniform([4, 5], 10)
with tf.Session() as session:
x_data = session.run(data)
print(session.run(y, feed_dict = {x:x_data}))

3) Tensorflow 2.x 수정 사항

(1) 즉시 실행

텐서플로 1.x 의 경우 정적 그래프를 보여줬다면, 2.x 에서는 세션 인터페이스나 플레이스홀더 없이도 즉각적으로 실행시킬 수 있다. 이는 곧, 더 이상 정적 그래프를 생성할 필요가 없다는 의미이며, 동시에 모델의 정의를 동적으로 정의 및 실행이 가능하다는 의미이다.

(2) 오토그래프

텐서플로 2.x 에서는 기본적으로 if-while, print() 및 기타 파이썬 기본 특징과 같은 제어 흐름을 포함하는 명령형 파이썬 코드를 지원하고, 순수하게 텐서플로 그래프 코드로 변환할 수 있다는 점이다. 이 때 사용되는 것이 바로 오토그래프이다. 오토그래프는 즉시 실행 파이썬 코드를 가져와서 자동으로 그래프 생성 코드로 변환해준다. 사용방법은 파이썬 코드에 특정 데코레이터인 tf.function을 어노테이션 처럼 작성하면 된다.

[Python Code - Tensorflow2.x 오토그래프 지원기능]

import tensorflow as tf

def linear_layer(x):
    return 2 * x + 3

@tf.function
def simple_nn(x):
    return tf.nn.relu(linear_layer(x))

def simple_function(x):
    return 3 * x

tf.function을 사용할 경우, 하나의 주 함수에만 어노테이션을 달면 해당 함수에서 호출된 다른 모든 함수에도 자동으로 최적화된 계산 그래프로 전환된다는 점이 특징이다.
만약 자동으로 생성된 코드를 볼 필요는 없지만, 궁금한 경우 아래의 코드를 사용해서 살펴볼 수 있다.

[Python Code]

print(tf.autograph.to_code(simple_nn.python_function, experimental_optional_features=None))

(3) Keras API

앞서 언급한 것처럼 가장 큰 변화는 케라스가 텐서플로에 포함되었다는 점이다. 사실 텐서플로 1.x 는 로우레벨의 API를 제공한다. 이러한 이유로 연산 그래프를 작성한 후에 컴파일을 하고, 실행해서 모델을 작성했다.
하지만, 케라스에서는 순차적 API, 함수적 API, 모델 서브클래싱이라는 3가지 프로그래밍 모델과 함께 고수준의 API를 제공한다.

① 순차적 API
순차적 API 는 매우 직관적이고 간결한 모델이다. 예시는 아래와 같다.

[Python Code]

model = tf.keras.Sequential([
    tf.keras.layers.Dense(units=48, activation='relu', input_shape=(12,)),
    tf.keras.layers.Dense(units=24, activation='relu'),
    tf.keras.layers.Dense(units=12, activation='relu'),
    tf.keras.layers.Dense(units=2, activation='softmax')
])

② 함수적 API
함수적 API 는 다중 입력, 다중 출력, 비순차 흐름과의 잔존 연결, 공유, 재사용 가능 계층을 포함해 좀 더 복잡한 모델을 구현할 때 사용하는 방법이다.
예시는 아래와 같다.

[Python Code]

import tensorflow as tf

def build_model():
    # 가변길이 시퀀스
    text_input_a = tf.keras.Input(shape=(None,), dtype='int32')

    # 가변길이 정수 시퀀스
    text_input_b = tf.keras.Input(shape=(None,), dtype='int32')

    # 1000개의 고유 단어를 128차원 벡터에 매핑 후 임베딩
    shared_embedding = tf.keras.layers.Embedding(1000, 128)

    # 양쪽입력을 인코딩하고자 동일한 계층 재사용
    encoded_input_a = shared_embedding(text_input_a)
    encoded_input_b = shared_embedding(text_input_b)

    # 최종적으로 2개의 로지스틱 예측
    prediction_a = tf.keras.layers.Dense(1, activation='sigmoid', name='prediction_a')(encoded_input_a)
    prediction_b = tf.keras.layers.Dense(1, activation='sigmoid', name='prediction_b')(encoded_input_b)

    # 공유 모델
    model = tf.keras.Model(
        inputs=[text_input_a, text_input_b]
        , outputs=[prediction_a, prediction_b]
    )

    tf.keras.utils.plot_model(model, to_file="shared_model.png")

build_model()

③ 모델 서브클래싱
케라스에서 제공하는 3가지 방법 중 최고의 유연성을 제공하면 일반적으로 자신의 계층을 정의해야할 때 사용하는 방법이다. 복잡도 측면에서 더 높은 비용이 들기 때문에 실제 필요할 때만 사용하는 것이 좋다. 만약 사용자 정의 계층을 생성하려면 tf.keras.layers.layer() 를 서브 클래싱 하고 아래에 정의한 메소드들을 포함시켜주면 된다.

• init : 선택적으로 이 계층에서 사용할 모든 하위 계층을 정의하는 데 사용한다.
• build: 계층의 가중치를 생성할 대 사용한다. 추가적으로 dd_weight() 로 가중치를 추가할 수 있다.
• Call: 순방향 전달을 정의한다. 계층이 호출되고 함수 형식으로 체인되는 부분이다.

위의 내용말고, 선택적으로 get_config() 를 사용해 계층을 직렬화 할 수 있고, from_config() 를 사용하면 역직렬화를 할 수 있다.

[Python Code]

class MyLayer(layers.Layer):

    def __init__(self, output_dim, **kwargs):
        self.output_dim = output_dim
        super(MyLayer, self).__init__(**kwargs)

    def build(self, input_shape):
        self.kernel = self.add_weight(
            name='kernel',
            shape=(input_shape[1], self.output_dim),
            initializer='uniform'
            trainable=True
        )

    def call(self, inputs):
        return tf.matmul(inputs, self.kernel)

(4) Callback

훈련 중에 동작을 확장하거나 수정하고자 모델로 전달하는 객체다. 이번에 텐서플로에 포함된 케라스에서는 사용하기 좋은 몇 가지 콜백들이 있다.

① tf.keras.callbacks.ModelCheckpoint
정기적으로 모델의 체크포인트를 저장하고 문제가 발생할 때 복구하는 용도로 사용한다.

② tf.keras.callbacks.LearningRateScheduler
최적화하는 동안 학습률을 동적으로 변경할 때 사용한다.

③ tf.keras.callbacks.EarlyStopping
검증 성능이 한동안 개선되지 않을 경우 훈련을 중단하기 위해 사용한다.

④ tf.keras.callbacks.TensorBoard
텐서보드를 사용해 모델의 행동을 모니터링할 때 사용한다.

(5) 모델 및 가중치 저장

모델을 훈련한 후 가중치를 지속적으로 저장해두면 유용할 때가 있다. 이번 텐서플로 2.x 버전에서는 가중치의 경우에는 아래와 같이 저장할 수 있다.

[Python Code]

model.save_weights('./weights/my_model')

저장한 가중치를 다시 호출할 때는 반대로 load_weights() 메소드를 사용한다.

[Python Code]

model.load_weights(file_path)

모델을 저장할 때는 JSON 형식으로 직렬화 할 수 있다.

[Python Code]

json_string = model.to_json()  # 저장
model = tf.keras.models.model_from_json(json_string)  # 복원

만약 모델의 가중치와 최적화 매개변수를 같이 저장할 경우에는 다음과 같이 .h5 형식으로 저장하면된다.

[Python Code]

model.save('my_model.h5')  # 저장
model = tf.keras.models.load_model('my_model.h5')  # 복원

(6) tf.data.datasets 를 이용한 훈련

텐서플로가 2.x 버전으로 되면서 추가된 또다른 이점은 바로 오디오, 이미지, 비디오, 텍스트, 번역과 같이 다양한 범주에 걸쳐 존재하는 데이터 셋을 처리하도록 하는 datasets 의 도입이다.
사용을 하려면, 먼저 “pip install tensorflow-datasets” 를 설치해야한다. 설치가 완료되면 사용법을 확인하기 위해 아래의 코드를 작성 후 실행한다.

[Python Code]

import tensorflow as tf
import tensorflow_datasets as tfds

builders = tfds.list_builders()
print(builders)

data, info = tfds.load("mnist", with_info=True)
train_data, test_data = data['train'], data['test']

print(info)

[실행 결과]

tfds.core.DatasetInfo(
    name='mnist',
    full_name='mnist/3.0.1',
    description="""
    The MNIST database of handwritten digits.
    """,
    homepage='http://yann.lecun.com/exdb/mnist/',
    data_path='C:\\Users\\slyki\\tensorflow_datasets\\mnist\\3.0.1',
    download_size=11.06 MiB,
    dataset_size=21.00 MiB,
    features=FeaturesDict({
    'image': Image(shape=(28, 28, 1), dtype=tf.uint8),
    'label': ClassLabel(shape=(), dtype=tf.int64, num_classes=10),
}),
supervised_keys=('image', 'label'),
splits={
    'test': <SplitInfo num_examples=10000, num_shards=1>,
    'train': <SplitInfo num_examples=60000, num_shards=1>,
},
citation="""
    @article{
        lecun2010mnist,
        title={MNIST handwritten digit database},
        author={LeCun, Yann and Cortes, Corinna and Burges, CJ},
        journal={ATT Labs [Online]. Available: http://yann.lecun.com/exdb/mnist},
        volume={2},
        year={2010}
    }""",
)

결과 출력까지 약간의 시간이 소요될 수 있으니 참고하기 바란다. 또한 언급하진 않았지만, 이 외에도 케라스와 관련된 추정기나, 비정형 텐서, 맞춤형 훈련 등 2.x 로 버전업이 되면서 추가된 유용한 기능들이 많으니 궁금한 사람은 개별적으로 찾아보기 바란다.

6. 초기 신경망 : 퍼셉트론(Perceptron)

이번 절에서는 앞서 살펴본 keras 를 활용해서 최초의 신경망인 퍼셉트론과 다층 퍼셉트론(MLP, Multi-Layer Perceptron) 을 구현할 예정이다. 구현에 앞서 간단하게 퍼셉트론에 대해 알아보자.

1) 퍼셉트론 (Perceptron)

퍼셉트론은 초기에 단순하게 계산을 위한 두 계층의 인공신경망으로 1950년대 후반에 시작되었고, 1960년대에 다층 퍼셉트론을 훈련시키기 위한 역전파(Back-propagation) 알고리즘이 소개되면서 확장되었다. 특징으로는 n 개의 입력벡터가 주어지면 1(예) 또는 0(아니오)을 출력하는 알고리즘이다. 이를 수학적으로 표현하면 아래와 같다.

$ f(x) = \begin {cases} 1 wx + b > 0 \ 0 \text {그 외} \end {cases} $

위의 수식에서는 w 는 가중치 벡터이고, 이를 입력 데이터 x 와의 점곱, b 는 편향을 의미한다. 기하학에서는 wx+b는 w 와 b 에 할당된 값에 따라 위치를 변경하는 초평면 경계를 정의한 것이라고 볼 수 있다.
이제 위의 내용을 케라스를 활용해서 간단하게 코드로 구현해보자.

[Python Code]

import tensorflow as tf
from tensorflow import keras

CLASSES = 10
RESHAPE = 784

model = tf.keras.models.Sequential()
model.add(keras.layers.Dense(CLASSES, input_shape=(RESHAPE,),
kernel_initializer='zeros', name='dense_layer', activation='softmax'))

print(model.summary())

[실행 결과]

Model: "sequential_1"
_________________________________________________________________
Layer (type)                 Output Shape              Param #
=================================================================
dense_layer (Dense)          (None, 10)                7850
=================================================================
Total params: 7,850
Trainable params: 7,850
Non-trainable params: 0
_________________________________________________________________
None

위의 코드 내용을 잠깐 살펴보면, 먼저 신경망의 각 계층을 순차적으로 생성하기 위해서 models.Sequential() 을 선언해준다. 이 후 모델에 Dense layer 를 add 메소드로 추가해주었고, 이 때 입력 개수는 RESHAPE 에 정의한 수만큼 생성하고, 출력은 CLASSES 에 선언된 값 만큼 출력을 생성한다.
다음으로 확인할 것은 kernel_initalizer 파라미터 인데 이는 특정 가중치로 초기화해주는 파라미터이다. 파라미터 값을 zeros 로 설정했기 때문에 초기 가중치는 모두 0으로 초기화했다는 것을 확인할 수 있다. 마지막으로 출력 계층을 생성하기 위한 활성화 함수로는 소프트맥스 함수를 사용하였다.

2) 다층 퍼셉트론 (MLP, Multi-Layer Perceptron)

퍼셉트론이 여러 개의 층으로 이어져있는 퍼셉트론 모델을 의미하며, 특징으로는 입력과 출력 계층은 외부에서 볼 수 있지만, 중간에 은닉 계층이 존재하며, 이름에서 알 수 있듯이, 숨겨진 층이다. 은닉층의 역할은 각 노드로부터 받은 입력값을 선형함수에 적용해서 나오는 결과를 출력층으로 전달한다.
물론 단일 퍼셉트론 보다 성능은 좋아졌지만, 한가지 문제점이 생긴다. 예를 들어 각 뉴런이 이미지의 단일 픽셀값을 입력으로 받는다고 가정해보자. 앞서 언급한 것처럼 신경망에서는 뉴런의 가중치와 편향을 미세하게 조절함으로 잘못 인식된 이미지의 비율을 감소시키는 것이 목적이다. 매우 직관적으로 보일 수 있지만, 출력에 변화를 주려면, 가중치와 편향 역시 미세하게 조정해야될 필요가 있다. 하지만 퍼셉트론은 0 또는 1을 반환하기 때문에 미세 조정이라는 표현과는 거리가 매우 멀다. 위와 같은 문제점을 해결하기 위해 수학에서의 미분이 도입되며, 미분 가능한 연속적인 함수를 찾게 되는데 이것을 활성화 함수 라고 부른다. 활성화 함수에 대한 내용도 별도로 다룰 내용이므로 이번장에서는 가볍게 정의만 알고 넘어가도록 하자.

7. 실습 : MLP 구현하기

이번에는 단일 퍼셉트론을 활용하여 MLP 를 구현해보도록 하자. 이번 예제에서 사용할 데이터는 Fashion MNIST 데이터로 의류 이미지 분류에 대한 데이터 셋이다. 해당 데이터는 keras 내의 dataset 라이브러리에 있는 fashion_mnist.load_data() 를 사용해서 불러올 수 있다.

[Python Code]

import numpy as np
import pandas as pd

import tensorflow as tf
from tensorflow import keras

from matplotlib import pyplot as plt

# Data Load
fashion_mnist = keras.datasets.fashion_mnist
(x_data, y_data) , (x_test, y_test) = fashion_mnist.load_data()

데이터는 크게 학습용 데이터와 테스트용 데이터로 구분되어 있으며, 학습용은 60,000개, 테스트용은 10,000 개의 데이터가 있다.

[Python Code]

print(x_data.shape)
print(x_data.dtype)
print(x_test.shape)
print(x_test.dtype)

[실행결과]

(60000, 28, 28)
uint8

(10000, 28, 28)
uint8

데이터에서 나타나는 각 라벨에 대한 의류명은 다음과 같다.

[Python Code]

class_names = ['T-shirt/top', 'Trouser', 'Pullover', 'Dress', 'Coat',
    'Sandal', 'Shirt', 'Sneaker', 'Bag', 'Ankle boot']

훈련용 데이터의 경우에는 모델 학습에 대한 검증을 하기 위해 1 ~ 5000 개 까지는 검증용 데이터로, 나머지 55,000 개는 학습에 사용하도록 데이터를 분할한다. 또한 본래 이미지는 RGB의 이미지였지만, 원할한 학습을 하기 위해 Gray-scale 로 변환한다.

[Python Code]

x_valid, x_train = x_data[:5000] / 255.0, x_data[5000:] / 255.0
y_valid, y_train = y_data[:5000], y_data[5000:]
x_test = x_test / 255.0

Gray-scale 로 변환한 결과를 확인하기 위해 아래의 코드를 실행시켜보자.

[Python Code]

plt.figure(figsize=(10,10))
for i in range(25):
    plt.subplot(5,5,i+1)
    plt.xticks([])
    plt.yticks([])
    plt.grid(False)
    plt.imshow(x_train[i], cmap=plt.cm.binary)
    plt.xlabel(class_names[y_train[i]])
    
plt.show()

[실행 결과]

이제 학습을 하기 위한 모델을 생성하자. 구현할 신경망은 입력층 - 은닉층 - 출력층의 3개 층으로 구현된 MLP를 생성할 것이며, keras 의 Sequential API 를 사용해서 생성한다.

[Python Code]

model = keras.Sequential([
    keras.layers.Flatten(input_shape=(28, 28)),
    keras.layers.Dense(128, activation='relu'),
    keras.layers.Dense(10, activation='softmax')
])

Sequential() 은 가장 간단한 신경망 모델이며, 함수 내에 정의한 순서대로 연결된 층을 일렬로 쌓아서 모델을 생성한다. 그 다음으로 등장하는 Flatten() 은 입력으로 들어오는 값을 1차원의 배열로 변환시켜준다. 이 때 입력으로 들어오는 샘플의 크기(배치크기를 제외한 shape) 을 매개변수로 전달해주어야 하며, 이를 reshape(-1, 1) 연산 결과로 전처리한다고 볼 수 있다.
전처리가 완료되면 Dense() 를 사용해 은닉층을 추가한다. Dense 층은 각자 가중치 행렬을 관리하게 되며, 이전 층의 결과와 해당 은닉층 간의 모든 연결 가중치가 포함되고, 각 뉴런마다 존재하는 편향도 별도의 벡터로 관리된다. 구현할 때는 은닉층을 구성할 뉴런의 개수와 결과를 생성할 때, 사용될 활성화함수를 매개변수로 전달한다. 위의 예제에서는 128개 뉴런으로 구성했고, 활성화함수는 ReLU 함수를 사용하였다.
마지막으로 출력층 역시 Dense() 로 구현했으며, 출력되는 결과는 이전에 정의한 labels 의 개수만큼 뉴런을 생성해주면 된다. 또한 최종 결과는 1개의 값으로 생성해야되기 때문에 활성화함수로 SoftMax 함수를 사용하였다.

신경망에 대한 구성을 마치고 나서는 모델을 컴파일 해줘야하는데 이 때, 최적화에 대한 방식을 지정하면된다. 예제에서는 최적화함수로 ADAM 을 사용했고, 학습에 대한 손실을 계산하는 방법은 범주형 변수이기 때문에 Sparse Categorical Crossentropy 함수를 사용한다.
아래부분은 간단하게 설명하면, 모델이 어떻게 학습할 지에 대한 식을 정의하는 부분이라고 이해하면된다. 최적화와 손실함수는 이 후에 다시 살펴볼 예정이므로, 이번 예제에서는 넘어가도록하자.

[Python Code]

model.compile(optimizer='adam',
    loss='sparse_categorical_crossentropy',
    metrics=['accuracy']
)

구성을 완료했으므로, 학습용 데이터를 사용해 모델을 학습하고, 검증용 데이터로 검증해보자.

[Python Code]

# model training
history = model.fit(x_train, y_train, epochs=5)

# model validation
valid_loss, valid_acc = model.evaluate(x_valid,  y_valid, verbose=2)
print('\n테스트 정확도:', valid_acc)

[실행결과]

테스트 정확도: 0.8687999844551086

최종적으로 결과에 대한 시각화는 아래와 같다.

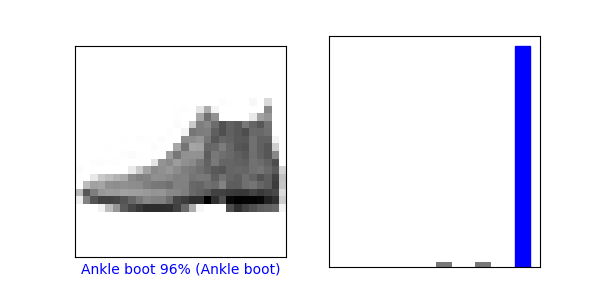
[참고자료]
텐서플로2와 케라스로 구현하는 딥러닝 2/e (에이콘출판사, 안토니오 걸리, 아미타카푸어, 수짓 팔 지음)
텐서플로2와 케라스로 구현하는 딥러닝 2/e